逻辑,属于众多分析难题中最可做的一类,构造则是分析难题中考察面最广的一类。
引子——树上的数
逻辑推理 > 链的部分很可做,考虑构造。
删边会交换,具体为对于任意一个数只会往前交换,对于往后交换过的数不能自主往前交换只能被替交换,一边只能通过一个往前交换的数。
我们需要尽量将较小的编号换到较小的数上,是否依次贪心无后效性,非也,考虑消除,由上知我们仅需考虑较小数另一边的 先交换的情况。
可以写标记处理,以下为具体实现和构造难点扩展。
逻辑推理 > 考虑树,由上推出,需维护共用同一个顶点的边删除的先后关系,性质不变。
此时会发现以上的具体描述阻碍思考,正常,越复杂越难深入,不妨用回原来的定义。
于是,假如我们当前枚举一个数i,去扩展可行的点,记录可以走到的最小的点。对于可走不可走,有三条限制:
1. 不能有边比当前的第一条边先删除;不能有边比当前的最后一条边后删除
2. 一条边不能在存在另一条边紧跟着它被删除的情况下,再出现一条边,也要紧跟着它删除。
3. 如果当前的操作会导致当前的第一条边和最后一条边合并在一条链里面,并且除开它们所在的链以外还有一些链没有合并起来,那么这就是不合法的(参考菊花图,这样会导致边删不完)
可以用数据结构(链表或并查集)维护这些限制。
/*
维护思路:从小到大填数,按照限制寻找
看到图论里面的限制其实一个很自然的想法就是:连边为限制 ,但是这里的限制是针对边的,那么就可以考虑把边转化成点。
对原树上的每一个点建一张图,图上每个点代表连的一条边,并记录这个点钦定的第一条边和最后一条边。这张图上的一条有向边表示出点在入点之后马上选择。点与点之间建的图是独立的。
考虑什么情况下会出现矛盾。
> 图不能被分割成独立的若干条链(这样就会有一条边后面要连多条边,或是出现环,显然不合法)
> 钦定的第一个点和最后一个点有入/出边(显然不合法)
> 第一个点和最后一个点在同一条链上,但是还有点不在这条链中。(已经形成了完备唯一的删边方案,但是有边还没删)
这些条件的矛盾分别表现为:
> 首先是加边的时候两点不能已经连通,这个并查集判一下就好了;然后出点不能有出边,入点不能有入边,bool 数组记录即可。
> 直接判断
> 这条边会让钦定的起点和终点合并,但是目前不连通的个数还大于 2
*/
#include <bits/stdc++.h>
using namespace std;
const int N = 2005;
int n, nump[N];
struct edge
{
int to, next;
} e[N * 2]; // 无向树
int h[N], tot;
struct node // 并查集维护的结点
{
int cnt;
int fst, lst, fa[N];
bool bg[N], ed[N]; // 出边和入边
void clear() {fst = lst = cnt = 0; for (int i = 1; i <= n; i ++ ) fa[i] = i, bg[i] = ed[i] = 1;}
int find(int x) {return fa[x] == x ? x : fa[x] = find(fa[x]);}
} t[N];
inline void add(int a, int b)
{
e[ ++ tot] = {a, h[b]}; h[b] = tot; ++ t[b].cnt;
}
int dfs1(int u, int fe)
{
int res = n + 1;
if (fe && (!t[u].lst || t[u].lst == fe)) {
if (t[u].ed[fe] && !(t[u].fst && t[u].cnt > 1 && t[u].find(fe) == t[u].find(t[u].fst)))
res = u;
}
for (int i = h[u]; i != -1; i = e[i].next)
{
int v = e[i].to, te = (i >> 1);
if (fe == te) continue;
if (!fe)
{
if (!t[u].fst || t[u].fst == te)
{
if (!t[u].bg[te]) continue;
if (t[u].lst && t[u].cnt > 1 && t[u].find(te) == t[u].find(t[u].lst)) continue;
res = min(res, dfs1(v, te));
}
else continue;
}
else
{
if (fe == t[u].lst || te == t[u].fst || t[u].find(fe) == t[u].find(te)) continue;
if (!t[u].ed[fe] || !t[u].bg[te]) continue;
if (t[u].fst && t[u].lst && t[u].cnt > 2 && t[u].find(fe) == t[u].find(t[u].fst) && t[u].find(te) == t[u].find(t[u].lst)) continue;
res = min(res, dfs1(v, te));
}
}
return res;
}
int dfs2(int u, int fe, int p)
{
if (u == p) return t[u].lst = fe, 1;
for (int i = h[u]; i != -1; i = e[i].next)
{
int v = e[i].to, te = (i >> 1);
if (fe == te) continue;
if (dfs2(v, te, p))
{
if (!fe) t[u].fst = te;
else
{
t[u].ed[fe] = t[u].bg[te] = 0; -- t[u].cnt;
t[u].fa[t[u].find(fe)] = t[u].find(te);
}
return 1;
}
}
return 0;
}
int main()
{
int T;
scanf ("%d", &T);
while (T -- )
{
scanf ("%d", &n);
tot = 1;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ ) t[i].clear();
for (int i = 1; i <= n; i ++ ) scanf("%d", &nump[i]);
for (int i = 1; i < n; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
add(a, b), add(b, a);
}
for (int i = 1; i <= n; i ++ )
{
int p = dfs1(nump[i], 0);
dfs2(nump[i], 0, p);
printf("%d ", p);
}
puts("");
}
}
心跳
逻辑推理 > 分析它去掉某个数后前缀和的最大值(对搬运润色)。
设 k 为该数组原先的前缀最大值个数。那么去掉一个数后,
1. 若其原先不是前缀最大值,则前缀最大值个数不变,仍为 k。
2. 若其原先是前缀最大值,则前缀最大值个数先减 1,然后其后有一些本不是前缀最大值上的数将变为前缀最大值,因此还会加上一些数,因此前缀最大值个数变为 [k−1,n] 的某个数。
逻辑推理 > 构造最优方案,对于数组 a,若存在 p 与其对应,则称这些 a 为合法的。我们对于合法的 a,我们先构造一个 p。
直观上,对于合法的 a 唯一对应了一个 k,逻辑(我们需要确定 k)推理假设我们已经知道 k 了。
为了简化分析,我们引入了分类和染色。
接下来,我们开始尝试构造一个 p 与 a 对应。我们将整个过程分为三步:
1.考虑那些不等于 k 的位置 i。若其小于 k−1 是无解的,否则设其为 x,且 x−(k−1)=y。这就要求去掉此位置之后, 有至少 y 个位置会成为新的前缀最大值。为了方便唯一对应,我们就钦定 i 后面的 y 个位置是备用最大值 (⋆)。
2.设在第一步中,我们确定了 w 个位置是前缀最大值,那么还需要钦定 k−w 个等于 k 的位置为前缀最大值。对于这些位置,去掉他们会有 1 个位置成为新的前缀最大值。也就是说,这些位置后面必须跟着一个非前缀最大值的 k。为了方便唯一对应,我们就从前往后扫,每次遇到两个连续的未在第一步中被钦定的数,我们就钦定前一个是前缀最大值,后一个是备用最大值。
3.对于那些既不是前缀最大值,又不是备用最大值的数,就称为垃圾。
我们将前缀最大值染成红色,备用最大值染上绿色,垃圾染上黄色。这样,我们就将一个 aa 序列唯一对应到了一个颜色序列。颜色序列拥有好的性质:
1.一个颜色序列唯一对应了一个 a 序列。
2.对于任意一个颜色序列,都存在排列 p 与之对应。
前者的正确性比较自然,直接根据颜色序列算 a 序列就好。对于后者,我们采取以下的插入构造法得到一个 p。
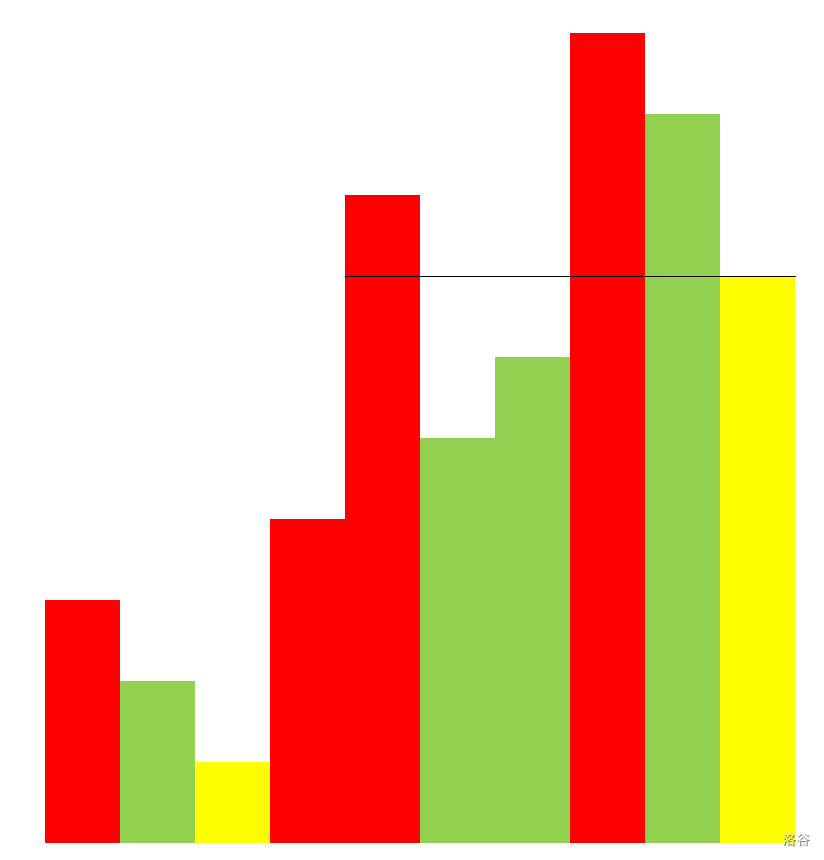
稍微解释一下,绿色位置的值大于上上个红色,小于上个红色,升序排列;黄色位置的值小于上上个红色位置,或者小于上个绿色位置。这样一定是可以构造出来的。
那么现在,我们只需要对颜色序列计数就可以了。我们再来回忆一下先前的构造中隐含的要求,并非所有红黄绿组成的序列都是我们说的颜色序列。颜色序列的要求有哪些呢?
1.绿色(备用最大值)仅应该紧跟着红色(前缀最大值),这是为了满足 (⋆)。
2.“红绿X”段应该尽可能靠前,其中 X 是任意一个非绿的颜色,即“红绿X”不能出现在“黄黄”之后(否则可以把后面的红绿与前面的黄黄交换位置,不满足红绿考前的要求)。“黄红绿X”也不应该出现(因为它可以换成“红绿黄X”)。
3.第一个数一定是红色,第二个数一定不是黄色。后者是因为,去掉第一个数后,第二个数一定成为前缀最大值。
据此,我们就可以根据这三个条件,开始设计关于颜色序列计数的 dp 了。
接下来,我们开始设计状态。考察我们需要记录哪些信息:
前一个是什么颜色。
前面是否有“黄黄”。
这一段绿色段是 0、1 还是大于等于 2。
这一段绿色前面的红色是否在黄色后面。
你可以就根据这四个写,也可以参考这个压缩后的状态:
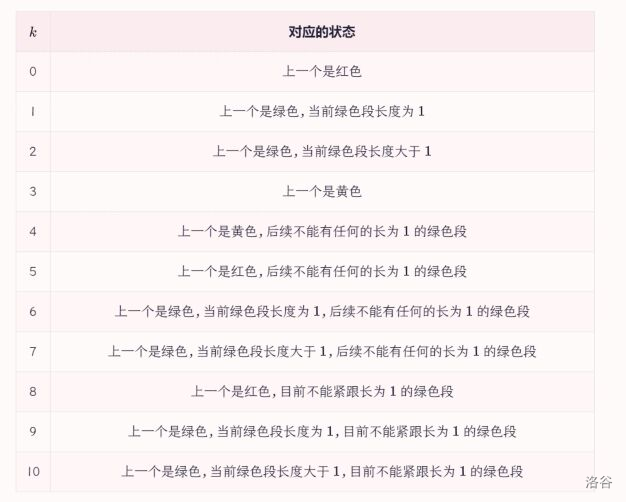
转移待会补。
以上我们只考虑了 m=1,其实 m>1 也有一些讨论的地方。
只需要额外记录两个信息:
1.当前红色的个数。
2.是否有不接绿色的红色。
对于条件 2,我是直接跑了两遍,第二遍跑的时候强制不在红色后面跟红色和黄色。这样方便,合在一起很难写。最后所有数大于等于 m 就是要求此值大于等于 m:红色的个数-[存在不接绿色的红色]。
挑战——醒来
逻辑推理 > 给所有数减去 l∼r 的按位与,因为这些位没有影响。
我们给二进制下 1 个数为奇数的数涂上黑色,其余涂上白色。设 r 的最高位是 p=2q
。
做好准备以后,先来看看两个显然无解的情况:
1.答案排列一定是黑白相间的,所以如果原排列中黑色点的个数与白色点相差了 2 及以上,那寄。
2.如果 l+p>r,那大于等于 p 的和小于 p 的根本连不上。
接下来,先介绍构造的方法,构造的充分性最后说。
1.答案排列可以分为两部分,左边一部分小于 p,右边一部分大于等于 p。
2.若 p−l 是奇数,则选取 l 作为左边部分最后一个数,l+p 作为右边部分第一个数。
否则,选取 r−p 作为左边部分最后一个数,r 作为右边部分第一个数。3.确定好接口以后,只需解决此问题:构造 0∼m 的,以 k 作为一个端点的符合要求的排列。
接下来需要构造构造 0∼M−1 的,0 开头,k 为最后一个元素的排列,类比 格雷码 考虑。

