递推与递归
下节课讲Trie树啦!
递推与递归的思想有点类似分治的思想。
就是每次用以前的数据推导出新的数据。
比如我们熟知的Feb数列(斐波那契数列)。
递推公式为:Fib[i] = Fib[i - 1] + Fib[i - 2];
那我们如何计算公式呢?
举个例子。
大家都知道我多大吧(当我没说)。
小学奥数有种很NB的公式叫做错排公式。
其中一道经典的不能在经典的数学题是这么描述的:
有5只信鸽和5封信。要求每只信鸽不能匹配到与其对应的信(鸽子1对信1……),问有几种可能的情况?
好我们来看一下本题是如何递归的。
第一步:确定C[1]和C[0]是几。
C[0]废话是0,C[1]应该是0。
第二步:通过机智的大脑递推公式。
然后我们就可以开始递推公式啦:
请看下图:
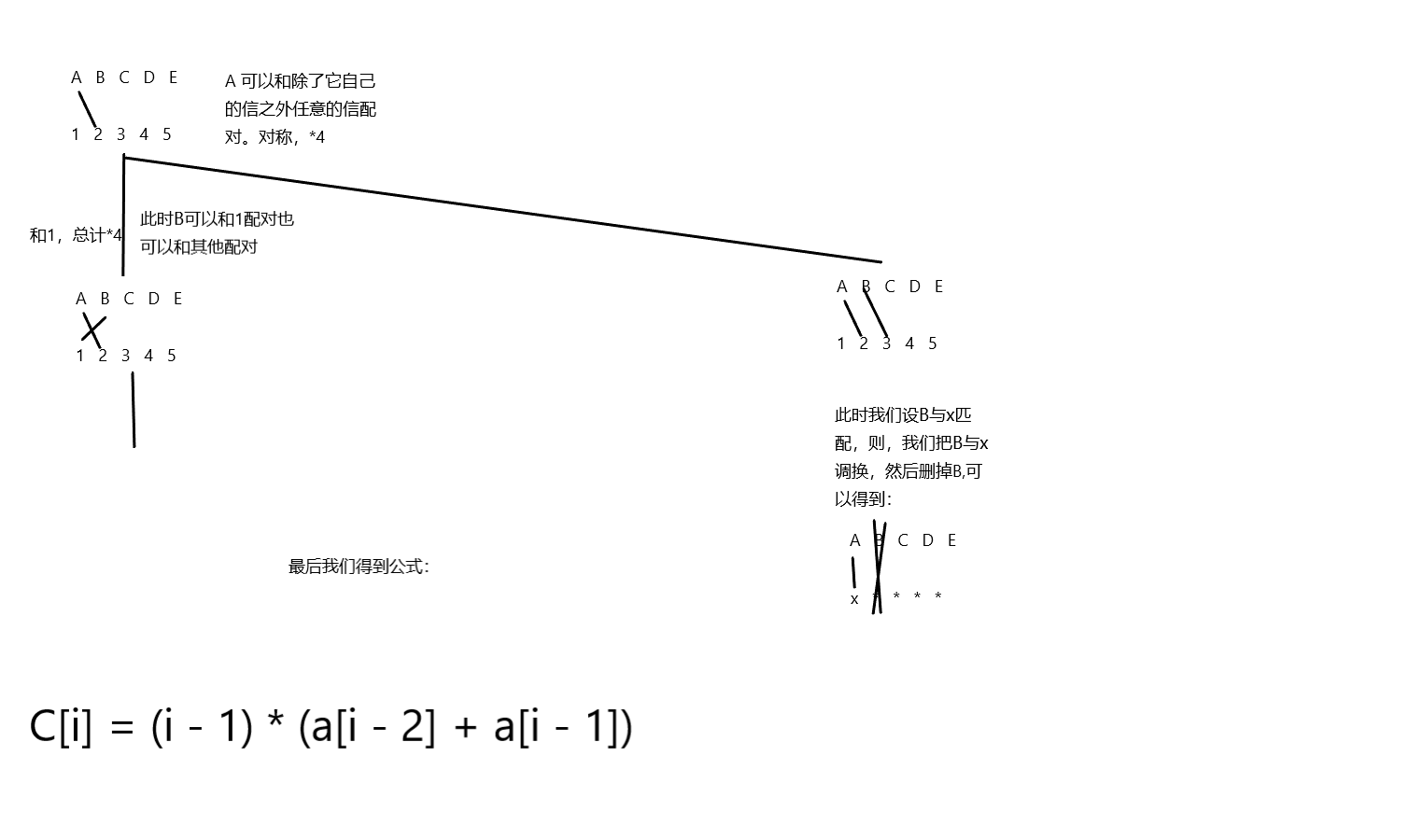
好我们这里用C[i]来表示“i错排”,然后A-E表示鸽子,1-5表示信封。
所以经过一波推倒后,我们得出了公式。
这就是递推。
好接下来留一道作业。
这道作业是大家熟知的小学《迎春杯》比赛原题。
有6个箱子A-F,每个箱子里有一把钥匙,拿到钥匙i就能打开箱子i。现在我们强行打开1,2箱子,取出里面的钥匙,然后用这些钥匙打开其他箱子……最后问有几种可能打开所有箱子。
在这里举一种可以成功打开和不可以成功打开的栗子例子。
可以成功:
箱子:A B C D E F
钥匙:2 3 4 5 6 1
此时我们就可以顺次打开所有箱子。
举一种不可以的栗子:
箱子:A B C D E F
钥匙:2 3 4 5 1 6
好接下来我们继续学习如何用递推解决编程问题。
其实我们的Dp就是从递推延伸而来。
所以来道Dp玩玩:数字三角形欢迎您的光临
本题是Dp中基础中的基础。
好我们看下如何去做这道题目。
首先我画图给大家演示下。
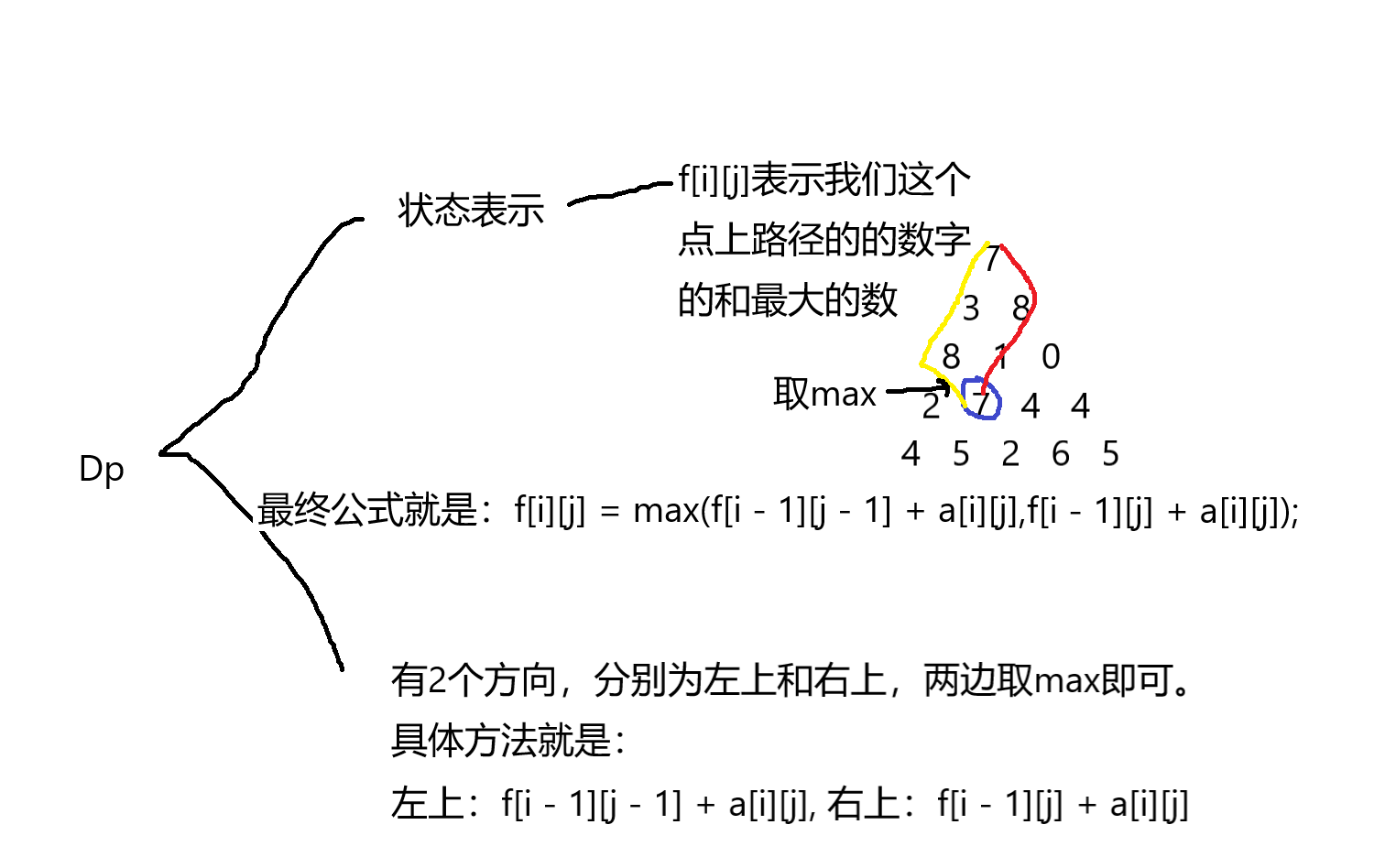
这就是Dp的推导思路。
当然Dp靠的是思想。
就是递推。
所以本题的代码也就显而易见了。
大家先去自己写下在回来~
**
卡住的或者AC的想来继续看看的继续。
本题代码可以分为这几个部分:
第一步:读入a数组。
scanf("%d", &n);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= i; j ++)
scanf("%d", &a[i][j]);
注意Dp我们为了不数组越界所以要从1开始读。
第二步:初始化f数组。
for(int i = 0; i <= n; i ++)
for(int j = 0; j <= i + 1; j ++)
f[i][j] = -INF;
注意这里要全部初始化!!!
第三步:计算f数组,输出。
for(int i = 2; i <= n; i ++)
for(int j = 1; j <= i; j ++)
f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
int res = -INF;
for(int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
cout << res << endl;
return 0;
全部代码有点长,大家分段理解~
#include<iostream>
using namespace std;
const int N = 510, INF = 1e9;
int n, a[N][N], f[N][N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= i; j ++)
scanf("%d", &a[i][j]);
for(int i = 0; i <= n; i ++)
for(int j = 0; j <= i + 1; j ++)
f[i][j] = -INF;
f[1][1] = a[1][1];
for(int i = 2; i <= n; i ++)
for(int j = 1; j <= i; j ++)
f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);
int res = -INF;
for(int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
cout << res << endl;
return 0;
}


在数字三角形这题中,每次状态转移的时候,只需要用到上一层的状态,所以我们可以用滚动数组优化一下空间~
代码如下
空间复杂度2n
然后我们可以通过改变转移顺序再优化掉一层
虽然不会有人这么卡代码如下
NB
好冷,咋没人交作业呢。。
good
这题用递推做不香吗(递推公式)
我爱爆搜
根据题意可知,
(1)如果1、2号箱中其中有一个钥匙是1、2号箱的.有4×2×2=16种情况,并且是循环排列,例如,1号箱是1,2号箱是3,接下来3号箱子就只能是百4,5,6,不能是2.当3号箱度是4时,4号箱就只能是5,6,因此每种情况就有3×2=6种方法.
则共有方法:16×6=96(种).
(2)如果1、2号箱知中的钥匙其中一个也没有是1、2号箱的.
有4×3=12种情况,每种情况有8种方法,例如前面是3,4,如果3号箱是5,那么6就可以在4号箱和5号箱,有2×2=4种;如果3号箱是6,那么5就可以在4号箱和6号箱,有2×2=4;如果3号箱是1或2,也4种,即共4×3=12种.
则共有方法:12×12=144(种)
综合起来就共有方法:96+144=240(种).
这是大型分类讨论的思路,正确!
再想想递推咋做。
咋没人交作业?