2019LeetCode暑期打卡活动 Week 6 滑动窗口、双指针与单调队列/栈

LeetCode 162 两数之和II

考点：双指针算法
双指针 从暴力改成双指针（寻找单调性来优化）

Java

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        if (numbers.length == 2) return new int[]{1, 2};
        for (int i = 0; i < numbers.length; i ++ ) {
            for (int j = 0; j < i; j ++ ) {
                if (numbers[j] + numbers[i] == target) return new int[]{j + 1, i + 1};
            }
        }
        return new int[]{1, 2};
    }
}

j从前面枚举，i从后面枚举
找大于等于target的第一个数

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int j = 0, i = numbers.length - 1; j < numbers.length; j ++ ) {
             // i 和 j 是大于等于target的第一个
            while (i - 1 > j && numbers[i - 1] + numbers[j] >= target) i -- ; 
            if (numbers[i] + numbers[j] == target) return new int[]{j + 1, i + 1};
        }
        return new int[]{1, 2};
    }
}

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int left = 0, right = numbers.length - 1;
        while(left < right) {
            int sum = numbers[left] + numbers[right];
            if (sum > target) {
                right --;
            }else if (sum < target) {
                left ++;
            }else {
                return new int[]{left + 1,right + 1};
            }

        }
        return new int[2];

    }
}

LeetCode 88 合并有序数组

和归并排序是一样的思路，但简化了排序这一步骤，只需要合并
合并可以从最小的一端开始，也可以从最大的一端开始
双指针算法
由于没有新开数组，所以从最大端开始

Java

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m - 1;
        int j = n - 1;
        int k = n + m - 1;

        while (i >= 0  && j >= 0) {
            if (nums1[i] > nums2[j]) nums1[k -- ] = nums1[i -- ];
            else nums1[k -- ] = nums2[j -- ];
        }
        while (j >= 0) nums1[k -- ] = nums2[j -- ];
    }
}

C++

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int i = m - 1, j = n - 1, k = m + n - 1;

        while (j >= 0 && i >= 0)
        {
            if (nums1[i] >= nums2[j]) nums1[k -- ] = nums1[i -- ];
            else nums1[k -- ] = nums2[j -- ];
        }

        while(j >= 0) nums1[k -- ] = nums2[j -- ];

    }
};

26 删除排序数组中的重复元素

[1 1 2] —— [1 2]
两个指针，第一个指针 枚举到哪个数了，第二个指针，存到哪个数了
有序数组中相同的数一定会挨在一起 让指针i和i - 1的值进行比较

Java

class Solution {
    public int removeDuplicates(int[] nums) {
        int k = 1;
        for (int i = 1; i < nums.length; i ++ ) {
            if (nums[i] != nums[i - 1]) nums[k ++ ] = nums[i];
        }
        return k;
    }
}

C++

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        int k = 1;

        for (int i = 1; i < n; i ++ )
        {
            if (nums[i - 1] != nums[i]) nums[k ++ ] = nums[i];
        }

        return k;
    }
};

连续子序列就是子数组 —— 可采用滑动窗口求解,用双指针来维护一个闭区间[left, right]

滑动窗口问题：可以将一部分问题中的嵌套循环转变为一个单循环，因此它可以减少时间复杂度，是查找满足一定条件的连续区间的性质（长度等）的问题， “请找到满足 xx 的最 xx的区间（子串、子数组）的 xx ”这类问题都可以使用该方法进行解决。” 一般在线性结构里，如数组链表栈字符串等

普遍的模板

int left = 0, right = 0;

while (right < s.size()) {`
    // 增大窗口
    window.add(s[right]);


    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
    right++;
}
//对应上面的例题，中间的while条件需要自己去修改，原理是一样的，遇到不符合的条件，就调整窗口大小

本题代码最长连续不重复子序列

Java

public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    int[] a = new int[n];
    for (int i = 0; i < n; i ++ ) {
        a[i] = sc.nextInt();
    }
    HashSet<Integer> set = new HashSet<>();
    int l = 0, r = 0, length = 0;
    while (r < n) {
        while (set.contains(a[r])) {
            set.remove(a[l ++ ]);
        }
        set.add(a[r ++ ]);
        length = Math.max(length, r - l);

    }
    System.out.println(length);
}

C++

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int count[128] = {0};

        int l = 0, r = 0, len = 0;
        while (r < s.length())
        {
            while (count[s[r]] > 0 && l < r) count[s[l ++ ]] -- ;
            count[s[r ++ ]] ++ ;

            len = max(len, r - l);
        }
        return len;
    }
};

易错代码

while (r < s.length())
{            
    count[s[r ++ ]] ++ ;
    # while 循环中的r已经是++ 过后的，所以count永远是小于等于1的；
    while (count[s[r]] > 1 && l < r) count[s[l ++ ]] -- ;

    len = max(len, r - l);
}

LeetCode 76 最小覆盖子串

滑动窗口算法，也可以看作双指针算法，维护两个窗口的边界
先想想暴力做法：一次枚举每个子串，看是否都包含了t的字母
暴力做法：
1. 先枚举终点
2. 从终点开始枚举起点
3. 找到第一次包含的子串后停下来，再走就变长了

如何判断是否包含 用哈希表或者数组记录字母出现的次数

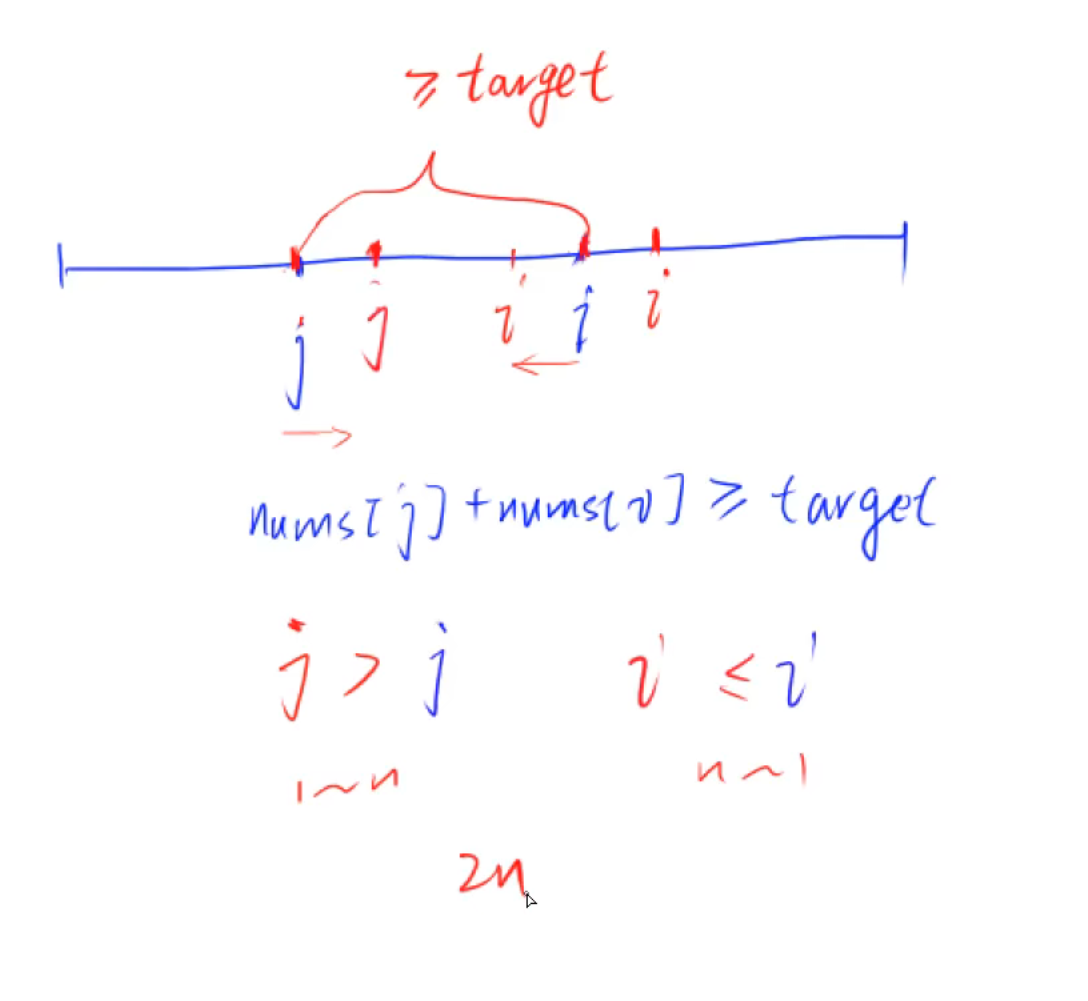
i是自变量，j是因变量，i往后走的过程中，j一定也是不动或者往后走
因为j-i这一段已经包含了，如果i往后走，那么i’-j一定也包含，j’要是在j前面，长度变大了，违背了最小子串
i最多从1-n步 j最多1-n步 时间复杂度o(2n)

题解粘了LeetCode 评论区的代码，无链接

LeetCode 32 最长有效括号

题目分析
括号序列的性质
1. 不管是以哪种角度来看，左括号和它匹配的右括号一定是不变的 )()())
2. 一个括号序列合法 <=> 所有前缀和>= 0 且总和等于0 (左括号为1，右括号为-1)

利用性质来做：
start当前枚举这一段的开头
count 前缀和*从start 加到当前位置(加上当前)
( = 1
) = -1

可能的情况
1. cnt < 0 当前不合法 此时让 start = i + 1, cnt = 0;
2. cnt > 0 当前可能是合法的，继续走
3. cnt = 0 从start到现在所有前缀和大于等于0，且总和等于0 [start, i]是合法的，更新max

上面的做法可以做到右括号大于等于左括号连续的一段，但是可能存在(((()))前缀和一直大于等于0但是总和不等于0，就统计不到了 解决思路：可以再反着做一遍

class Solution {
    public int longestValidParentheses(String s) {
        int res = work(s);
        StringBuilder sb = new StringBuilder(s);
        sb.reverse();
        for (int i = 0; i < s.length(); i ++) {
            char ch = sb.charAt(i);
            if (ch == '(') sb.setCharAt(i, ')');
            else sb.setCharAt(i, '(');
        }
        System.out.println(sb.toString());
        return Math.max(res, work(sb.toString()));

    }
    public int work(String s) {
        int res = 0;
        for (int i = 0, start = 0, cnt = 0; i < s.length(); i ++ ) {
            if (s.charAt(i) == '(') cnt ++ ;
            else {
                cnt -- ;
                if (cnt < 0) {
                    start = i + 1;
                    cnt = 0;
                } else if (cnt == 0) res = Math.max(res, i - start + 1);
            }
        }
        return res;
    }

}

方法二 用栈做
参考小呆呆，粘过来了

1、若当前栈为空 或者 当前元素是’(‘，则直接加入栈中
2、当当前元素是’)’时，说明有和栈顶元素匹配的可能
1、若栈顶元素能和’)’匹配，直接将栈顶元素pop出，则当前元素i与pop元素后的栈顶元素之间的长度是以i结尾的最长有效括号的长度
2、若栈顶元素不能和’)’匹配，则直接加入到栈中
注意：栈保存的是坐标

class Solution {
    public int longestValidParentheses(String s) {
        Stack<Integer> stk = new Stack<Integer>();
        int ans = 0;
        for(int i = 0;i < s.length();i ++)
        {
            char t = s.charAt(i);
            if(stk.isEmpty() || t == '(') stk.add(i);
            else
            {
                if(s.charAt(stk.peek()) == '(') 
                {
                    stk.pop();
                    if(!stk.isEmpty()) ans = Math.max(ans,i - stk.peek());
                    else ans = Math.max(ans,i + 1);
                }
                else stk.add(i);
            }
        }
        return ans;
    }
}

作者：小呆呆
链接：https://www.acwing.com/solution/content/4177/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

LeetCode 155 最小栈

类似于前缀“和”
前缀最值，或者历史最值，所以无需优化

class MinStack {
    Stack<Integer> stk = new Stack<>();
    Stack<Integer> stk_min = new Stack<>(); 
    public MinStack() {

    }

    public void push(int val) {
        stk.push(val);
        if (stk_min.isEmpty()) stk_min.push(val);
        else stk_min.push(Math.min(stk_min.peek(), val));
    }

    public void pop() {
        stk_min.pop();
        stk.pop();
    }

    public int top() {
        return stk.peek();
    }

    public int getMin() {
        return stk_min.peek();
    }
}

单调队列和单调栈的使用场景 看到类似场景直接用下面俩数据结构

单调栈：查找每个数左侧第一个比它小的数
插入的时候，删除完冗余元素后的栈顶元素是我们需要找的数
每个元素进栈一次出栈一次，复杂度是O(n)

单调队列 = 滑动窗口中的最值
如果单调队列是单调下降的，那么队头一定是最大值

LeetCode 42 接雨水

把大佬的题解粘过来了，太优美了

算法1

(三次线性扫描)O(n)

1. 观察整个图形，考虑对水的面积按 列 进行拆解
2. 注意到，每个矩形条上方所能接受的水的高度，是由它左边 最高的 矩形，和右边 最高的 矩形决定的。具体地，假设第 i 个矩形条的高度为height[i]，且矩形条左边 最高的 矩形条的高度为 left_max[i]，右边 最高的 矩形条高度为 right_max[i]，则该矩形条上方能接受水的高度为 min(left_max[i], right_max[i]) - height[i]。
3. 需要分别从左向右扫描求 left_max，从右向左求 right_max，最后统计答案即可。
4. 注意特判 n为0。

时间复杂度
三次线性扫描，故只需要 O(n) 的时间。
空间复杂度
需要额外 O(n) 的空间记录每个位置左边最高的高度和右边最高的高度。
C++ 代码

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size(), ans = 0;
        if (n == 0)
            return 0;

        vector<int> left_max(n), right_max(n);

        left_max[0] = height[0];
        for (int i = 1; i < n; i++) 
            left_max[i] = max(left_max[i - 1], height[i]);

        right_max[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i--)
            right_max[i] = max(right_max[i + 1], height[i]);

        for (int i = 0; i < n; i++)
            ans += min(left_max[i], right_max[i]) - height[i];

        return ans;
    }
};

Java代码

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        if (n == 0) return 0;
        int[] left_max = new int[n];
        int[] right_max = new int[n];

        left_max[0] = height[0];
        for (int i = 1; i < n; i ++ ){
            left_max[i] = Math.max(left_max[i - 1], height[i]);
        }

        right_max[n - 1] = height[n - 1];
        for (int i = n - 2; i >= 0; i -- ) {
            right_max[i] = Math.max(right_max[i + 1], height[i]);
        }

        int res = 0;
        for (int i = 0; i < n; i ++ ) {
            res += Math.min(left_max[i], right_max[i]) - height[i];
        }
        return res;
    }
}

算法2

(单调栈) O(n)

换一种思路，考虑每个位置左边和右边 第一个 比自身不低的矩形条，以及三个矩形条构成的 U 型，相当于对水的面积按 行 进行拆解。
维护严格单调递减的单调栈。在每次检查栈顶要出栈时，i 为右边第一个比 st.top() 不低的矩形，st.top() 弹出栈顶，并将其记为 top。
假设此时栈中仍然存在矩形，现在 st.top()（弹栈后的栈顶）、top 与 i 三个位置构成一个 U 型，其中 top 位置代表 U 型的底部，此时可以计算出该 U 型所能接受的水的面积为 (i - st.top() - 1) * (min(height[st.top()], height[i]) - height[top])。
最后当前矩形进栈。
时间复杂度
每个元素最多进栈一次出栈一次，故只需要 O(n) 的时间。
空间复杂度
需要额外 O(n)的空间存储单调栈。

C++ 代码

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size(), ans = 0;
        stack<int> st;
        for (int i = 0; i < n; i++) {
            while (!st.empty() && height[st.top()] <= height[i]) {
                int top = st.top();
                st.pop();
                if (st.empty()) break;
                ans += (i - st.top() - 1) 
                        * (min(height[st.top()], height[i]) - height[top]);
            }
            st.push(i);
        }
        return ans;
    }
};

Java代码

class Solution {
    public int trap(int[] height) {
        int res = 0;
        Stack<Integer> stk = new Stack<>();

        for (int i = 0; i < height.length; i ++ ) {
            int last = 0;
            while (!stk.isEmpty() && height[stk.peek()] <= height[i]) {
                int t = stk.pop();
                res += (i - t - 1) * (height[t] - last);
                last = height[t];
            }
            if (!stk.isEmpty()) res += (i - stk.peek() - 1) * (height[i] - last);
            stk.push(i);
        }
        return res;

    }
}

作者：wzc1995
链接：https://www.acwing.com/solution/content/121/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

LeetCode 84 柱状图总最大矩形

最大矩形 如何枚举所有的矩形？
底边确定的，高度和宽度不确定
1. 枚举所有柱形的上边界为矩形的上边界
2. 然后求出该上边界能有的左右边界

如何快速求出左右边界？
1. 左边界：左边最近的第一个高度比它小的柱形，
2. 右边界 右边最近的第一个高度比它小的柱形

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        Stack<Integer> stk = new Stack<>();
        int[] left = new int[n + 1];
        int[] right = new int[n + 1];

        for (int i = 0; i < n; i ++ ) {
            while (!stk.isEmpty() &&heights[stk.peek()] >= heights[i]) stk.pop();
            if (stk.isEmpty()) left[i] = -1;
            else left[i] = stk.peek();

            stk.push(i);
        }
        while (!stk.isEmpty()) stk.pop();
        for (int i = n - 1; i >= 0; i --) {
            while (!stk.isEmpty() && heights[stk.peek()] >= heights[i]) stk.pop();
            if (stk.isEmpty()) right[i] = n;
            else right[i] = stk.peek();

            stk.push(i);
        }

        int res = 0;
        for (int i = 0; i < n; i ++ ) {
            res = Math.max(res, (right[i] - left[i] - 1) * heights[i]);
        }
        return res;
    }
}

方案二：
当栈顶元素大于要入栈的元素时，此时的栈顶元素已经可以拥有左右两边的最近的比它小的了
假设当前栈顶为cur，它大于待压入的i
我们弹出cur，i是右边第一个比它小的，弹出cur后的栈顶是左边第一个比它小的

class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = 0;
        int n = heights.length;
        Stack<Integer> stk = new Stack<>();
        //  heights.push_back(-1);
        // 为了算法书写方便，在数组末尾添加高度 -1
        // 这会使得栈中所有数字在最后出栈。
        int h = 0;
        for (int i = 0; i <= n; i ++ ) {
            if (i == n) h = -1;
            else h = heights[i];
            while (!stk.isEmpty() && heights[stk.peek()] > h) {
                int cur = stk.pop();
                int right = i;
                int left = stk.isEmpty() ? 0 : stk.peek() + 1;
                res = Math.max(res, (right - left) * heights[cur]);
            }
            stk.push(i);
        }
        return res;
    }
}

LeetCode 239 滑动窗口最大值

单调队列 = 滑动窗口中的最值
如果单调队列是单调下降的，那么队头一定是最大值

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        List<Integer> res = new ArrayList<>();

        Deque<Integer> q = new ArrayDeque<>();
        for (int i = 0; i < nums.length; i ++ ) {
            if (!q.isEmpty() && i - k + 1 > q.peekFirst()) q.pollFirst(); // 判断单调队列队头是否出列
            while (!q.isEmpty() && nums[q.peekLast()] <= nums[i]) q.pollLast(); // 维护单调性
            q.offerLast(i); // 入队
            if (i >= k - 1) res.add(nums[q.peekFirst()]); // 输出答案
        }
        int n = res.size();
        int[] ans = new int[n];
        for (int i = 0; i < n; i ++ ) {
            ans[i] = res.get(i);
        }
        return ans;
    }
}

LeetCode 918 环形数组最大和

环形问题，可以把环展成链状，环形时是n，链状时是2n
环形所有区间，我们都可以在2n中找，只要我们限定住区间长度不超过n就不会重复元素
所有长度大于等于0 小于等于n的区间最大值，用前缀和

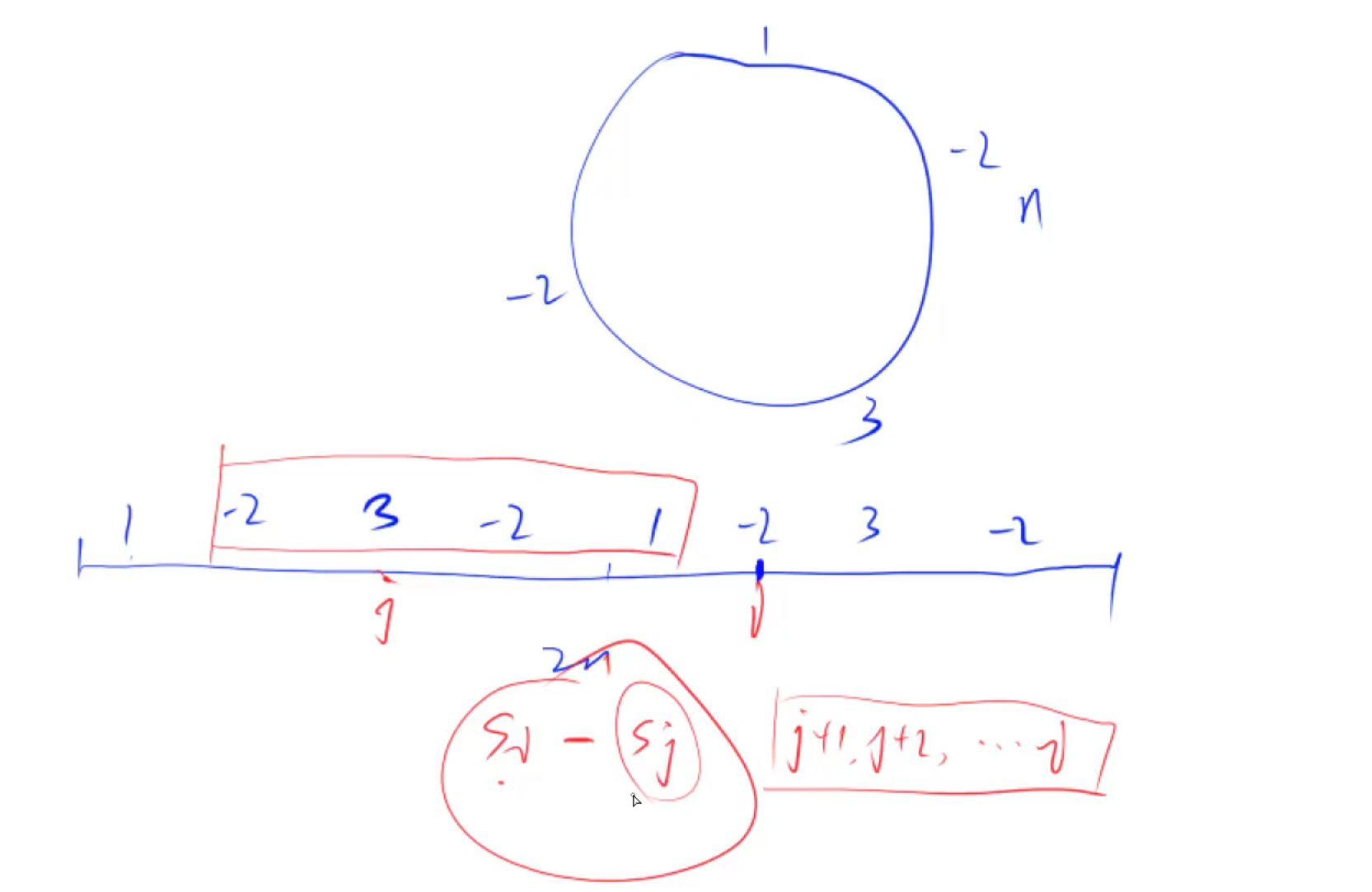
我们先固定i，从i往前n个数的区间内[i, j] 看j + 1, j + 2, j + 3,…, i 之间的最大值
即 s[i] - s[j]的最大值，s[i]已知了，我们需要找最小的s[j]
或者说是窗口[i, j]之前的最大和

class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        int n = nums.length;
        int[] a = new int[n * 2];
        for (int i = 0; i < 2 * n; i ++ ) a[i] = nums[i % n];
        int[] sum = new int[n * 2 + 1];
        for (int i = 1; i < n * 2; i ++ ) sum[i] = sum[i - 1] + a[i - 1];

        int res = Integer.MIN_VALUE;
        Deque<Integer> q = new ArrayDeque<>();
        q.offerLast(0);
        for (int i = 1; i < n * 2; i ++ ) {
            if (!q.isEmpty() && i - n > q.peekFirst()) q.pollFirst();
            if (!q.isEmpty()) res = Math.max(res, sum[i] - sum[q.peekFirst()]);
            while (!q.isEmpty() && sum[i] <= sum[q.peekLast()]) q.pollLast();
            q.offerLast(i);
        }
        return res;
    }
}