Splay 的相关概念

Splay： Splay 是平衡树的一种，和红黑树、treap、AVL 等类似。相比于其他平衡树，Splay 的代码适中，但是非常灵活，能实现很多的操作，有些操作对于别的平衡树来说，可能很难实现或不能实现。

Splay 的应用场景

可以处理序列翻转一类的问题，也可以处理有关于线段的一系列问题，可以处理很多线段树要处理的问题，而且比线段树更灵活。

Splay 的原理

Splay 是一个平衡二叉树，期望是一个 $logn$ 的高度，但是并没有那么平衡。

对于平衡树，会有一个右旋和左旋的操作。

左旋： 对 x 节点左旋，以 x 的右子节点 y 为轴，将 x 转下来变成 y 的左子节点

右旋： 对 y 节点右旋，以 y 的左子节点 x 为轴，将 y 转下来变成 x 的右子节点

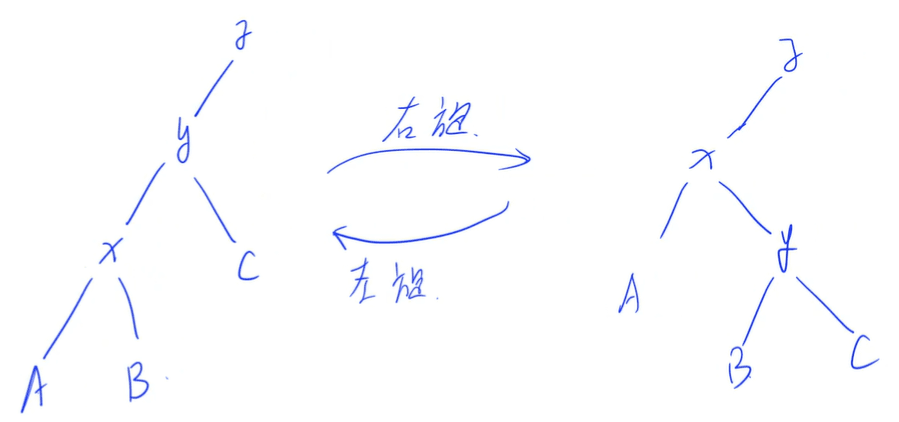
左旋和右旋就是在保证平衡树中序遍历不变的情况下，来动态改变树的高度。

在 Splay 进行任何操作时，不管是插入还是查询等等，我们都将这个点旋转到树根，同时保证中序遍历是不变的。

因此 Splay 的核心思路就是，我们每操作一个节点，都会把这个节点旋转到树根。

这个核心思路是根据局部性原理得出的，意思就是我们当前用到了一个节点，那么在之后的操作中我们还有可能再次用到这个节点。这是一个类似于缓存的思想。通过这个思想，我们能让 Splay 不管在什么样的数据中，都可以做到平均意义下每次操作的时间复杂度是 $O(logn)$ 的。这个平均意义下的时间复杂度是存在严格证明的，可以自行了解。

那么每次操作一个节点时，Splay 是如何将它旋转到树根的呢？

首先我们定义一个函数 $splay(x, k)$，可以把某个点 $x$ 旋转到 $k$ 的下面。如果 $k = 0$，则表示将 $x$ 旋转到根。这是 Splay 的一个核心函数。

要想实现这个函数，我们需要分成两类情况来处理，一类情况是 $x$ 是 $y$ 的左子节点，$y$ 是 $z$ 的左子节点，三个节点呈一条链，另一类情况是 $x$ 是 $y$ 的右子节点， $y$ 是 $z$ 的左子节点，在链的中间会折一下。这两类情况又分别有一个对称情况，一共是两大类四小种。

对于第一类情况，我们先将 $y$ 向上转，再将 $x$ 向上转，这样就能把 $x$ 放到三个节点的最上面。对于第二种情况，我们就先将 $x$ 向上转，再将 $x$ 向上转，同理又能把 $x$ 放到三个节点的最上面。

可以发现，每进行一次以上的操作，我们就能让 $x$ 向上走两层，直到走到某一个点的下面为止，这就是 $splay(x, k)$ 函数的核心原理

有了 Splay 的核心函数 $splay(x, k)$ 后，其他所有操作都是能围绕这个核心函数来实现。

Splay 实现的操作

插入

单纯插入一个数值 $x$，那么我们要找到它应该插入的位置，插入进去后再把它转到根。

将一个序列插入到 $y$ 的后面，我们可以先找到 $y$ 的后继 $z$，接下来就需要在 $y$ 和 $z$ 的中间插入一个序列，我们先将 $y$ 转到根，再把 $z$ 转到 $y$ 的下面，此时由于 $z$ 是 $y$ 的后继，所以 $z$ 一定是 $y$ 的右子节点，且 $z$ 的左子树上一定是空的，那么我们要想将序列插入 $y$ 和 $z$ 之间，其实就是要插入 $z$ 的左子树上，所以我们先将序列构造成一个二叉树，然后直接插到 $z$ 的左子树上即可。

删除

将一段序列 $[L, R]$ 从平衡树中删除，我们找到 $L$ 的前驱 $L-1$ 和 $R$ 的后继 $R+1$，将 $L-1$ 转到根节点，将 $R+1$ 转到根节点的下面，此时 $R+1$ 的左子树就是 $[L, R]$ 这一段序列，直接将整个左子树去掉即可。

维护信息

对于 Splay 来说，需要维护的信息有很多种，根据题目要求来进行定义，除了题目要求的信息以外，如果我们要进行区间修改操作，那么就需要和线段树一样维护一个懒标记，同样需要 $pushup()$ 和 $pushdown()$ 两个函数，$pushup()$ 可以用两个子节点来得到当前节点的信息，$pushdown()$ 则是将当前节点的懒标记传递到两个子节点中。两个函数根据它们的作用分别放在旋转之后以及递归之前。

而对于平衡树来说，一个常用的操作就是找前驱和找后继，对于每个节点，我们可以记录它的两个子节点和父节点，通过子节点和父节点的信息来找前驱和后继。

另外，由于维护信息的过程中可能进行各种各样的操作，使得平衡树中节点的位置发生改变，但是 Splay 能时刻保证中序遍历就是当前序列的顺序，这是 Splay 的特性。