一、前缀和简介

前缀和是一种能够在$O(n)$的预处理，$O(1)$的查询每段区间的和的一个算法。
考试中，前缀和是一种能够降低复杂度的好东西。

二、前缀和算法原理

思路

我们用数组$s$，是的每一个$s_i$都满足$s_i=s_{i-1}+a_i$。
也就是说，$s$数组的每一个位置$i$都表示前$i$个数的和，故叫前缀和。
但是我们要求一段区间的和该怎么办呢？
其实可以用减去多余的部分来求出答案。
比如我们要求区间$[l,r]$的和，假设我们已经算好$s$数组了。
我们先看一张图：

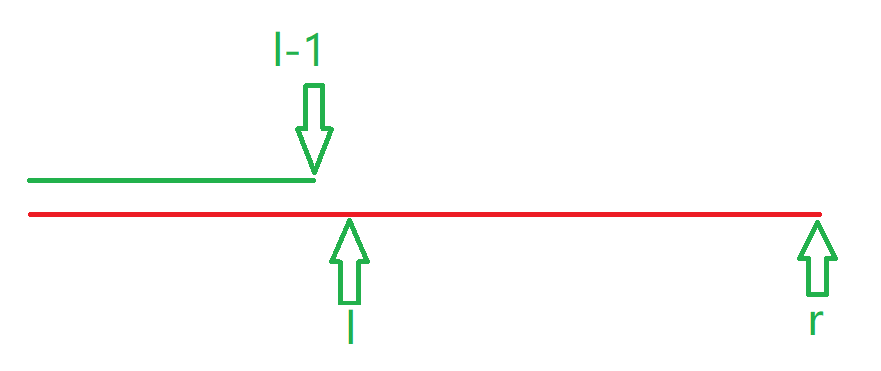
这里我们的和只要红色部分减去绿色部分，红色部分是$s_r$，绿色部分是$s_{l-1}$，所以$sum_{l,r}=s_r-s_{l-1}$。

代码

#include <iostream>
using namespace std;
const int N = 100010;
int n,m;
int a[N];
int s[N];
int main () {
    cin >> n >> m;
    for (int i = 1;i <= n;i++) {
        cin >> a[i];
        s[i] = s[i - 1] + a[i];
    }
    while (m--) {
        int l,r;
        cin >> l >> r;
        cout << s[r] - s[l - 1] << endl;
    }
    return 0;
}

思路

这里我们讲一下二维前缀和。
我们用$s_{i,j}$表示$(i,j)$左上角的所有点（包括他自己）的和。
那我们该怎么求$s$数组呢？
先看一张图：

这里的$s_{i,j}$就是绿色部分$+$蓝色部分$-$紫色部分$+$当前数。
所以$s_{i,j}=s_{i-1,j}+s_{i,j-1}-s_{i-1,j-1}+a_{i,j}$。
那我们要求任意一个部分的和该怎么求呢？
其实也很简单，我们对着上面那的图，就是把蓝色紫色绿色部分的位置改一下。
比如我们要求$(x_1,y_1)$到$(x_2,y_2)$的和，那么这一段的和就是$s_{x_2,y_2}-s_{x_1-1,y_2}-s{x_2,y_1-1}+s_{x_1-1,y_1-1}$

代码

#include <iostream>
using namespace std;
const int N = 1010;
int n,m;
int a[N][N];
int s[N][N];
int main () {
    cin >> n >> m;
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= n;j++) {
            cin >> a[i][j];
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    }
    while (m--) {
        int x1,y1,x2,y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] << endl;
    }
    return 0;
}