事情的起因是这样的：
1254. 统计封闭岛屿的数目
做这道题的时候，被dfs边界卡的一愣一愣的，改了一个多小时，最后终于调出来了。
于是我选择用三种方法对其鞭shi：)

前置知识：
最典型的flood fill模板，究其根本就是用dfs求连通块的数量
200. 岛屿数量

class Solution {
public:
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
    int n,m;
    void dfs(int x,int y,vector<vector<char>>&g)
    {
        g[x][y]='0';
        for(int i=0;i<4;i++)
        {
            int a=dx[i]+x,b=dy[i]+y;
            if(a<0||a>=n||b<0||b>=m)continue;
            if(g[a][b]=='0')continue;
            g[a][b]='0';
            dfs(a,b,g);
        }
    }
    int numIslands(vector<vector<char>>& g) {
        n=g.size(),m=g[0].size();
        int res=0;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                if(g[i][j]=='1')dfs(i,j,g),res++;
        return res;
    }
};

回到本题

1254. 统计封闭岛屿的数目
题目大意：
二维矩阵 grid由 0（土地）和 1（水）组成。岛是由最大的4个方向连通的 0组成的群，封闭岛是一个完全 由1包围（左、上、右、下）的岛。
请返回 封闭岛屿 的数目。
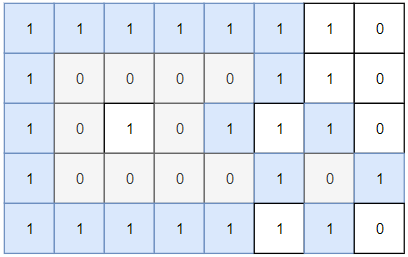
输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：
灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

思路：
统计不连接边界的土地连通块数量即可。
那么求连通块就有三种方法：
1. dfs 2. bfs 3. 并查集

dfs解法

由于这里写的是bool型的dfs并且结果与连通块的数量有关，所以一定要注意每次遍历要遍历完整个连通块，
如果在成短路会对答案造成影响。

class Solution {
public:
    int n,m;
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
    bool dfs(int x,int y,vector<vector<int>>&g)
    {
        if(x<0||x>=n||y<0||y>=m)return false;//--->这两句与注释掉的两句可以互换，
        if(g[x][y])return true;//--->只不过放在这里可以将第一个点也计算到
        g[x][y]=1;
        bool f=false;
        for(int i=0;i<4;i++)
        {
            int a=dx[i]+x,b=dy[i]+y;
            //if(a<0||a>=n||b<0||b>=m)return false;//叶子结点短路无所谓
            //if(g[a][b])continue;
            if(!dfs(a,b,g))f=true;//这里不能直接return false;否则会构成更多的连通块
        }
        if(!f)return true;
        return false;
    }
    int closedIsland(vector<vector<int>>& g) {
        n=g.size(),m=g[0].size();
        int res=0;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                if(g[i][j]==0)
                {
                    if(i==0||i==n-1||j==0||j==m-1)continue;
                    if(dfs(i,j,g))res++;
                }
        return res;
    }
};

bfs解法

bfs解法就相对温和，不需要注意那么多细节

typedef pair<int,int>PII;
class Solution {
public:
    int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
    int n,m;
    bool bfs(int x,int y,vector<vector<int>>&g)
    {
        queue<PII>q;
        q.push({x,y});
        g[x][y]=1;
        bool f=false;
        while(q.size())
        {
            auto t=q.front();
            q.pop();
            for(int i=0;i<4;i++)
            {
                int a=t.first+dx[i],b=dy[i]+t.second;
                if(a<0||a>=n||b<0||b>=m)continue;
                if(g[a][b])continue;
                g[a][b]=1;
                if(a==0||a==n-1||b==0||b==m-1)f=true;//这里也是防止短路
                q.push({a,b});
            }
        }
        if(!f)return true;
        return false;
    }
    int closedIsland(vector<vector<int>>& g) {
        n=g.size(),m=g[0].size();
        int res=0;
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                if(i&&i!=n-1&&j&&j!=m-1&&g[i][j]==0&&bfs(i,j,g))res++,cout<<i<<' '<<j<<endl;
        return res;
    }
};

并查集解法

将所有陆地连通块合并成几个集合，并且对与边缘相连的连通块的祖宗节点进行标记，最后遍历所有集合的祖宗节点，
查看是否被”感染“，计数即可

class Solution {
public:
    int n,m;
    vector<int>f;
    vector<bool>st;
    int find(int x)
    {
        if(x!=f[x])f[x]=find(f[x]);
        return f[x];
    }
    void unite(int x,int y)
    {
        int a=find(x),b=find(y);
        st[a]=st[a]||st[b];//传染
        if(a!=b)f[b]=a;
    }
    int get_idx(int x,int y)
    {
        return x*m+y;
    }
    int closedIsland(vector<vector<int>>& g) {
        n=g.size(),m=g[0].size();
        f.resize(n*m+1);
        st.resize(n*m+1,false);
        for(int i=0;i<n*m;i++)f[i]=i;

        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                if(g[i][j]==0)
                {
                    if(i==0||i==n-1||j==0||j==m-1)st[get_idx(i,j)]=true;
                    if(j>0&&g[i][j]==g[i][j-1])unite(get_idx(i,j),get_idx(i,j-1));
                    if(i>0&&g[i][j]==g[i-1][j])unite(get_idx(i,j),get_idx(i-1,j));
                }
            }
        }

        int res=0;
        for(int i=0;i<n*m;i++)
            if(g[i/m][i%m]==0&&find(i)==i&&!st[find(i)])res++;
        return res;
    }
};