第14章 基础算法与数据结构
1029. Median
笔记
- 先用归并排序的知识合并两个有序段
- 题目定义的偶数个数的中位数为靠左,因此中文数索引为⌊m+n−12⌋
#include <iostream>
using namespace std;
const int N = 2e5 + 10, M = 4e5 + 10;
int a[N], b[N], c[M];
void merge(int a[], int m, int b[], int n) {
int i = 0, j = 0, k = 0;
while(i < m && j < n)
if (a[i] < b[j]) c[k++] = a[i++];
else c[k++] = b[j++];
while(i < m) c[k++] = a[i++];
while(j < n) c[k++] = b[j++];
}
int main() {
int m, n;
scanf("%d", &m);
for (int i = 0; i < m; i++) scanf("%d", &a[i]);
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &b[i]);
merge(a, m, b, n);
int res = c[(m + n - 1) / 2];
printf("%d", res);
return 0;
}
1046. Shortest Distance
笔记
-
由于是环,因此距离分为两种情况,考虑点vl到点vr的距离,由于对称性,不妨设l⩽
- D_l+D_{l+1}+\cdots + D_{r-1}
- (D_1+D_{2}+\cdots + D_{l-1})+(D_r+ D_{r+1} +\dots + D_{N})
-
两者取最小即可得到最小距离
- 可采用前缀和进一步优化表达式
- S_{r-1}-S_{l-1}
- S_{l-1}+(S_N-S_{r-1})
#include <iostream>
#include <cmath>
using namespace std;
const int N = 1e5 + 10;
int n, x, s[N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> x;
s[i] = s[i - 1] + x;
}
int m, l, r;
cin >> m;
while(m--) {
cin >> l >> r;
if (l > r) swap(l, r);
cout << min(s[r - 1] - s[l - 1], s[l - 1] + s[n] - s[r - 1]) << endl;
}
return 0;
}
1085. Perfect Sequence
笔记
- 所有可能序列有2^n种,分析发现,序列排序后,问题就变成:在所有的子区间找满足条件M \leqslant m \times p,且区间元素个数尽可能多的区间,此时搜索范围优化到\frac{n^2}{2}
- 当区间右端点M一定时,区间左端点m越小,区间元素个数越多,因此可从所有元素的最小值开始向右寻找第一个满足M \leqslant m \times p的元素,作为当前M对应的最优m
-
当右端点M_1变为M_2后,为了更快寻找M_2对应的最优m_2,可进一步分析
- 由于m_1是M_1对应的最优解,因此一定有M_1 \leqslant m_1 \times p,此时有可能取到等号
- 由于是从小到大枚举M,因此有M_1 \lt M_2
- 假设m_2 < m_1,及需要回头寻找最优解,则推出M_1 < M_2 \leqslant m_2 \times p \lt m_1 \times p,于是M_1 \lt m_1 \times p,不等式没法取到等号,说明m_1不是首个满足M_1 \leqslant m_1 \times p的情况,即m_1不是M_1的最优解,矛盾
- 综上所述,m_2 \geqslant m_1,所以在确定M_1的最优m_1后,可直接从m_1右边寻找M_2对应的最优m_2
-
基于上述特性,可采用第一类双指针算法,将时间复杂度优化成O(n)
- 排序数组
- 首先用第一个指针枚举所有右端点,然后用第二个指针穷举所有左端点,开始都指向最小的元素
- 右段点指针固定时,让左端点指针向右遍历,直到遇到首个满足M \leqslant m \times p的左端点,更新全局最优解,并右端点指针移到下一个元素,左端点指针不变
- 输出全局最优解
-
其它细节
while条件不需要越界判断,因为m不超过M,因此m \times p最后一定\geqslant M,即m取到M时一定有M \times p \geqslant M,此时条件永假,左端点指针不会继续右移- 由于每个数的取值范围都是
int的表示范围,故在计算m \times p时会超出int的表示范围,故需要把m强制转换成long long类型后再比较
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, p, a[N];
int main() {
cin >> n >> p;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
int res = 0, m, M;
for (int i = 0, j = 0; i < n; i++) {
// 双指针,i表示右端点下标,j表示左端点下标
M = a[i];
m = a[j];
while(M > (long long)m * p) m = a[++j];
res = max(res, i - j + 1);
}
cout << res << endl;
return 0;
}
1091. Acute Stroke
笔记
- 本质是找满足指定结点个数的连通块,并计算这些连通块的总结点个数
- 可用DFS或BFS找连通块,由于PAT的栈空间设置为1MB,因此直接使用DFS会出错,因此本题采用BFS,时间复杂度为O(n)
#include <iostream>
#include <queue>
using namespace std;
const int M = 1292, N = 132, L = 64;
int m, n, l, t;
int st[L][M][N];
struct Node {
int x, y, z;
};
int d[][3] = {
{1, 0, 0},
{-1, 0, 0},
{0, 1, 0},
{0, -1, 0},
{0, 0, 1},
{0, 0, -1}
};
int bfs(int a, int b, int c) {
queue<Node> q;
q.push({a, b, c});
st[a][b][c] = 0;
int cnt = 1;
while(q.size()) {
Node node = q.front();
q.pop();
int u = node.x, v = node.y, w = node.z;
for (int k = 0; k < 6; k++) {
int x = u + d[k][0], y = v + d[k][1], z = w + d[k][2];
if (x >= 0 && x < l && y >= 0 && y < m && z >= 0 && z < n && st[x][y][z]) {
cnt++;
st[x][y][z] = 0;
q.push({x, y, z});
}
}
}
return cnt;
}
int main() {
scanf("%d%d%d%d", &m, &n, &l, &t);
for (int k = 0; k < l; k++)
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
scanf("%d", &st[k][i][j]);
int res = 0;
for (int k = 0; k < l; k++)
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (st[k][i][j]) {
int num = bfs(k, i, j);
if (num >= t) res += num;
}
printf("%d\n", res);
return 0;
}
1148. Werewolf - Simple Version
笔记
-
用两重循环枚举所有狼人的可能情况,针对每种情况去验证两个条件
- 有且只有一个狼人说谎
- 一共只有两人说谎
-
由于存在多种情况,题目说明要找最小序列解(实际上也暗示了需要枚举),因此当循环找到首个满足的情况时立即返回
#include <iostream>
using namespace std;
const int N = 102;
int n, a[N];
int judge(int k, int i, int j) {
// 已知编号为i和j的是狼人,验证编号为k的人说的是真话还是谎话
// 如果编号为k的人说的是谎话,返回1,否则返回0
int x = a[k];
if (x > 0) {
// 编号为k的人说x是好人
if (x == i || x == j) return 1; // 说狼人为好人,在说谎
else return 0; // 说好人是好人,没说谎
} else {
x = -x;
// 编号为k的人说x是狼人
if (x == i || x == j) return 0; // 说狼人为狼人,没说谎
else return 1; // 说好人是狼人,在说谎
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++) {
int s = judge(i, i, j) + judge(j, i, j);
if (s != 1) continue; // 不满足有且只有一个狼人说谎的条件
s = 0;
for (int k = 1; k <= n; k++)
s += judge(k, i, j);
if (s == 2) {
// 恰有两人说谎
cout << i << ' ' << j << endl;
return 0;
}
}
puts("No Solution");
return 0;
}
1051. Pop Sequence
笔记
- 题意:已知入栈顺序、栈大小以及一个弹出序列,判断弹出序列是否合法
-
用栈模拟弹出序列
- 用一个指针遍历弹出序列
-
每次往栈压入一个元素
- 检查栈内元素个数是否超过m个。如果超过,则不合法。
- 如果栈不为空,检查栈顶元素是否与指针指向的元素相等
- 如果相等则出栈,并让指针移到下一个元素,重复直至栈空或不相等
-
如果结束后,栈为空,说明是合法弹出序列,否则不是
#include <iostream>
#include <stack>
using namespace std;
const int N = 1010;
int m, n, k, a[N];
bool judge(int a[], int m) {
stack<int> s;
for (int i = 1, j = 0; i <= n; i++) {
s.push(i);
if (s.size() > m) return false;
while(s.size() && s.top() == a[j]) {
j++;
s.pop();
}
}
return s.empty();
}
int main() {
scanf("%d%d%d", &m, &n, &k);
for (int i = 0; i < k; i++) {
for (int j = 0; j < n; j++)
scanf("%d", &a[j]);
if (judge(a, m)) puts("YES");
else puts("NO");
}
return 0;
}
1055. The World’s Richest
笔记
- 按年龄给所有数据分类,同一年龄内再按净资产降序排列
-
可用
struct Person存储一个富翁的信息,然后重定义<,让两个Person类型的变量a和b能用a < b表示题目所要求的排序次序- 第一关键字:薪金(非升序)
- 第二关键字:年龄(非降序)
- 第三关键字:名字(非降序)
-
输出指定个数的富翁时,可用桶排序,其中桶按年龄划分。可借助一个数组
int idx[]表示各个桶的桶顶元素索引。当从第i个桶取出元素时,让idx[i]++。当idx[i] >= persons[i].size()时,表示第i个桶已经全部取出,即桶空。 - 由于年龄个数不超过200,因此每次查询计算次数不超过200 \times 100 = 2 \times 10^4。查询次数至多为10^3,因此时间复杂度不超过2 \times 10^7 < 5 \times 10^7,能让C++在0.5s内完成。因此可直接顺序查找所有桶顶的最小元素,而不用实现复杂的堆排序优化时间复杂度
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10, M = 210;
struct Person {
string name;
int age;
int w;
bool operator< (const Person& a) const {
if (w != a.w) return w > a.w;
else if (age != a.age) return age < a.age;
else return name < a.name;
}
};
vector<Person> persons[M]; // 按年龄划分富翁(桶)
int idx[M]; // 各个桶的桶顶索引
int n, k;
int main() {
scanf("%d%d", &n, &k);
char name[10];
int w, age;
while(n--) {
scanf("%s%d%d", name, &age, &w);
persons[age].push_back({name, age, w});
}
for (auto& elem : persons) sort(elem.begin(), elem.end());
int m, age_min, age_max;
for (int i = 1; i <= k; i++) {
scanf("%d%d%d", &m, &age_min, &age_max);
printf("Case #%d:\n", i);
memset(idx, 0, sizeof idx); // 重置桶顶指针
bool exist = false;
while(m--) {
int t = -1; // 当前富翁排名最高所在的桶索引
for (int age = age_min; age <= age_max; age++){
if (idx[age] >= persons[age].size())
continue; // 桶为空
if (t == -1 || persons[age][idx[age]] < persons[t][idx[t]]) {
t = age;
}
}
if (t == -1) break; // 没有在范围内的富翁了
Person& p = persons[t][idx[t]];
idx[t]++;
exist = true;
printf("%s %d %d\n", p.name.c_str(), p.age, p.w);
}
if (!exist) puts("None");
}
return 0;
}
1057. Stack
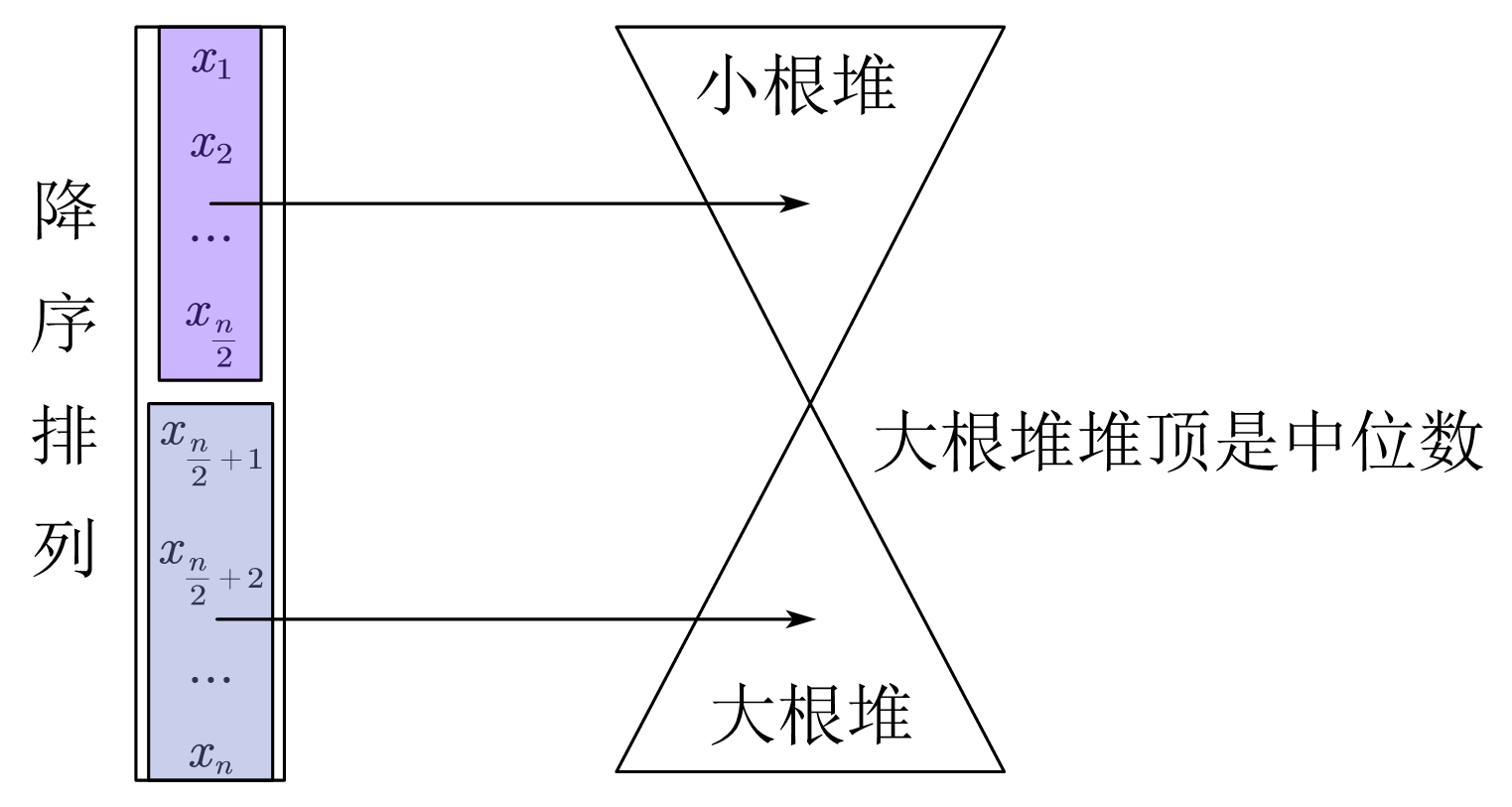
笔记
-
为了实现快速查询中位数的功能,可额外使用“对顶堆”这个数据结构:
- 它包含一个小根堆和一个大根堆,其中小根堆保存最大的一半个元素,大根堆保存最小的一半个元素,保证大根堆的元素至多比小根堆多一个
- 大根堆的堆顶就是当前所有元素的中位数
-
由于本题具有删除操作,而且STL中的堆不支持任意删除的操作,因此采用集合
set实现这个数据结构。由于本题可能包含重复元素,因此需要用多重集合multiset,它位于头文件set中。 - 多重集合
multiset的使用方法:multiset.begin()和it = multiset.end(); it--分别返回多重集合的最小值和最大值在其迭代器的位置,而*multiset.begin()和*it才是表示多重集合的最小值和最大值。- 删除某个元素通过
multiset.erase(multiset.find(x))实现。不用multiset.erase(x)的原因是,这个操作会删除集合里所有重复的x,而前者只会删除其中一个重复元素。
-
STL中的集合类型是基于平衡二叉树实现的,能通过迭代器快速访问最大最小值,且删除操作的时间复杂度为
O(log(n)),因此能代替STL中的堆实现“对顶堆”。假设小根堆为up,大根堆为down,则小根堆up的堆顶位于up.begin(),大根堆down的堆顶位于it = down.end(); it--,中位数就是*it。因此对顶堆有如下操作-
插入元素
- 当小根堆为空或当前元素小于小根堆的堆顶时,将元素插入到大根堆,否则插入到小根堆。
- 插入完毕后需要调整大根堆和小根堆的元素个数差值,保证大根堆的元素至多比小根堆多一个。
-
调整对顶堆
- 当小根堆元素个数大于大根堆时,将小根堆的堆顶插入到大根堆中,并删除小根堆堆顶,重复此过程直至小根堆元素个数不大于大根堆。由于要删除的元素位于多重集合
begin()处,因此可用up.erase(up.begin())实现小根堆的删除操作。 - 当大根堆元素个数大于小根堆的元素个数+1时,将大根堆的堆顶插入到小根堆中,并删除大根堆的堆顶,重复此过程直至大根堆元素个数不大于小根堆的元素个数+1。由于要删除的元素位于多重集合
end()的上一个元素处,不能直接用down.erase(down.end())实现大根堆的删除操作,而应当先获取t = end(),然后用t--获取堆顶位置,在进行插入和删除操作。
- 当小根堆元素个数大于大根堆时,将小根堆的堆顶插入到大根堆中,并删除小根堆堆顶,重复此过程直至小根堆元素个数不大于大根堆。由于要删除的元素位于多重集合
-
删除元素:
- 取出中位数元素,如果当前元素大于中位数元素,则在小根堆删除该元素,否则在大根堆删除该元素
- 调整对顶堆
-
#include <iostream>
#include <cstring>
#include <stack>
#include <set>
using namespace std;
struct OppositeHeap {
// 对顶堆
multiset<int> up; // 小根堆(上堆)
multiset<int> down; // 大根堆(下堆)
// 查询中位数
int median() {
if (down.empty())
return -1; // 堆为空
auto it = down.end();
it--;
int median = *it;
return median;
}
// 维护对顶堆元素个数关系
void adjust() {
while(up.size() > down.size()) {
down.insert(*up.begin());
up.erase(up.begin());
}
while(down.size() - up.size() > 1) {
auto it = down.end();
it--;
up.insert(*it);
down.erase(it);
}
}
// 插入元素
void insert(int x) {
if (up.empty() || x < *up.begin()) down.insert(x);
else up.insert(x);
adjust();
}
// 删除元素
void rem(int x) {
if (down.empty()) return;
else {
int mid = median();
if (x <= mid) down.erase(down.find(x));
else up.erase(up.find(x));
}
adjust();
}
};
struct MyStack {
stack<int> s;
OppositeHeap h;
void push(int x) {
s.push(x);
h.insert(x);
}
int pop() {
if (s.empty())
return -1;
int x = s.top();
s.pop();
h.rem(x);
return x;
}
int median() {
return h.median();
}
int size() {
return s.size();
}
bool empty() {
return s.empty();
}
};
int main() {
int n;
cin >> n;
MyStack s;
string op;
int x;
while(n--) {
cin >> op;
if (op == "PeekMedian") {
if (s.empty()) puts("Invalid");
else cout << s.median() << endl;
} else if (op == "Pop") {
if (s.empty()) puts("Invalid");
else cout << s.pop() << endl;
} else {
cin >> x;
s.push(x);
}
}
return 0;
}
1117. Eddington Number
笔记
- 枚举法:首先让数组升序排序,然后从n枚举到1(因为大的满足,小的一定也满足,所以优先找大的)。不妨用
i表示当前假设的爱丁顿数。如果a[n - i] > i,则说明存在爱丁顿数i。 - 当
i == n时a[0] > n成立,由于a[0]是最小里程数,它> n则说明所有里程数都大于n,则爱丁顿数是n - 当
i > 1 && i < n时,若a[n - i] > i成立,则说明a[n - i]至a[n - 1]都大于i,共有(n - 1) - (n -i) + 1=i个,即至少存在i个数大于i,由于是从大到小寻找,因此也知i + 1不是爱丁顿数,故i是最大的爱丁顿数 - 当
i == 1时a[n - 1] > 1成立,由于a[n - 1]是最大里程数,它> 1则说明至少有一个里程数> 1,则爱丁顿数是1 - 如果都不成立,则爱丁顿数为0
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, a[N];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &a[i]);
sort(a, a + n);
int i;
for (i = n; i; i--)
if (a[n - i] > i)
break;
printf("%d\n", i);
return 0;
}
1044. Shopping in Mars
笔记
- 本题类似“Perfect Sequence”,本质也是最优区间搜索,因此问题转换成如何快速找到最优区间以及如何快速计算区间的和
- 假设区间右端点为
i,左端点为j。让i从1遍历到n,对于每个i,找到一个最优的j,使得当j变成j+1后,不再满足条件。为了快速计算区间的和,可用前缀和优化计算。 - 当
i变成i+1时,不妨把令i + 1记为i_new。为了快速找到i_new对应的最优j_new,需要考虑j是否需要回溯。假设最优的j_new < j,由于j-i是一组解,则j-i_new也满足条件,故j_new-i_new不是最优区间,j_new不是i_new对应的最优左端点,因此j_new >= j,无需回溯,故可用双指针算法将区间搜索的时间复杂度从O(n^2)降为O(n) - 首先用双指针算法找到至少需要花费多少货币, 然后再用一次双指针算法遍历找到区间序号最小的解
#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 2e9;
int n, m, s[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &s[i]);
s[i] += s[i - 1];
}
int res = INF;
for (int i = 1, j = 1; i <= n; i++) {
while(s[i] - s[j] >= m) j++;
if (s[i] - s[j - 1] >= m) res = min(res, s[i] - s[j - 1]);
}
for (int i = 1, j = 1; i <= n; i++) {
while(s[i] - s[j] >= m) j++;
if (s[i] - s[j - 1] == res)
printf("%d-%d\n", j, i);
}
return 0;
}
1040. Longest Symmetric String
笔记
-
用枚举法,但不能按左右端点枚举所有串,因为枚举所有串再判断的时间复杂度为O(n^3),从而TLE。可换个角度,枚举中心点。假设当前中心点在
i处:- 对于字符个数为奇数的串,可让指针
l = i - 1和r = i + 1向外展开,找到最大的奇数回文串 - 对于字符个数为偶数的串,可让指针
l = i和r = i + 1向外展开,找到最大的偶数回文串
- 对于字符个数为奇数的串,可让指针
-
因此,首先遍历所有中心点的位置,然后对于每个中心点位置
i,分别按奇数串和偶数串展开,找到最大的回文串,这样时间复杂度变为O(n^2),实际上这是第一类双指针算法。
#include <iostream>
#include <cstring>
using namespace std;
int main() {
string s;
getline(cin, s);
int res = 0, n = s.size();
for (int mid = 0; mid < n; mid++) {
// odd
int l = mid - 1, r = mid + 1;
while(l >= 0 && r < n && s[l] == s[r]) {
l--;
r++;
}
res = max(res, (r - 1) - (l + 1) + 1);
// even
l = mid, r = mid + 1;
while(l >= 0 && r < n && s[l] == s[r]) {
l--;
r++;
}
res = max(res, (r - 1) - (l + 1) + 1);
}
cout << res << endl;
return 0;
}

