第12章 贪心

1037. Magic Coupon

笔记

题意：让两个数组的元素配对，使得各对元素乘积之和最大

思路：

由于$0$乘任何数都为$0$，因此不考虑$0$，因此可能的如下：

• ① 正数×正数=正数
• ② 负数×负数=正数
• ③ 正数×负数=负数

因此只需要考虑①和②，故可把数组分成正负两段，让正数段与正数段配对，负数段与负数段配对。由于两个输出长度不一定相等，且正数段的长度也不一定相等，因此把较长的正数段裁减，删去较小的部分，使得两个正数段长度相等。由于负数×负数=正数，故可去掉负号，转换成正数的情况。

配对策略为贪心：大的配大的，小的配小的。证明可依据排序不等式：

设$a_1 \leqslant a_2 \leqslant \cdots \leqslant a_n$，$b_1 \leqslant b_2 \leqslant \cdots \leqslant b_n$，则有
$$ \sum_{k=1}^n{a_{n-k+1}b_k}\leqslant \cdots \leqslant \sum_{k=1}^n{a_kb_k} $$
因此根据贪心策略获得的结果为最大值。

算法设计思路：

• 排序，让负数段位于左边，正数段位于右边
• 用两个指针分别从两个数组最左边遍历负数段，计算乘积并累计，直至有指针指向非负数时停止
• 用两个指针分别从两个数组最左边遍历负数段，计算乘积并累计，直至有指针指向非正数时停止
• 二者的和即为结果，时间复杂度瓶颈在排序，为$O(n\log n)$

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, m, a[N], b[N];

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    scanf("%d", &m);
    for (int i = 0; i < m; i++) scanf("%d", &b[i]);

    sort(a, a + n);
    sort(b, b + m);

    int res = 0;
    // 负数段
    for (int i = 0; i < n && i < m; i++)
        if (a[i] < 0 && b[i] < 0)
            res += a[i] * b[i];
        else
            break;

    // 正数段
    for (int i = n - 1, j = m - 1; i >= 0 && j >= 0; i--, j--)
        if (a[i] > 0 && b[j] > 0)
            res += a[i] * b[j];
        else
            break;

    printf("%d\n", res);

    return 0;
}

1038. Recover the Smallest Number

笔记

假设$S$是所有数字构成的串的集合，$\prec$是$S$上的字典序关系，显然是全序关系$\preccurlyeq $，即$\forall a,b \in S$，都有$a \preccurlyeq b$或$b \preccurlyeq a$成立，即任意两个数字串都可比。

假设$a_1,a_2,\cdots,a_n$按照全序集$\preccurlyeq$排序后得到$b_1,b_2,\cdots,b_n$，则$b_1b_2\cdots b_n$一定是字典序最小的串（贪心）。

证明：假设$b_1b_2\cdots b_n$是字典序最小的串，且存在$i, j$ 满足$i<j$且$b_j \prec b_i$。若交换$b_i$和$b_j$，则可得到字典序更小的数字串，矛盾。因此字典序最小的串一定是按照全序集$\preccurlyeq$排序后得到数字串。

为了实现自定义排序，可用匿名函数[](string a, string b){...}。

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e4 + 10;
int n;
string s[N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> s[i];

    sort(s, s + n, [](string a, string b) {
       return a + b < b + a; 
    });

    string res;
    for (int i = 0; i < n; i++)
        res += s[i];

    int k = 0;
    while(k + 1 < res.size() && res[k] == '0') k++;
    res = res.substr(k);

    cout << res << endl;

    return 0;
}

1067. Sort with Swap(0, i)

笔记

• 由于位置和元素都是$0$到$n-1$之间的数，且互异。为了理清其中的关系，可借助图论分析

  • 假设数$u$的位置在$v$，则添加一条$u$指向$v$的有向边
  • 由于每个结点的入度和出度都是1，因此由构造的一定是多个环和自环组成的图

• 自环表示元素位于正确位置上，而环说明其中各个元素还未位于正确的位置上。目标是把图变成$n$个自环

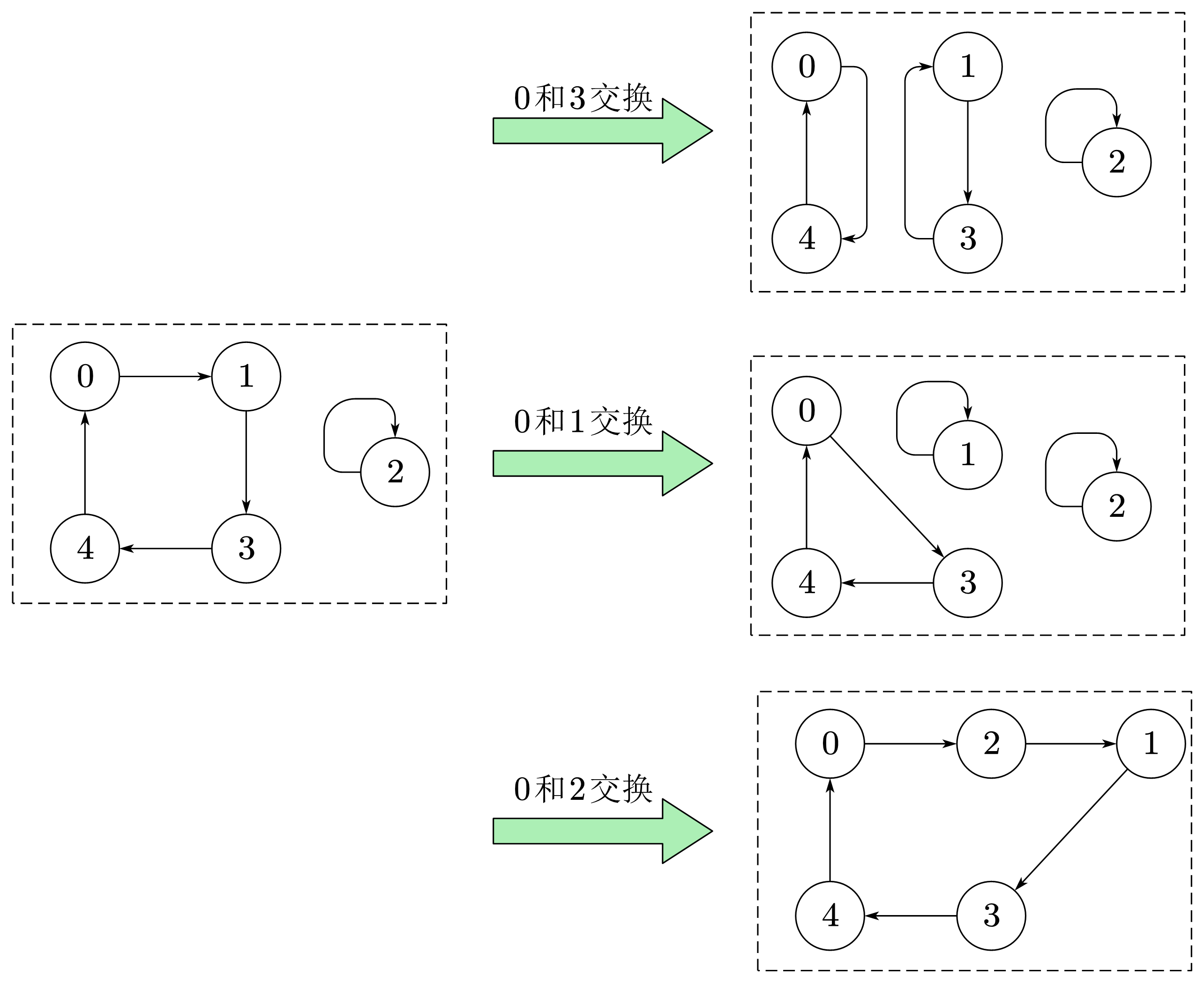
• 假设有五个数$\{4, 0, 2, 1, 3\}$，其图表示如上边所示，由于只能交换$0$和其它元素

  • 与环内的点交换

    • ① 当交换$0$和本环内非邻接结点$3$时，大环被拆成两个小环
    • ② 当交换$0$和本环内邻接结点$1$时，大环被拆成一个小环和一个自环

  • 与环外的点交换

    • ③ 当交换$0$和其它环的结点时，会形成一个大环，即两个环合并

• 操作①拆分环后，之后还得合并，因此含有此操作的一定是多余的。所以最优操作只含有合并操作③和变自环②，而且这些操作的顺序不影响结果。故可考虑先把0所在的环变成自环，然后再去找下一个环。

 #include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n, p[N];

int main () {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &p[i]);

    int res = 0;
    for (int i = 0; i < n; i++) {
        while(p[0]) {
            // 当0不是自环时(即不等于0)，拆掉所在的环
            swap(p[0], p[p[0]]);
            res++;
        }
        while(i < n && p[i] == i) i++;      // 跳过所有自环，寻找大环
        if (i < n) {
            swap(p[0], p[i]);       // 合并到这个环
            res++;
        }
    }

    printf("%d\n", res);

    return 0;
}

1070. Mooncake

笔记

• 类似背包问题，但这里的数量是小数
• 优先选性价比较高的月饼（每千吨价值最高的月饼），证明可用反证法，交换即出现矛盾

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;

struct Cake {
    double num, w;

    bool operator< (const Cake& t) const {
        return w > t.w;
    }
} cake[N];

int main() {
    cin >> n >> m;

    for (int i = 0; i < n; i++)
        cin >> cake[i].num;
    for (int i = 0; i < n; i++) {
        cin >> cake[i].w;
        cake[i].w /= cake[i].num;  // 求单价
    }

    sort(cake, cake + n);

    double res = 0, remain = (double)m;
    for (int i = 0; i < n; i++) {
        double r = min(remain, cake[i].num);
        remain -= r;
        res += r * cake[i].w;
    }

    printf("%.2lf\n", res);

    return 0;
}

1113. Integer Set Partition

笔记

• 排序后，取较小的一半为一个集合，较大的一半为集合

  • 当$n$为奇数时，中位数放到大的集合中，即小集合的下标为0到$\lfloor \frac{n}{2} \rfloor -1$，大集合下标为$\lfloor \frac{n}{2} \rfloor$到$n - 1$
  • 当$n$为偶数时，各取一半，即小集合的下标为0到$\lfloor \frac{n}{2} \rfloor -1$，大集合下标为$\lfloor \frac{n}{2} \rfloor$到$n - 1$

• 综上所述，排序后，让小集合取下标为0到$\lfloor \frac{n}{2} \rfloor -1$的元素，大集合取下标为$\lfloor \frac{n}{2} \rfloor$到$n - 1$的元素

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n, a[N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i ++) scanf("%d", &a[i]);

    sort(a, a + n);

    int s1 = 0, s2 = 0;
    for (int i = 0; i < n / 2; i ++) s1 += a[i];
    for (int i = n / 2; i < n; i ++) s2 += a[i];

    printf("%d %d\n", n % 2, s2 - s1);

    return 0;
}

1125. Chain the Ropes

笔记

• 本题是霍夫曼树的变种，各个绳子的长度可看做赋有点权的叶节点，若叶结点$i$距根节点的路径长度记为$d_i$，点权记为$w_i$，则点权路径之和为$\sum_i{\frac{w_i}{2^{d_i}}}$，本题的目标是$\min \sum_i{\frac{w_i}{2^{d_i}}}$
• 观察目标可发现，叶节点路径长度越长，所在项$\frac{w_i}{2^{d_i}}$越小，为了使目标最小，最短的两条绳子一定要在最底层，可反正证明。

• 同时还可发现，同层交换不影响最优解，因为路径长度不变，因此一定有个最优解可通过合并最短的两个绳子找到，故可把解空间划分成两部分

  • ① 第一步先合并最短的两个绳子（一定存在最优解）
  • ② 第一步不合并最短的两个绳子（可能存在最优解）

• 因此可在子解空间①中搜索最优解，合并最短两个绳子后，问题变成规模为$n-1$的子问题，递归求解即可

• 此外还可发现，假设$x$和$y$是最短的两条绳子的长度，则$\frac{x + y}{2}$依旧比其它$n-2$个绳子的长度短，因为$\frac{x + y}{2} \leqslant \max\{x, y\} \leqslant other$，因此不需要用堆优化，只需排序一次后，按顺序遍历即可
• 贪心与动态规划的区别：二者都划分了集合，但贪心只关注一定有最优解的子集，找到一个即可；而动态规划关注所有集合，力求找到所有最优解。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4 + 10;
int n;
double a[N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];

    sort(a, a + n);

    for (int i = 1; i < n; i++)
        a[0] = (a[0] + a[i]) / 2;

    printf("%d\n", (int)a[0]);

    return 0;
}

1033. To Fill or Not to Fill

笔记

• 如果起点没有加油站，一定无解

• 之后都是以加油站为临时停车点讨论，为方便起见，把终点也看成一个加油站，其油价为$0$。如果汽车停在某个加油站，讨论若汽车在该加油站加满汽油后，在其能行驶最大距离内的加油站情况

  • 如果路上没有加油站，则无解，输出最远距离

  • 若存在一个更比当前加油站价格更便宜的加油站

    • 如果汽车原有汽油足够到达便宜的加油站，则不在当前加油站加汽油，直接过去
    • 如果汽车原有汽油不足够达到便宜的加油站，则在当前加油站加少量汽油，使得刚好能到便宜的汽油站

  • 若路上的加油站都比当前的贵，则先在当地加油站加满汽油，然后再开去路上最便宜的一个加油站加油

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 510;

struct Stop {
    double p, d;

    bool operator< (const Stop& t) const {
        return d < t.d;
    }

} stop[N];

int main() {
    int c_max, dist, d_avg, n;
    cin >> c_max >> dist >> d_avg >> n;
    for (int i = 0; i < n; i++) cin >> stop[i].p >> stop[i].d;
    stop[n] = {0, (double)dist};        // 把终点也当做加油站

    sort(stop, stop + n + 1);

    if (stop[0].d) {
        puts("The maximum travel distance = 0.00");     // 起点无加油站
        return 0;
    }

    double res = 0, oil = 0;
    int i = 0;
    while(i < n) {
        int t = -1;
        for (int j = i + 1; j <= n && stop[j].d - stop[i].d <= c_max * d_avg; j++)
            if (stop[j].p < stop[i].p) {
                // 发现更便宜的加油站
                t = j;
                break;
            } else if (t == -1 || stop[j].p < stop[t].p)
                t = j;      // 在范围里相对便宜

        if (t == -1) {
            // 之后没有加油站支撑继续走
            double max_distance = stop[i].d + (double)c_max * d_avg;
            printf("The maximum travel distance = %.2lf\n", max_distance);     
            return 0;
        }

        if (stop[t].p <= stop[i].p) {
            // 存在更便宜的加油站
            double need = (stop[t].d - stop[i].d) / d_avg;
            if (need > oil) {
                // 剩余的油不够开到这个加油站
                res += (need - oil) * stop[i].p;
                oil = 0;
            } else
                oil -= need;
        } else {
            // 相对便宜
            res += (c_max - oil) * stop[i].p;      // 加满油
            oil = c_max - (stop[t].d - stop[i].d) / d_avg;
        }
        i = t;
    }

    printf("%.2lf\n", res);

    return 0;
}