<---- 我写了这么久，就点个赞吧

$1.$ 树状数组简介

树状数组是一种类似于前缀和的数据结构，但是前缀和的修改操作是 $O(n)$ 的，查询是 $O(1)$ 的 。所以就有了树状数组这个数据结构，它的两种操作被中和了，都是 $O(\log n)$ 的。
线段树也能实现树状数组的功能，但是：相比线段树，树状数组很好写，代码很短！！！

$2.$ 树状数组的基本概念

树状数组是结合了二进制的一种数据结构，它利用二进制来划分每一个节点所表示的前缀和。
这里先给出一张图，这张图很重要，仔细观察就能写出树状数组的代码：

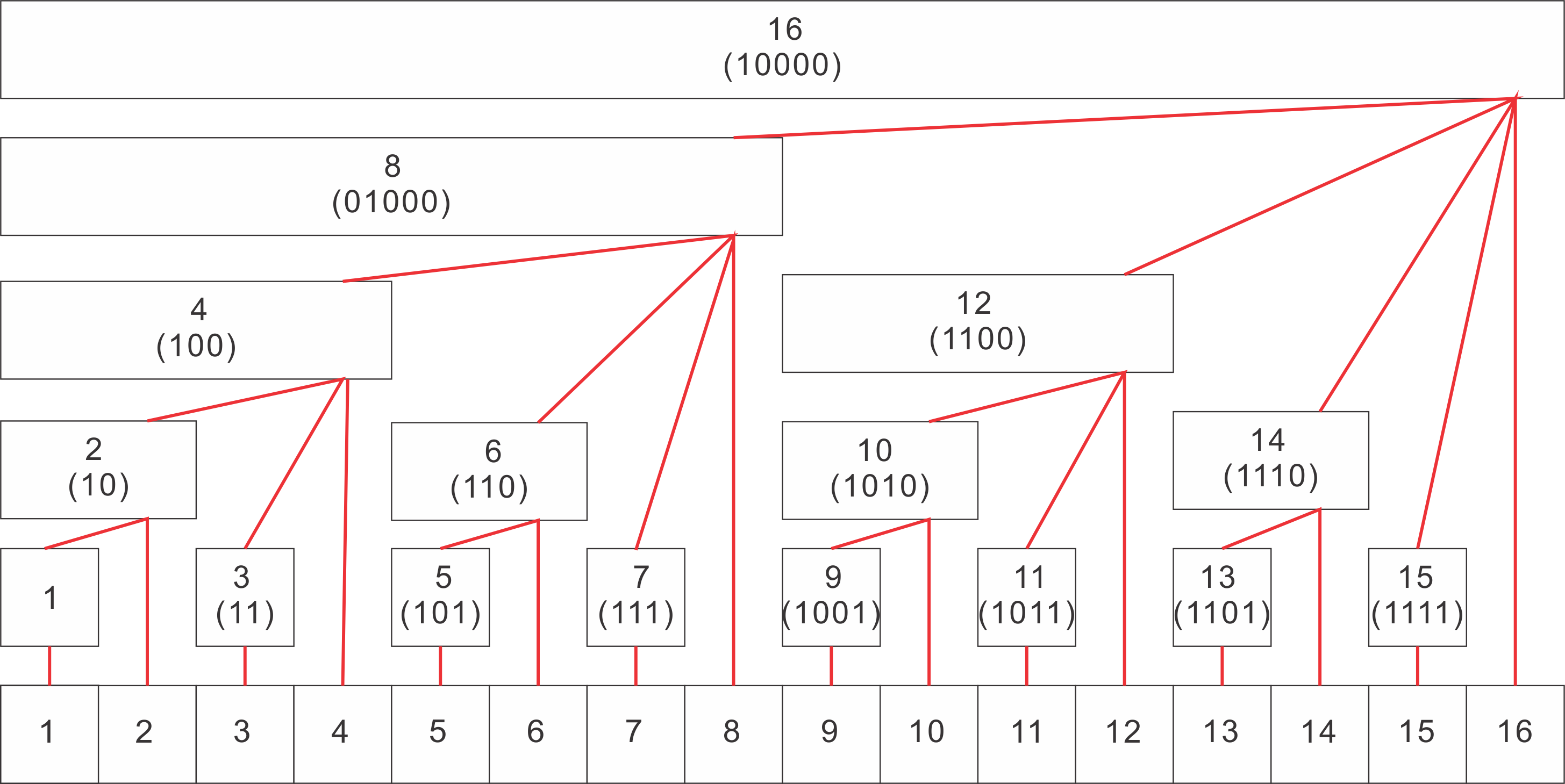
我们能发现一些特点：

• $C_1 = a_1$
• $C_2 = a_1 + a_2$
• $C_3 = a_3$
• $C_4 = a_1 + a_2 + a_3 + a_4$
• $C_5 = a_5$
• $C_6 = a_5 + a_6$
• $C_7 = a_7$
• $C_8 = a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8$

等等
重点来了： $C_i = a_{i - 2^k+1} + a_{i - 2^k+2} + … + a_i$ 其中 $k$ 为 $i$ 的二进制中从最低位到高位连续 $0$ 的长度，即最大的 $k$ 使得 $2^k \le i$
根据 $C_i$ 的公式，我们能够轻松写出求前缀和的公式：$sum_i = C_i+C_{i-k_1}+C_{i-k_1-k_2}+…+C_{i-k_1-k_2}-…-C_{i-k_1-k_2-…-k_t}$ 其中 $k_1,k_2…k_t$ 需满足 $i=2^{k_1}+2^{k_2}+…+2^{k_t}$ 。
由于一个数的具有二进制的唯一分解定理，所以以上的 $k_1,k_2…k_t$ 都是确定的。
这就是树状数组的划分方式。

$3.$ 树状数组的存储方式

直接用数组存储就好了。

$4.$ 建立树状数组

思路

直接开数组就好了

代码

const int N = 100010;
int a[N],c[N];
int lowbit (int x) {    //算出最后一位1的位置，不懂自己查吧
    return x & -x;
}

$5.$ 单点修改

思路

按照上文所说，每次加上去修改的坐标的最后一位 $1$ ，即 $lowbit$ 。
这里是加就是为了为了遍历一条树边，可以对着图片理解
时间复杂度 $O(\log n)$

代码

void add (int x,int d) {
    for (int i = x;i <= n;i += lowbit (i)) c[i] += d;
}

$6.$ 前缀和查询

思路

类似修改，只是不断减去最后一位 $1$ 。
时间复杂度 $O(\log n)$

代码

LL sum (int x) {  //求1~x的和
    LL ans = 0; //开long long，省的爆int
    for (int i = x;i;i -= lowbit (i)) ans += c[i];
    return ans;
}

我写了这么久，你还能不点赞吗