<---- 我写了这么久，就点个赞吧

$1.$ ${Treap}$ 简介

${Treap}$ 是一种平衡树，相比红黑树， ${AVL}$ 要好写一些但代码也很长。

$2.$ ${Treap}$ 的基本概念

${Treap} = {BST}+{Heap}$ ， ${Treap}$ 名字的由来就是 $Tree + Heap$ 。
先来讲一下 ${BST}$ 的一些性质：
1. ${BST}$ 的中序遍历是有序的
2. 只要 ${BST}$ 的中序遍历不变，树的形态无论如何都是不会改变节点之间的关系

第 $2$ 点很重要，这就是 ${Treap}$ 左右旋转的由来！！！
所有平衡树都是用左旋和右旋操作来保持平衡，${Treap}$ 也不例外。
但是大家都知道，如果 ${BST}$ 中，如果插入的顺序是有序的，那么 ${BST}$ 的高度就会达到 $n$ ，导致时间复杂度变高，从 $O(\log n)$ 变成了 $O(n)$ 。
但是如果输入的数据足够随机，那么期望高度就是 $\log n$ 。
所以 ${Treap}$ 就加了一个随机关键字 $val$ ，每次创建一个新节点， $val$ 都会赋值成一个随机数，这个 $val$ 在每一时刻，都应满足堆性质，这里大根堆和小根堆都可以，无所谓，这里就用大根堆了。这就使得 ${Treap}$ 的高度达到 $\log n$ 。

$3.$ 建立 ${Treap}$

思路

${Treap}$ 采用了类似于 $Trie$ 树的存储方法，只不过就是没有第二维，直接把左右儿子的下标存到结构体里了。
为了防止节点越界，一般平衡树都要加两个哨兵 $+∞$ 和 $-∞$
时间复杂度 $O(\log n)$

代码

const int N = 100010,INF = 1e8;
struct Node {   //平衡树节点
    int l,r;    //左右儿子的下标
    int key,val;    //key表示当前点的键值，val表示随机分配的用于更改平衡树形态的的数值
    int cnt,size;   //cnt表示当前值有几个，size表示以当前点为根的子树一共有几个节点
}tr[N]; //平衡树开n个就够了，因为一个点一个数组空间
int root,idx;   //root表示根的下标，就是1，主要是为了方便修改，idx表示当前分配到第几个点，类似于Trie树
int get_node (int key) {    //创建一个节点的键值是key，返回值是当前点在数组中下标
    tr[++idx].key = key;    //直接存入新的节点中
    tr[idx].val = rand ();  //随机分配数值
    tr[idx].cnt = tr[idx].size = 1; //节点数只有当前点
    return idx; //返回当前点在数组中下标
}
void push_up () {   //类似于线段树的push_up，就是上传子树信息
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt;
}
void build_Treap () {   //初始化一个平衡树
    get_node (-INF),get_node (INF); //插入-∞和+∞
    root = 1,tr[root].r = 2;    //这里设-∞为根
    push_up (root);
    if (tr[root].val < tr[tr[root].r].val) left_rotate (root);  //如果不满足堆性质，就旋转，后面会讲
}

$4.$ 旋转

思路

我们要实现一种旋转操作，使得 ${Treap}$ 中的节点关系不变，及中序遍历不变，还要能够交换两个节点的上下位置关系。
我们先给出旋转操作的图片：

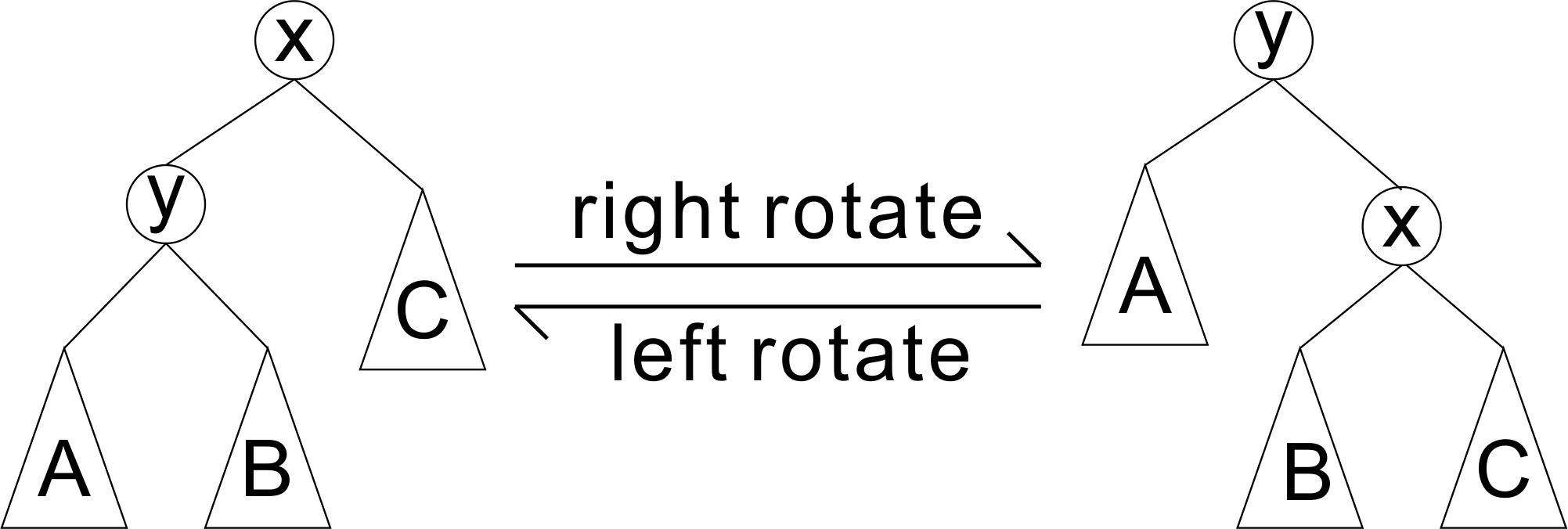
大家是不是发现这些变化的之后的中序遍历不变，这就意味着这样改变是不会影响到键值之间的关系的，所以这样旋转是合法的。对应着上图，我们能够轻松写出代码。
时间复杂度 $O(1)$

代码

void right_rotate (int &p) {    //注意这里是要改变数值的，所以要加引用
    int q = tr[p].l;
    tr[p].l = tr[q].r,tr[q].r = p,p = q;
    push_up (tr[p].r).push_up (p);  //要先push_up子节点，在push_up父节点
}
void left_rotate (int &p) {    //注意这里是要改变数值的，所以要加引用
    int q = tr[p].r;    //可以由right_rotate对应过来，l变成r，r变成l
    tr[p].r = tr[q].l,tr[q].l = p,p = q; 
    push_up (tr[p].l).push_up (p);  //要先push_up子节点，在push_up父节点
}

$5.$ 插入

思路

思路很简单，直接看代码注释吧。
时间复杂度 $O(\log n)$

代码

void insert (int &p,int key) {
    if (!p) p = get_node (key); //这里就体现了引用的作用
    else if (tr[p].key == key) tr[p].cnt++; //如果已经存在这个数了，就cnt++;
    else if (tr[p].key > key) insert (tr[p].l,key); //如果当前点大了，就往左边插入
    else insert (tr[p].r,key);  //否则就从右边插入
    push_up (p);    //记得push_up一下
}

$6.$ 删除

思路

删除操作分为 $3$ 种情况：
1. 如果这个点的数量大于 $1$ 就 $cnt- -$
2. 如果是叶子节点就直接删除
3. 否则就一直使用旋转操作把这个点转到叶子节点上去

直接可以对应到代码上：
时间复杂度 $O(\log n)$

代码

void erase (int &p,int key) {   //同样道理，还是要加引用来修改
    if (!p) return ;    //没有这个点就直接结束
    if (tr[p].key == key) { //找到这个点了
        if (tr[p].cnt > 1) tr[p].cnt--; //当前点的个数大于1就cnt--
        else if (tr[p].l || tr[p].r) {  //当前点不是叶子节点得进行旋转操作旋转到叶子节点上
            if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val) {
            //如果右边是空的或者右转后可以满足堆性质，就直接右旋
                right_rotate (p);
                erase (tr[p].r,key);    //旋转后继续删除
            }
            else {  //否则就左旋
                left_rotate (p);
                erase (tr[p].l,key);
            }
        }
        else p = 0; //是叶子节点就直接删除
    }
    else if (tr[p].key > key) erase (tr[p].l,key);  //如果当前点大了就往左删除
    else erase (tr[p].r,key);   //否则从右边删除
    push_up (p);    //记得要push_up一下
}

$7.$ 给定数值找排名

思路

我们判断给定的数值在哪里，如果没有这个数，返回任意的 $ERROR$ 值；如果这个数在当前点，就要加上左子树的元素个数（想想为什么）；如果在右子树，就要加上当前点的数量和左子树的点数。
对应到代码如下。
时间复杂度 $O(\log n)$

代码

int get_rank_by_key (int p,int key) {
    if (!p) return 0;   //没有这个点就返回排名0
    if (tr[p].key == key) return tr[tr[p].l].size + 1;  //返回最小排名
    if (tr[p].key > key) return get_rank_by_key (tr[p].l,key);  //左边不用变
    return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key (tr[p].r,key);    
    //右边要加上当前点的数量和左子树的数量
}

$8.$ 给定排名找数值

思路

类似于给定数值找排名，直接上代码吧。
时间复杂度 $O(\log n)$

代码

int get_key_by_rank (int p,int rank) {
    if (!p) return INF; //没有当前点，说明排名太大，返回+∞
    if (tr[tr[p].l].size >= rank) return get_key_by_rank (tr[p].l,rank);    //在左边就递归左子树
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key; //在当前点就直接返回
    return get_key_by_rank (tr[p].r,rank - tr[tr[p].l].size - tr[p].cnt);   
    //在右边要剪掉当前点的数量和左子树的点数
}

$9.$ 找前驱

思路

我们先讲一下生么是前驱：

前驱定义为小于 x 的最大的数

这里就直接给出代码，我们用简洁的递归代码来写。
时间复杂度 $O(\log n)$

代码

int get_prev (int p,int key) {
    if (!p) return -INF;    //没有前驱，就返回-INF
    if (tr[p].key >= key) return get_prev (tr[p].l,key); //如果当前点和右边都不可能是答案，就递归左边
    return max (tr[p].key,get_prev (tr[p].r,key));  //否则从当前点的键值和右子树找出来的前驱取max
}

$10.$ 找后继

思路

直接对应找前驱代码。
时间复杂度 $O(\log n)$

代码

int get_next (int p,int key) {  //直接对应get_prev抄下来
    if (!p) return INF;
    if (tr[p].key <= key) return get_next (tr[p].r,key);
    return min (tr[p].key,get_next (tr[p].l,key));
}

我写了这么久，你还能不点赞吗？