更好的阅读体验

KDTree 概念

头文件

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <sstream>
#include <iomanip>
#include <cmath>
#include <bitset>
#include <assert.h>

using namespace std;
typedef long long ll;
typedef set<int>::iterator ssii;

#define Cmp(a, b) memcmp(a, b, sizeof(b))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define Set(a, v) memset(a, v, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define _forS(i, l, r) for(set<int>::iterator i = (l); i != (r); i++)
#define _rep(i, l, r) for(int i = (l); i <= (r); i++)
#define _for(i, l, r) for(int i = (l); i < (r); i++)
#define _forDown(i, l, r) for(int i = (l); i >= r; i--)
#define debug_(ch, i) printf(#ch"[%d]: %d\n", i, ch[i])
#define debug_m(mp, p) printf(#mp"[%d]: %d\n", p->first, p->second)
#define debugS(str) cout << "dbg: " << str << endl;
#define debugArr(arr, x, y) _for(i, 0, x) { _for(j, 0, y) printf("%c", arr[i][j]); printf("\n"); }
#define _forPlus(i, l, d, r) for(int i = (l); i + d < (r); i++)
#define lowbit(i) (i & (-i))
#define MPR(a, b) make_pair(a, b)

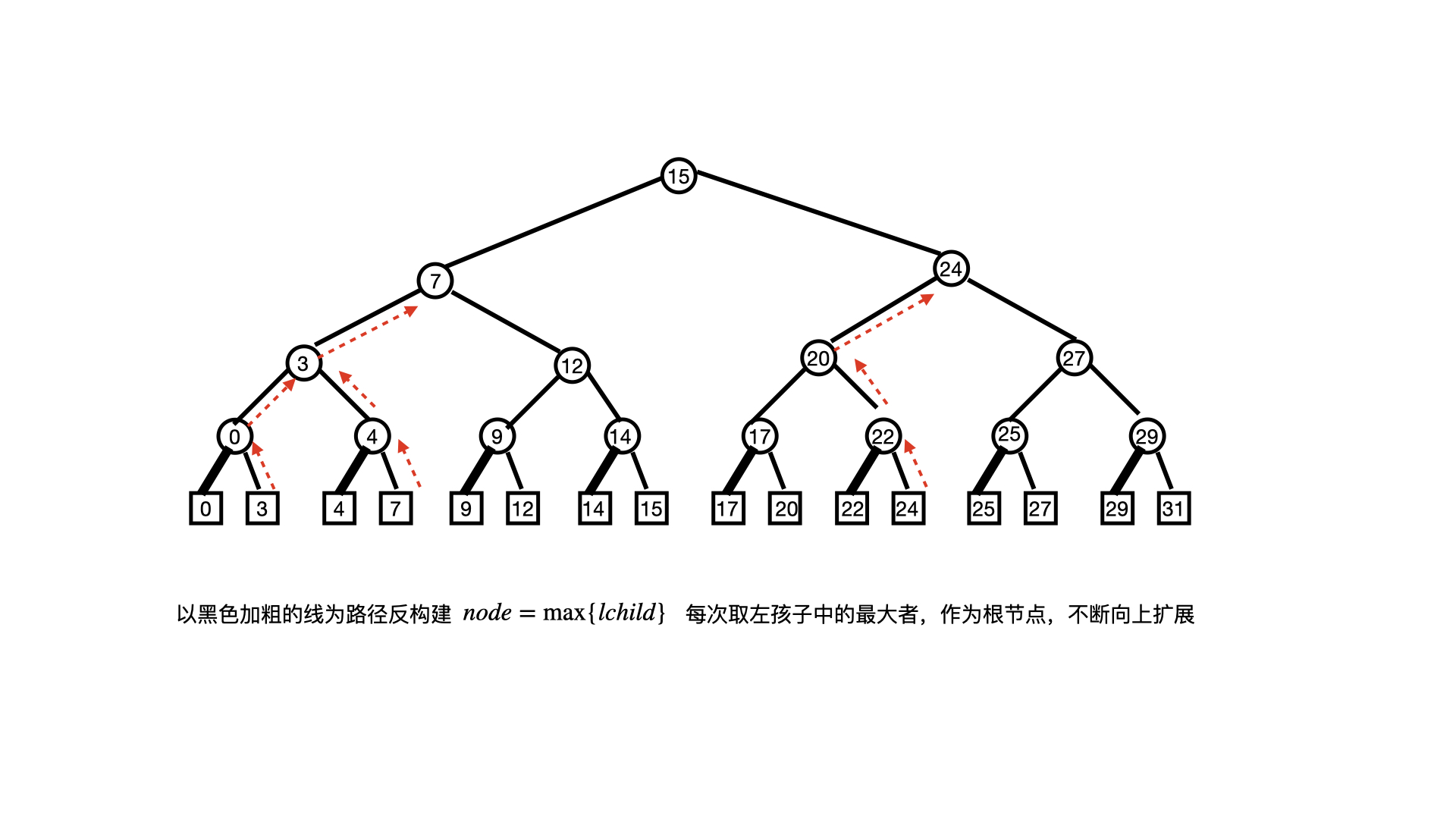
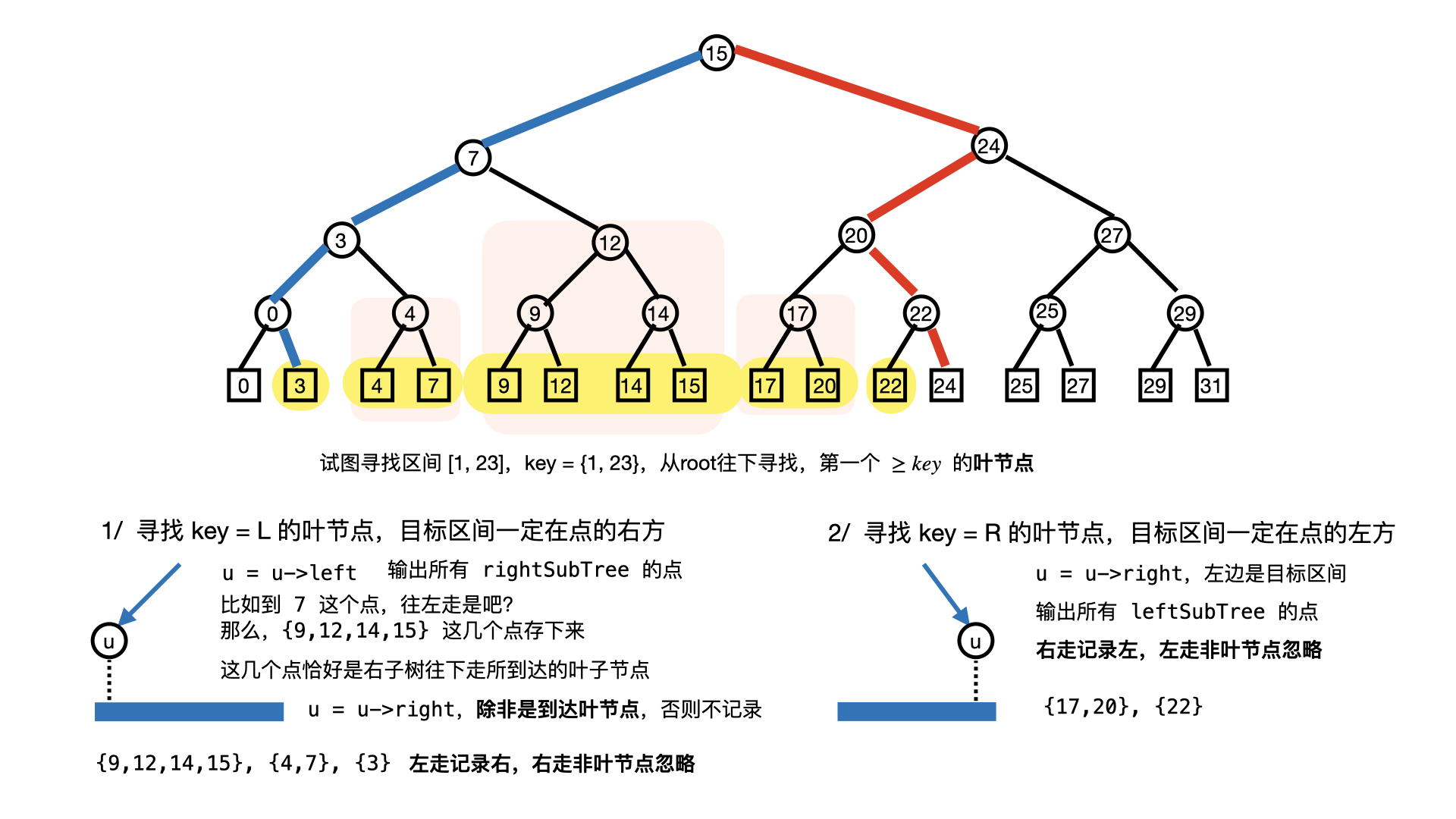
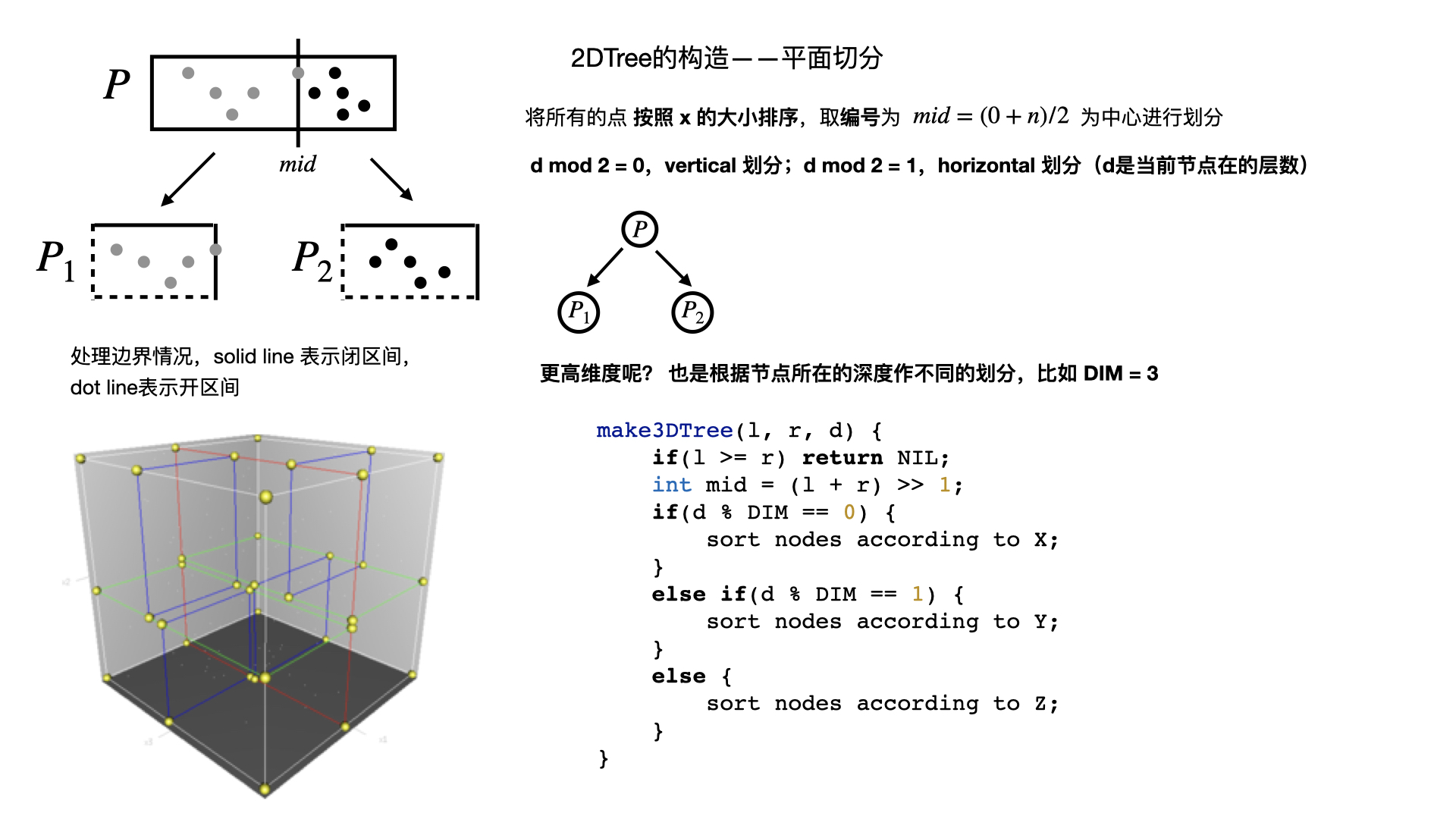
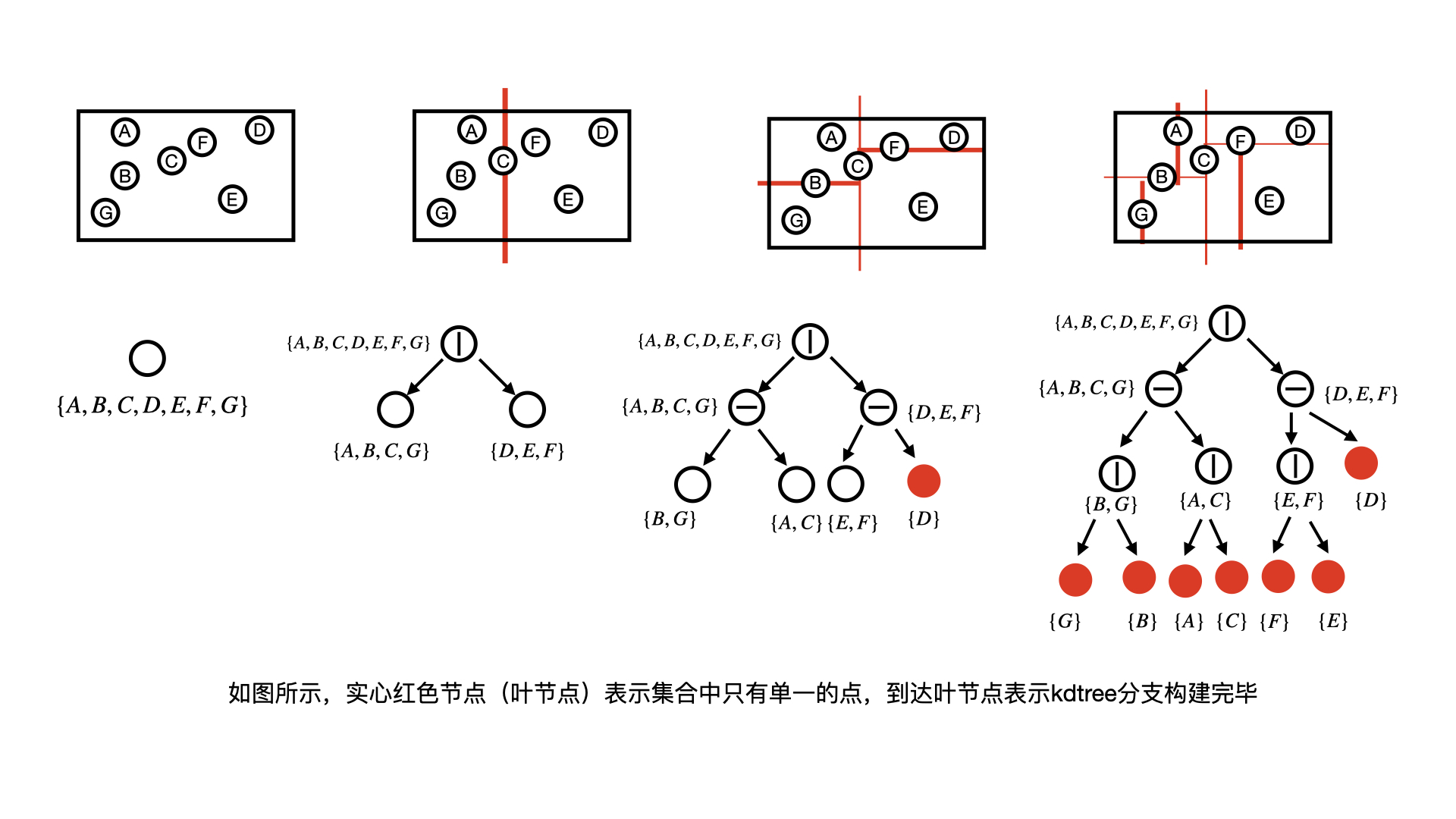
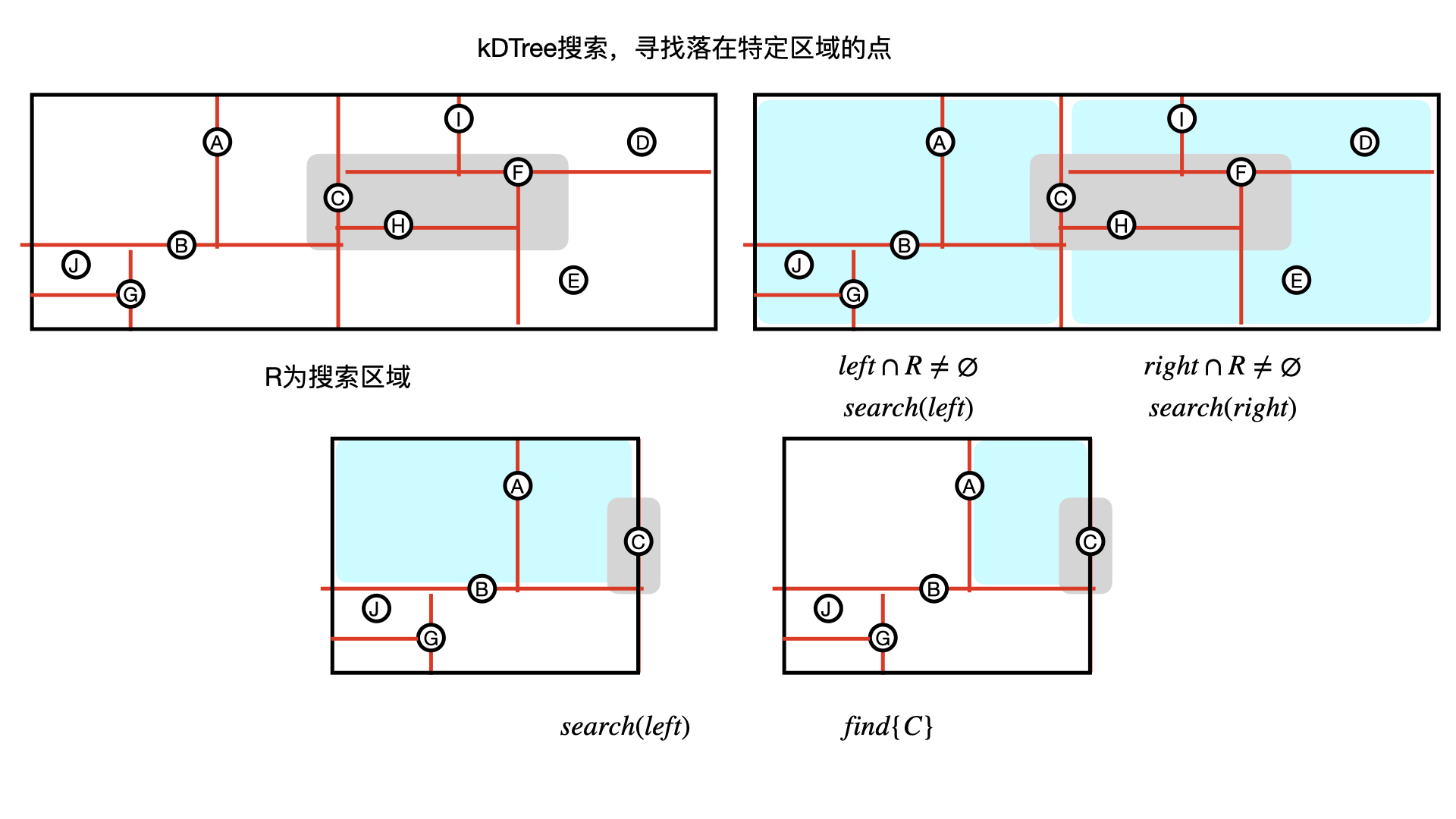
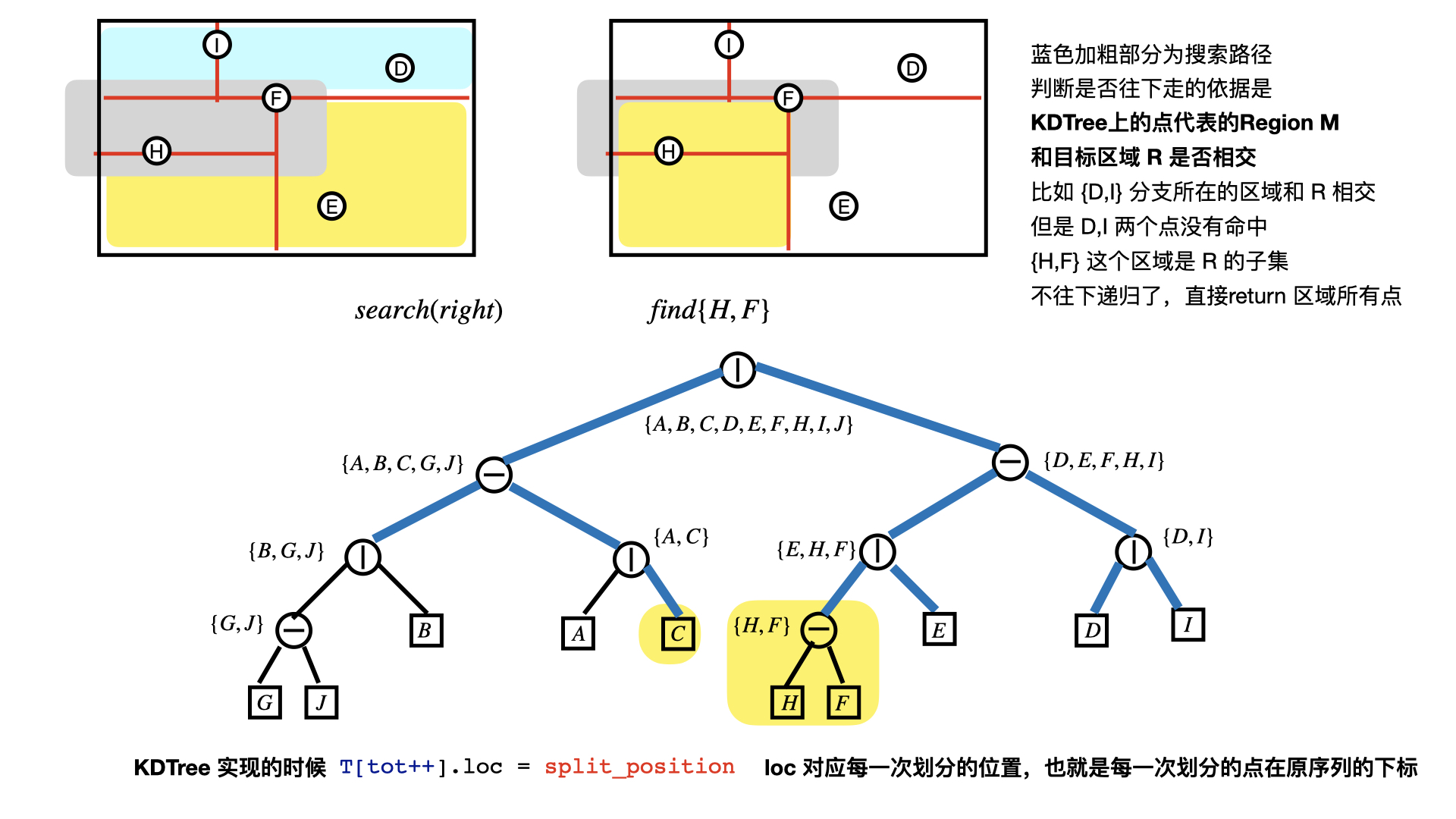
模版

const int maxn = 1e6 + 5;
const int NIL = -1;

// == Point definition ==
class Point {
public:
    int id, x, y;
    Point() {}
    Point(int _id, int _x, int _y) : id(_id), x(_x), y(_y) {}
    bool operator< (const Point& rhs) const {
        return id < rhs.id;
    }

    void print() {
        printf("%d\n", id);
    }
};

Point pt[maxn];

bool cmpx(const Point& p1, const Point& p2) {
    return p1.x < p2.x;
}

bool cmpy(const Point& p1, const Point& p2) {
    return p1.y < p2.y;
}
// == Point finished ==

// == KDTree structure ==
class Node {
public:
    int loc;
    int cld[2];
};

inline int sgn(int d) {
    return d % 2;
}

Node T[maxn];
int tot = 0, root;

void init() {
    tot = 0;
    _for(i, 0, maxn) T[i].cld[0] = T[i].cld[1] = NIL;
}

int buildKD(int l, int r, int d) {
    if(l >= r) return NIL;

    int mid = (l + r) >> 1;

    int t = ++tot;
    if(sgn(d) == 0) sort(pt + l, pt + r, cmpx);
    else sort(pt + l, pt + r, cmpy);

    T[t].loc = mid;
    T[t].cld[0] = buildKD(l, mid, d + 1);
    T[t].cld[1] = buildKD(mid + 1, r, d + 1);

    return t;
}
// == KDTree finished ==

// == query ==
void query(int u, int sx, int tx, int sy, int ty, int d, vector<Point>& ans) {
    int x = pt[T[u].loc].x;
    int y = pt[T[u].loc].y;

    if(sx <= x && x <= tx && sy <= y && y <= ty) ans.push_back(pt[T[u].loc]);

    if(sgn(d) == 0) {
        if(T[u].cld[0] != NIL) {
            if(sx <= x) query(T[u].cld[0], sx, tx, sy, ty, d + 1, ans);
        }
        if(T[u].cld[1] != NIL) {
            if(x <= tx) query(T[u].cld[1], sx, tx, sy, ty, d + 1, ans);
        }
    }
    else {
        if(T[u].cld[0] != NIL) {
            if(sy <= y) query(T[u].cld[0], sx, tx, sy, ty, d + 1, ans);
        }
        if(T[u].cld[1] != NIL) {
            if(y <= ty) query(T[u].cld[1], sx, tx, sy, ty, d + 1, ans);
        }
    }
}
// == query finsihed ==

int N = 0;
int main() {
    freopen("input.txt", "r", stdin);
    int x, y;
    scanf("%d", &N);
    _for(i, 0, N) {
        scanf("%d%d", &x, &y);
        pt[i] = Point(i, x, y);
    }

    init();

    root = buildKD(0, N, 0);

    int q;
    scanf("%d", &q);
    int sx, tx, sy, ty;
    vector<Point> ans;

    _for(i, 0, q) {
        scanf("%d%d%d%d", &sx, &tx, &sy, &ty);
        ans.clear();

        query(root, sx, tx, sy, ty, 0, ans);

        sort(ans.begin(), ans.end());

        _for(k, 0, ans.size()) ans[k].print();
        puts("");
    }
}

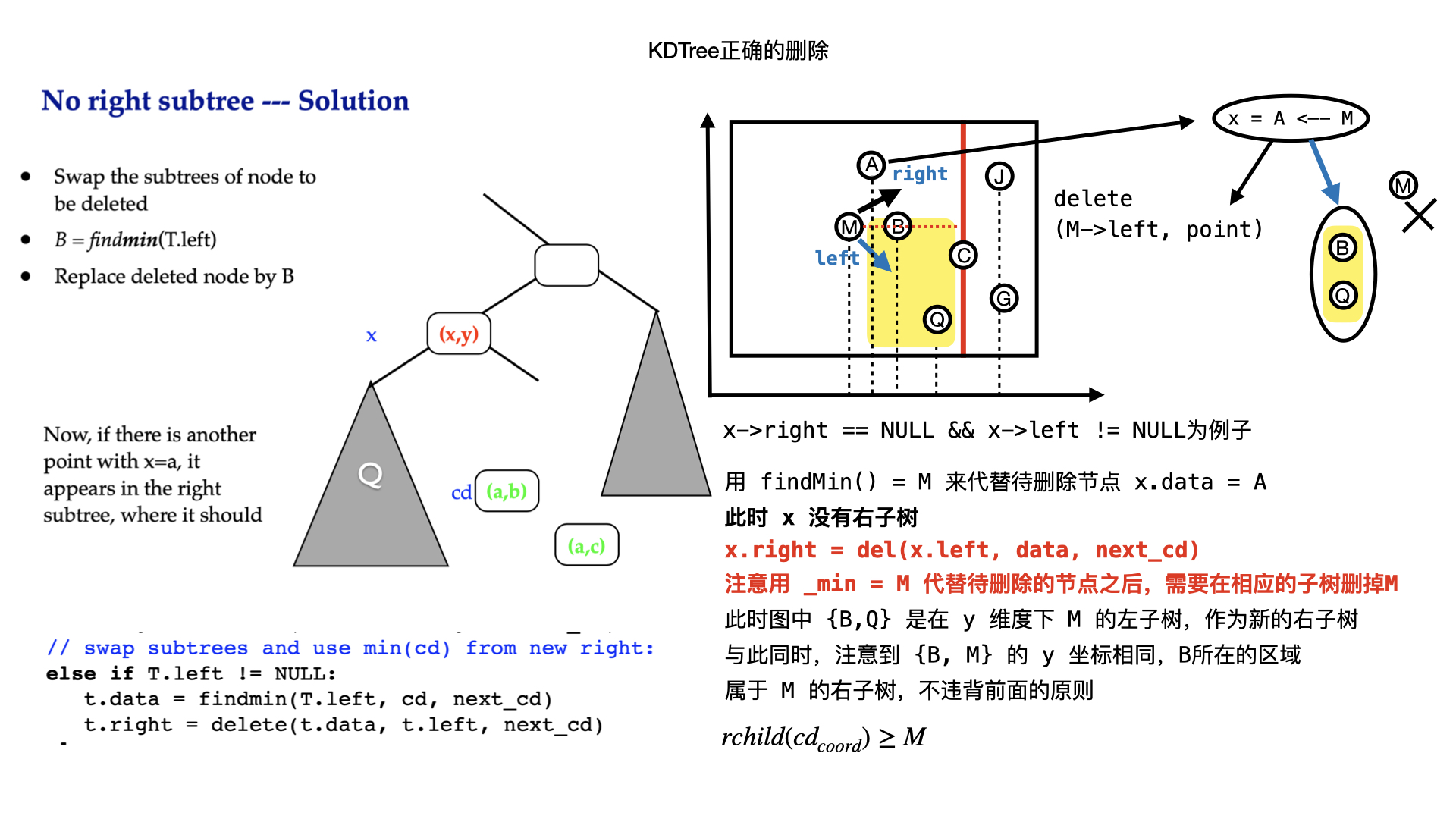
KDTree 插入和删除

注意，kdtree一般的插入或者删除会破坏平衡性
所以一般情况，我们不用插入或者删除
而是采用重新构建kdtree的方法

const int K = 2;
const int inf = 0x3f3f3f3f;

// == tree definition ==
class Node {
public:
    int point[K];
    Node *cld[2];
};

typedef Node* T;

T create(const int arr[]) {
    T cur = new Node();
    _for(i, 0, K) cur->point[i] = arr[i];
    cur->cld[0] = cur->cld[1] = NULL;

    return cur;
}
// == tree finished ==

// == insert function ==
T insertRec(T u, const int point[], int dep) {
    if(u == NULL) return create(point);

    int cd = dep % K;

    if(point[cd] < u->point[cd]) u->cld[0] = insertRec(u->cld[0], point, dep + 1);
    else u->cld[1] = insertRec(u->cld[1], point, dep + 1);

    return u;
}

T insert(T u, const int point[]) {
    return insertRec(u, point, 0);
}
// == insert finished ==

// == search rectangle ==
bool equalPoint(const int point1[], const int point2[]) {
    _for(i, 0, K) if(point1[i] != point2[i]) return false;
    return true;
}

bool searchRec(T u, const int point[], int dep) {
    if(u == NULL) return false;
    if(equalPoint(u->point, point)) return true;

    int cd = dep % K;

    if(point[cd] < u->point[cd]) return searchRec(u->cld[0], point, dep + 1);
    return searchRec(u->cld[1], point, dep + 1);
}

bool search(T u, const int point[]) {
    return searchRec(u, point, 0);
}
// == search finished ==

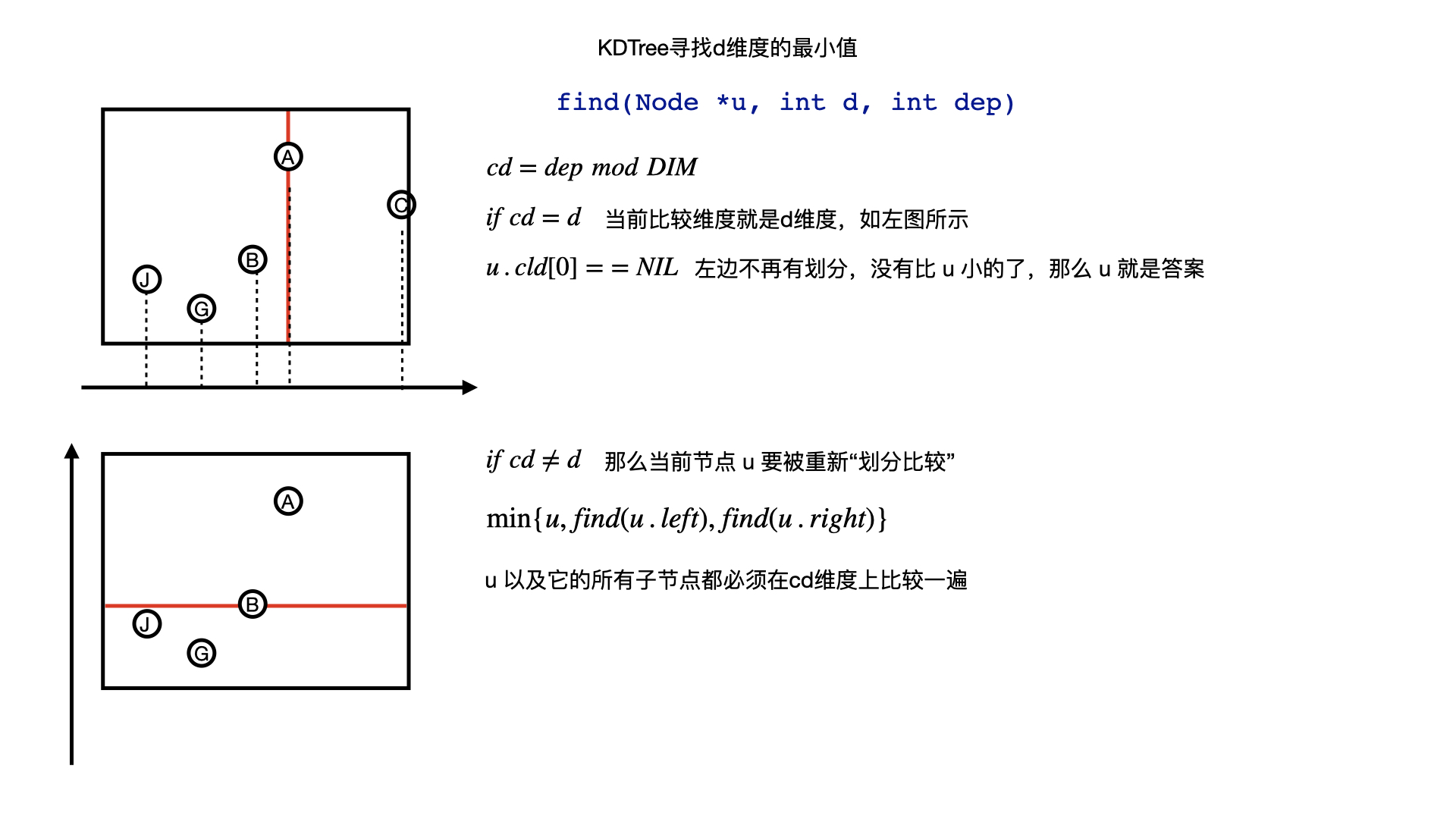
// == find min rec ==
T findMinRec(T u, int _cd, int dep) {
    if(u == NULL) return NULL;

    int cd = dep % K;

    if(cd == _cd) {
        if(u->cld[0] == NULL) return u;
        return findMinRec(u->cld[0], _cd, dep + 1);
    }

    T left = findMinRec(u->cld[0], _cd, dep + 1);
    T right = findMinRec(u->cld[1], _cd, dep + 1);
    T cur = left->point[_cd] < right->point[_cd] ? left : right;

    return cur->point[_cd] < u->point[_cd] ? cur : u;
}

T findMin(T u, int _cd) {
    return findMinRec(u, _cd, 0);
}
// == find finished ==

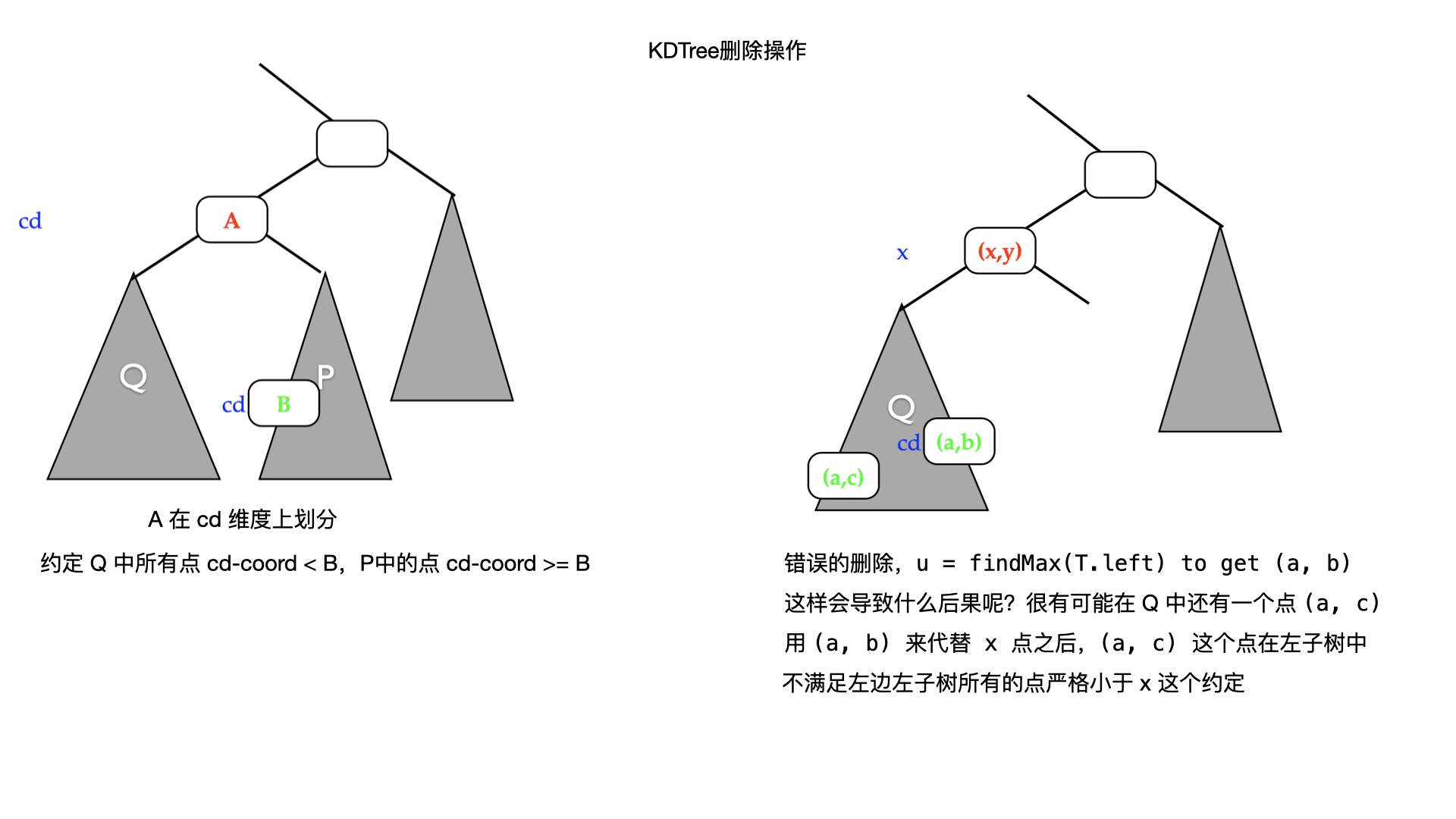
// == delete node ==
void copyPoint(int to[], const int point[]) {
    _for(i, 0, K) to[i] = point[i];
}

T delRec(T u, const int point[], int dep) {
    if(u == NULL) return NULL;

    int cd = dep % K;

    // it is the point to be deleted
    if(equalPoint(u->point, point)) {
        if(u->cld[1]) {
            T _min = findMin(u->cld[1], cd);
            copyPoint(u->point, _min->point);
            u->cld[1] = delRec(u->cld[1], _min->point, dep + 1);
        }

        else if(u->cld[0]) {
            T _min = findMin(u->cld[0], cd);
            copyPoint(u->point, _min->point);
            u->cld[1] = delRec(u->cld[0], _min->point, dep + 1);
        }
        else {
            // is leaf node
            delete u;
            return NULL;
        }
        return u;
    }

    if(point[cd] < u->point[cd]) u->cld[0] = delRec(u->cld[0], point, dep + 1);
    else u->cld[1] = delRec(u->cld[1], point, dep + 1);
    return u;
}

T del(T u, const int point[]) {
    return delRec(u, point, 0);
}
// == delete finished ==

int n;
int main() {
    T root = NULL;
    int points[][K] = {
            {3,6}, {17, 15}, {13, 15}, {6, 12},
            {9, 1}, {2, 7}, {10, 19}
    };

    n = sizeof(points) / sizeof(points[0]);

    _for(i, 0, n) root = insert(root, points[i]);


    int p1[] = {10, 19};
    search(root, p1) ? printf("Found\n") : printf("Not found\n");

    int p2[] = {12, 19};
    search(root, p2) ? printf("Found\n") : printf("Not found\n");

    int p3[] = {10, 19};
    int p4[] = {9, 1};
    del(root, p3);
    search(root, p3) ? printf("Found\n") : printf("Not found\n");
    search(root, p4) ? printf("Found\n") : printf("Not found\n");
}

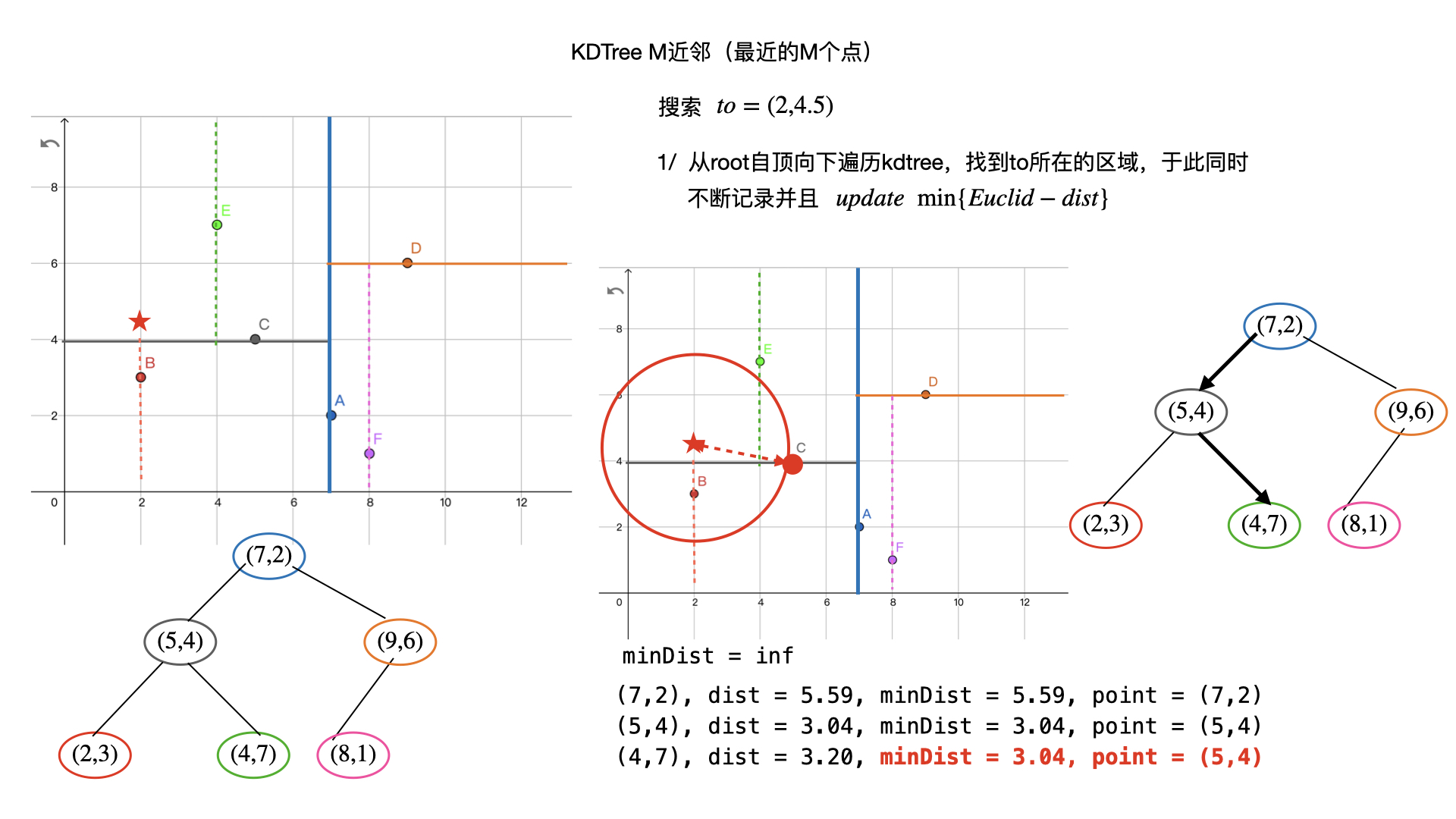
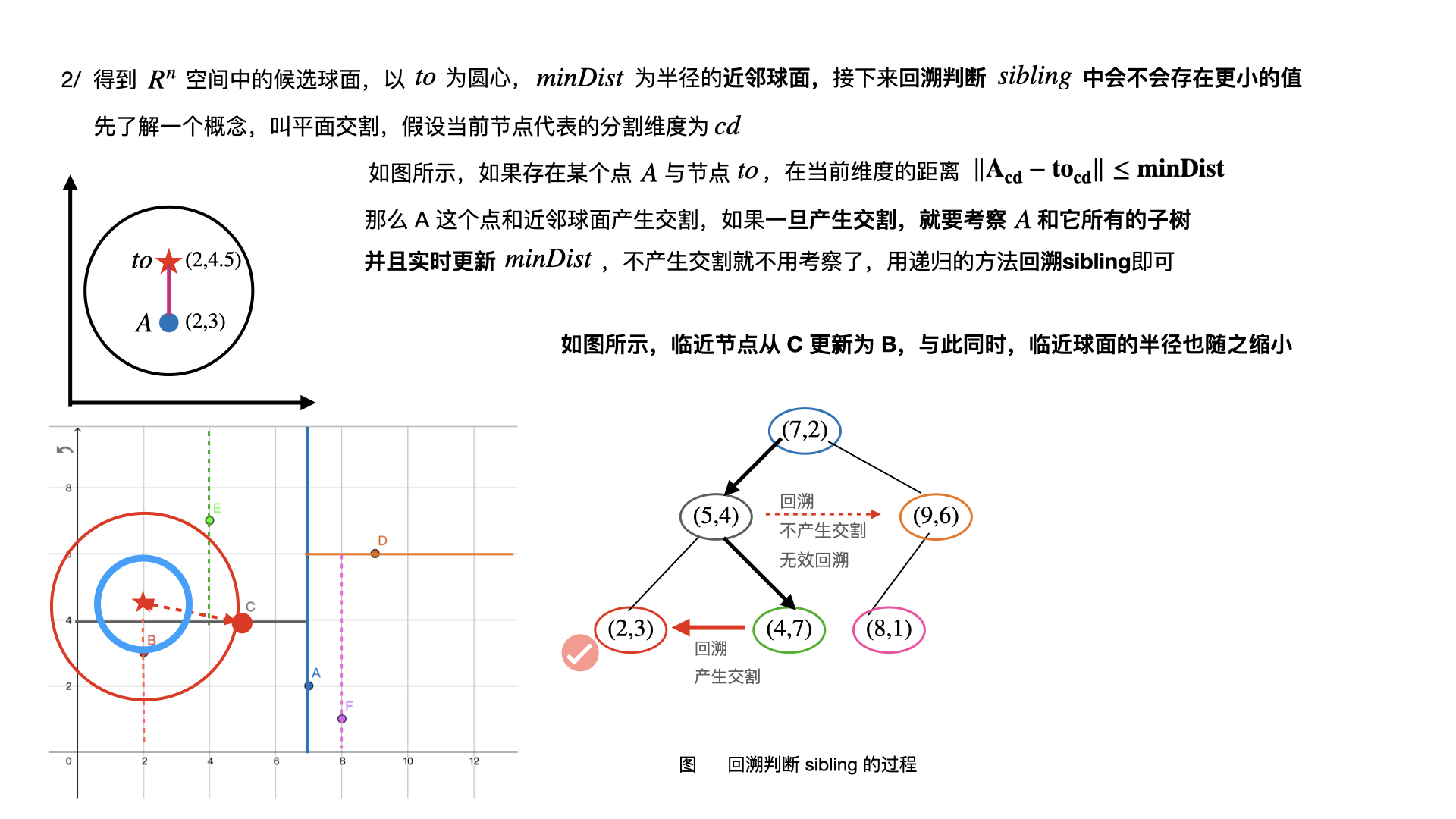
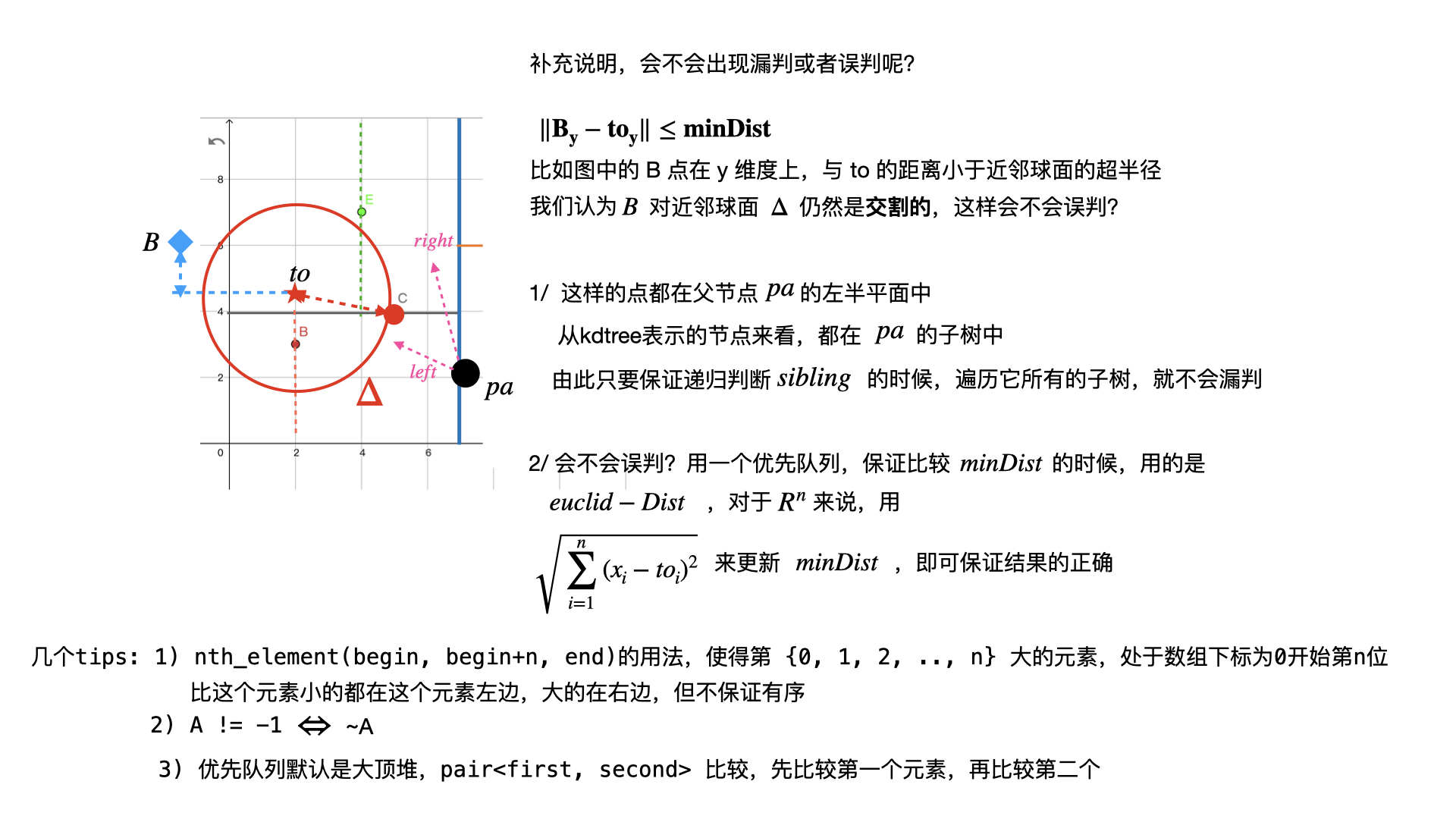
KDTree 找 K 近邻

HDU4347

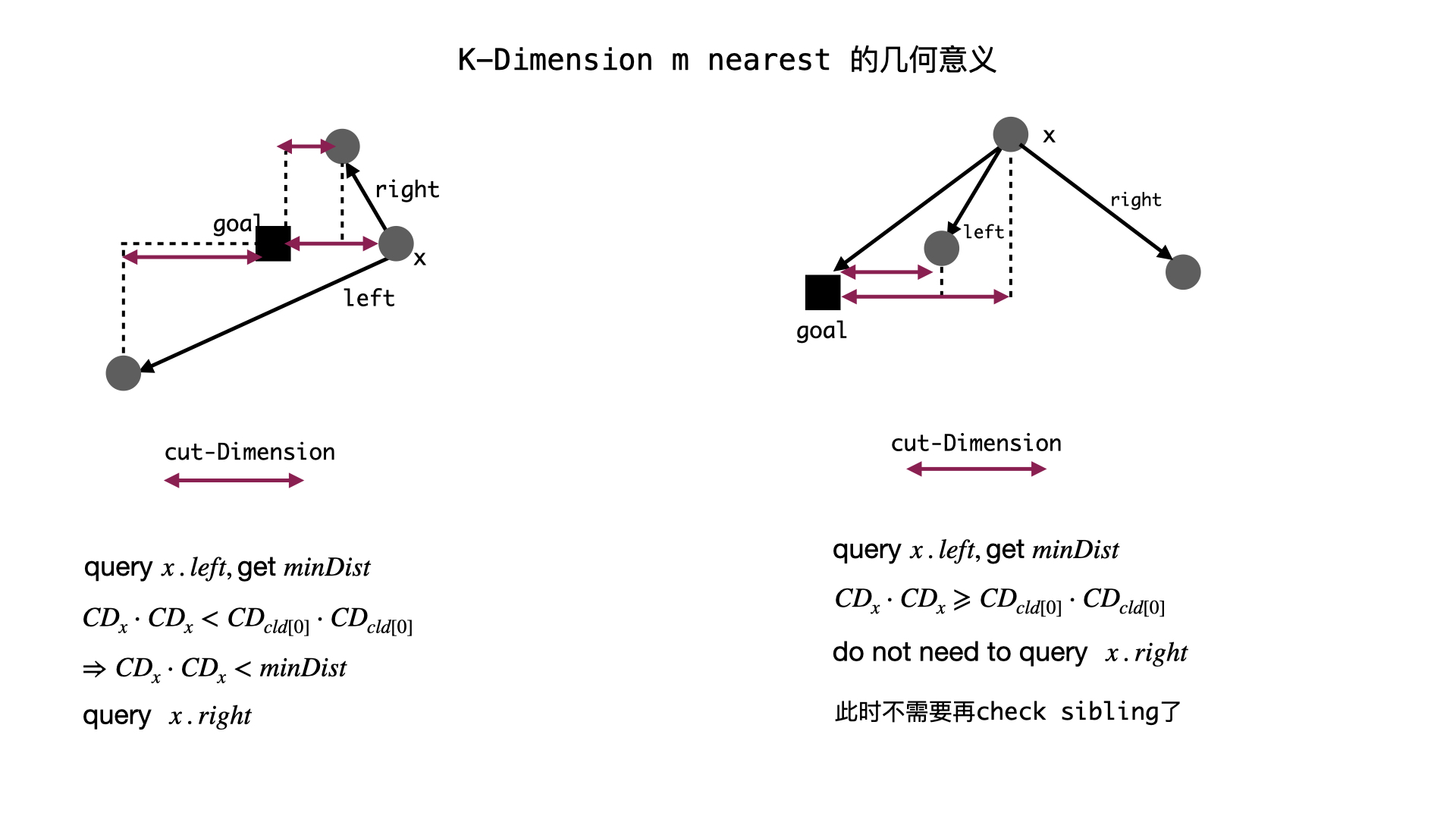
const int maxn = (5e4 + 10) * 2;
const int NIL = 0;
const int inf = 0x3f3f3f3f;

// == KDTree Node definition ==
int cd, K;

class Node {
public:
    int x[6], cld[2];
    ll _max[6], _min[6];

    bool operator< (const Node& rhs) const {
        if(x[cd] != rhs.x[cd]) return x[cd] < rhs.x[cd];
        _rep(i, cd + 1, K) if(x[i] != rhs.x[i]) return x[i] < rhs.x[i];
        _for(i, 1, cd) if(x[i] != rhs.x[i]) return x[i] < rhs.x[i];
        return x[cd] < rhs.x[cd];
    }
};

Node T[maxn];

inline void pushup(int x, int y) {
    _rep(i, 1, K) {
        T[x]._max[i] = max(T[x]._max[i], T[y]._max[i]);
        T[x]._min[i] = min(T[x]._min[i], T[y]._min[i]);
    }
}

int build(int l, int r, int dep) {
    if(l > r) return 0;

    int mid = (l + r) >> 1;
    cd = dep % K;
    nth_element(T + l, T + mid, T + r + 1);
    _rep(i, 1, K) T[mid]._min[i] = T[mid]._max[i] = T[mid].x[i];
    T[mid].cld[0] = T[mid].cld[1] = NIL;

    if(l < mid) {
        T[mid].cld[0] = build(l, mid - 1, dep + 1);
        pushup(mid, T[mid].cld[0]);
    }
    if(r > mid) {
        T[mid].cld[1] = build(mid + 1, r, dep + 1);
        pushup(mid, T[mid].cld[1]);
    }

    return mid;
}

int rt;
// == KDTree finished ==

int n, m, q;

// == temp node for update ==
typedef pair<ll, Node> PLN;
priority_queue<PLN> que;


ll euclid(const Node& a, const Node& b) {
    ll ans = 0;
    _rep(i, 1, K) ans += 1ll * (a.x[i] - b.x[i]) * (a.x[i] - b.x[i]);
    return ans;
}
// == temp node finsihed ==

// == k closest query ==
Node goal;

void query(int u, int dep) {
    if(!u) return;
    ll res = euclid(T[u], goal);

    if(res < que.top().first) {
        que.pop();
        PLN cur(res, T[u]);
        que.push(cur);
    }

    int cd = dep % K;
    ll cut = T[u].x[cd] - goal.x[cd];

    if(cut > 0) {
        query(T[u].cld[0], dep + 1);
        if(cut*cut < que.top().first) query(T[u].cld[1], dep + 1);
    }
    else {
        query(T[u].cld[1], dep + 1);
        if(cut*cut < que.top().first) query(T[u].cld[0], dep + 1);
    }
}
// == k closest query finsiehd ==

void init() {
    _rep(i, 1, K) T[0]._max[i] = -inf, T[0]._min[i] = inf;
}

int main() {
    freopen("input.txt", "r", stdin);
    while (~scanf("%d%d", &n, &K)) {
        init();
        _rep(i, 1, n) _rep(j, 1, K) scanf("%d", &T[i].x[j]);

        // build KDTree and use KDTree
        rt = build(1, n, 1);
        // finished

        scanf("%d", &q);
        while (q--) {
            _rep(i, 1, K) scanf("%d", &goal.x[i]);

            scanf("%d", &m);
            PLN _NIL(inf, Node());
            _rep(i, 1, m) que.push(_NIL);

            // query closest m points
            query(rt, 1);
            stack<PLN> stk;
            while (!que.empty()) {
                stk.push(que.top());
                que.pop();
            }
            printf("the closest %d points are:\n", m);
            while (!stk.empty()) {
                PLN ans = stk.top();
                stk.pop();
                _rep(i, 1, K) {
                    printf("%d", ans.second.x[i]);
                    i != K ? printf(" ") : printf("\n");
                }
            }
        }
    }
}

HDU5992

const int maxn = (200000 + 5) * 2;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int NIL = 0;

// == KDTree definition ==
int cd, K = 2;

class Node {
public:
    int x[2], cld[2];
    int cost, id;

    bool operator< (const Node& rhs) const {
        return x[cd] < rhs.x[cd];
    }
} T[maxn];

int rt;

// usage, build(1, n, 0)
int build(int l, int r, int dep) {
    if(l > r) return 0;

    int mid = (l + r) >> 1;
    cd = dep % K;
    nth_element(T+l, T+mid, T+r+1);
    T[mid].cld[0] = T[mid].cld[1] = NIL;

    if(l < mid) T[mid].cld[0] = build(l, mid - 1, dep + 1);
    if(r > mid) T[mid].cld[1] = build(mid + 1, r, dep + 1);

    return mid;
}
// == KDTree definition finsished ==

// == ans used for update ==
ll euclid(const Node& a, const Node& b) {
    ll ans = 0;
    _for(i, 0, K) ans += 1ll * (a.x[i] - b.x[i]) * (a.x[i] - b.x[i]);
    return ans;
}

bool valid(const Node& cur, const Node& goal) {
    return cur.cost <= goal.cost;
}

typedef pair<ll, Node> PLN;
PLN ans;
// == ans finsihed ==

// == query ==
void query(int u, const Node& goal, int dep) {
    if(!u) return;
    ll res = euclid(T[u], goal);

    if(res == ans.first && T[u].id < ans.second.id && valid(T[u], goal)) {
        PLN cur(res, T[u]);
        ans = cur;
    }

    if(res < ans.first && valid(T[u], goal)) {
        PLN cur(res, T[u]);
        ans = cur;
    }

    int cd = dep % K;
    ll cut = T[u].x[cd] - goal.x[cd];

    if(cut > 0) {
        query(T[u].cld[0], goal, dep + 1);
        if(cut*cut < ans.first) query(T[u].cld[1], goal, dep + 1);
    }
    else {
        query(T[u].cld[1], goal, dep + 1);
        if(cut*cut < ans.first) query(T[u].cld[0], goal, dep + 1);
    }
}
// == query finsihed ==

int n, m;

void init() {
    K = 2;
}

int main() {
    freopen("input.txt", "r", stdin);
    int kase;
    scanf("%d", &kase);

    while (kase--) {
        init();

        // == input data ==
        scanf("%d%d", &n, &m);
        _rep(i, 1, n) {
            _for(j, 0, 2) scanf("%d", &T[i].x[j]);
            scanf("%d", &T[i].cost);
            T[i].id = i;
        }
        // == input finsihed ==

        // == build kdtree ==
        rt = build(1, n, 0);
        // == build finsihed ==

        for(; m; m--) {
            Node goal;
            _for(j, 0, 2) scanf("%d", &goal.x[j]);
            scanf("%d", &goal.cost);

            PLN _NIL(inf, Node());
            ans = _NIL;
            // == query for closest point ==
            query(rt, goal, 0);
            // == query finsihed ==

            _for(i, 0, K) printf("%d ", ans.second.x[i]);
            printf("%d\n", ans.second.cost);
        }
    }
}

KDTree 统计区间点数(莫队)

UVA12939

const int maxn = 200000 + 10;
const int NIL = 0;
int n, d, m;

// == Point definition ==
class Point {
public:
    int x, y;
} PO[maxn];
// == Point finsihed ==

// == Node definition ==
int ID[maxn];
     /* used for mapping ID */

int K = 2, cd;

class KDTree {
public:
    int xy[2], xymin[2], xymax[2];
    int cld[2];
    int sum, fa, num;

    bool operator< (const KDTree& rhs) const {
        return xy[cd] < rhs.xy[cd];
    }
    inline void update();
    inline void _init(int i);
} T[maxn];

inline void KDTree::_init(int i) {
    ID[fa] = i;
    _for(j, 0, K) xymax[j] = xymin[j] = xy[j];
    num = sum = 0;
    cld[0] = cld[1] = NIL;
}

inline void KDTree::update() {
    _for(i, 0, K) if(cld[i]) _for(j, 0, K) {
        xymin[j] = min(xymin[j], T[cld[i]].xymin[j]);
        xymax[j] = max(xymax[j], T[cld[i]].xymax[j]);
    }
}

int build(int l, int r, int dep, int _fa) {
    if(l > r) return NIL;
    int mid = (l + r) >> 1;

    cd = dep % K;
    nth_element(T + l, T + mid, T + r + 1);
    KDTree& cur = T[mid];
    //assert(cur.fa != 0);

    cur._init(mid);
    assert(ID[cur.fa] == mid);
    cur.fa = _fa;

    if(l < mid) cur.cld[0] = build(l, mid - 1, dep + 1, mid);
    if(r > mid) cur.cld[1] = build(mid + 1, r, dep + 1, mid);
    cur.update();

    return mid;
}

int root;
// == Node definition finished ==

// == KDTree query ==
ll ANS[maxn];

inline bool inRange(int x, int l, int r) {
    return l <= x && x <= r;
}
int query(int u, int x1, int x2, int y1, int y2) {
    int res = 0;

    const KDTree& cur = T[u];
    if(cur.xymin[0] > x2 || cur.xymax[0] < x1 || cur.xymin[1] > y2 || cur.xymax[1] < y1 || cur.sum == 0) {
        return 0;
    }
    if(x1 <= cur.xymin[0] && cur.xymax[0] <= x2 && y1 <= cur.xymin[1] && cur.xymax[1] <= y2) {
        return cur.sum;
    }

    if(inRange(cur.xy[0], x1, x2) && inRange(cur.xy[1], y1, y2)) res += cur.num;
    _for(i, 0, K) if(cur.cld[i]) {
        res += query(cur.cld[i], x1, x2, y1, y2);
    }

    return res;
}
// == KDTree query finished ==

// == Mo algo ==
int belong[maxn];
int sz, t;

class Qry {
public:
    int l, r, id;
} qry[maxn];

void block() {
    sz = sqrt(n);
    t = n / sz;
    _rep(i, 1, t) _rep(k, (i - 1) * sz + 1, i * sz) belong[k] = i;
    if(t * sz < n) {
        t++;
        _rep(k, (t - 1) * sz + 1, n) belong[k] = t;
    }
}

bool cmp(const Qry& a, const Qry& b) {
    if(belong[a.l] ^ belong[b.l]) return belong[a.l] < belong[b.l];
    return a.r < b.r;
}

void add(int pos, ll& ans) {
    ans += query(root, PO[pos].x - d, PO[pos].x + d, PO[pos].y - d, PO[pos].y + d);
    int ti = ID[pos];
    T[ti].num = 1;
    while (ti) T[ti].sum++, ti = T[ti].fa;
}

void del(int pos, ll& ans) {
    int ti = ID[pos];
    T[ti].num = 0;
    while (ti) T[ti].sum--, ti = T[ti].fa;
    ans -= query(root, PO[pos].x - d, PO[pos].x + d, PO[pos].y - d, PO[pos].y + d);
}
// == Mo algo finished ==

void init() {
    Set(ID, 0);
    Set(belong, 0);
}

int main() {
    freopen("input.txt", "r", stdin);
    for(int t = 1, x, y; scanf("%d%d%d", &n, &d, &m) == 3; t++) {
        init();
        printf("Case %d:\n", t);

        // input point data
        _rep(i, 1, n) {
            KDTree& cur = T[i];
            scanf("%d%d", &x, &y);
            cur.xy[0] = PO[i].x = x + y;
            cur.xy[1] = PO[i].y = x - y;
            cur.fa = i;
        }

        // build tree
        root = build(1, n, 0, 0);

        // block for Mo algorithm
        // remember sort query then Mo algorithm
        _rep(i, 1, m) {
            scanf("%d%d", &qry[i].l, &qry[i].r);
            qry[i].id = i;
        }
        block();
        sort(qry + 1, qry + 1 + m, cmp);

        // use Mo algo and KDTree query
        int l = 1, r = 0;
        ll ans = 0;
        _rep(i, 1, m) {
            int ql = qry[i].l, qr = qry[i].r;
            while (r < qr) add(++r, ans);
            while (r > qr) del(r--, ans);
            while (l < ql) del(l++, ans);
            while (l > ql) add(--l, ans);

            ANS[qry[i].id] = ans;
        }

        _rep(i, 1, m) printf("%lld\n", ANS[i]);
    }
}

KDTree 和并查集

HDU5809

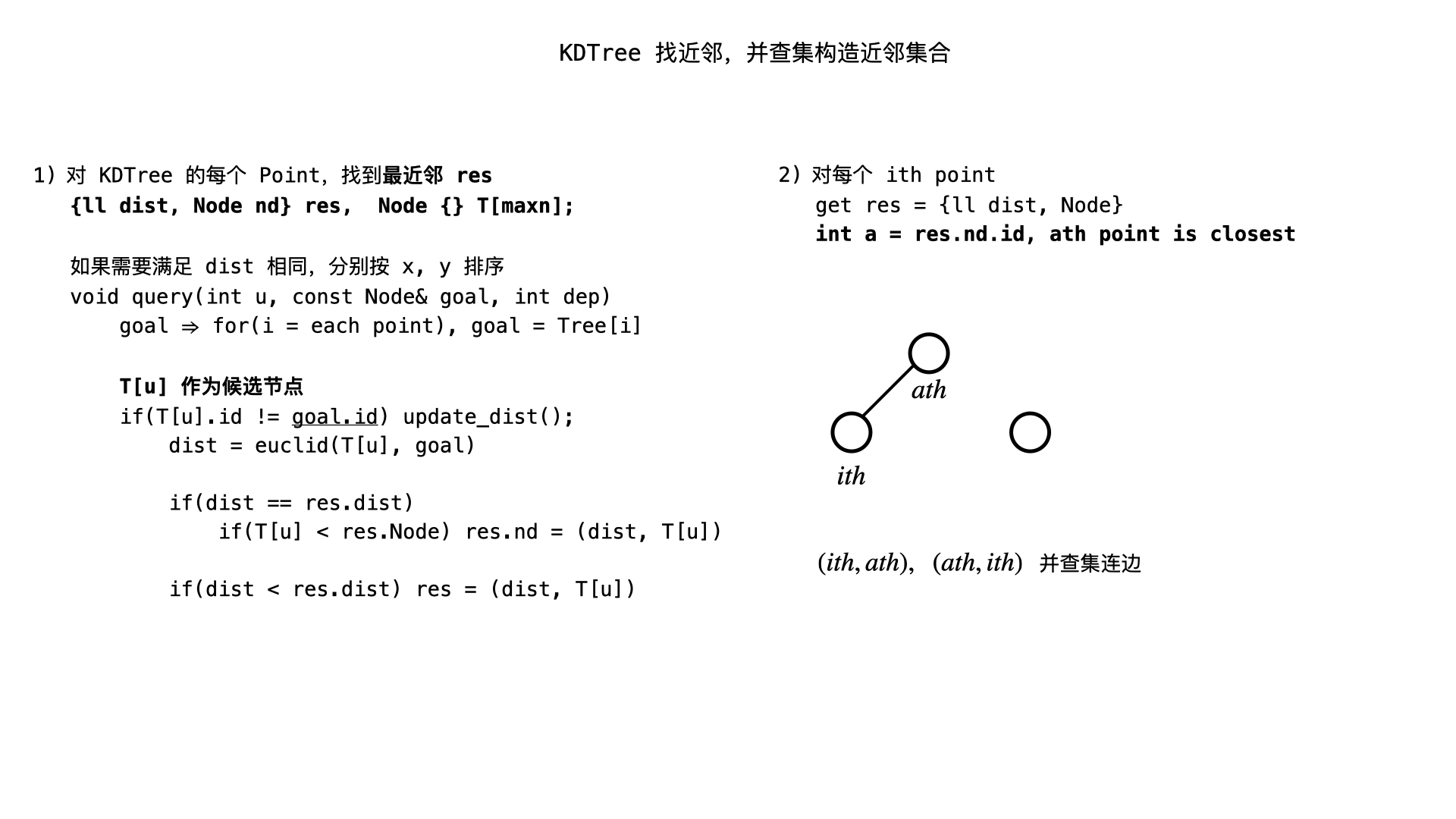
const int maxn = (1e5 + 5) * 2;
const ll inf = 0x3f3f3f3f3f3f3f3f;
const int NIL = 0;
int n, q;
int ID[maxn];

// == KDTree definition ==
int cd, K = 2;

class Node {
public:
    ll x[2];
    int cld[2];
    ll xymax[2], xymin[2];
    int id;

    bool operator< (const Node& rhs) const {
        if(x[0] != rhs.x[0]) return x[0] < rhs.x[0];
        return x[1] < rhs.x[1];
    }

    void _init(int i) {
        ID[id] = i;
        _for(j, 0, K) xymin[j] = xymax[j] = x[j];
        cld[0] = cld[1] = NIL;
    }

    inline void update();

} Tree[maxn];

inline void Node::update() {
    _for(i, 0, K) if(cld[i]) _for(j, 0, K) {
        xymin[j] = min(xymin[j], Tree[cld[i]].xymin[j]);
        xymax[j] = max(xymax[j], Tree[cld[i]].xymax[j]);
    }
}

bool cmp(const Node& a, const Node& b) {
    return a.x[cd] < b.x[cd];
}
// Point cur = pt[Tree[u].id]

int root;
// == KDTree finished ==

// == build tree ==
int build(int l, int r, int dep) {
    if(l > r) return 0;

    int mid = (l + r) >> 1;

    cd = dep % K;
    nth_element(Tree + l, Tree + mid, Tree + r + 1, cmp);

    Tree[mid]._init(mid);
    if(l < mid) Tree[mid].cld[0] = build(l, mid - 1, dep + 1);
    if(mid < r) Tree[mid].cld[1] = build(mid + 1, r, dep + 1);

    Tree[mid].update();
    return mid;
}
// == build fisniehd ==

// == used to solve ==
struct A {
    ll dist;
    Node nd;
    A() {};
    A(ll d, Node nd) : dist(d), nd(nd) {}
} res;
// dist init to inf

inline ll euclid(const Node& a, const Node& b) {
    ll ans = 0;
    _for(i, 0, K) ans += 1ll * (a.x[i] - b.x[i]) * (a.x[i] - b.x[i]);
    return ans;
}

inline ll manhatten(int u, const Node& goal) {
    ll ans = 0;
    const Node& cur = Tree[u];

    _for(i, 0, K) {
        ans += (max(cur.xymin[i] - goal.x[i], 0LL) + max(goal.x[i] - cur.xymax[i], 0LL)) *
                (max(cur.xymin[i] - goal.x[i], 0LL) + max(goal.x[i] - cur.xymax[i], 0LL));
    }

    return ans;
}

void querymin(int u, const Node& goal) {
    if(!u) return;
    if(goal.id != Tree[u].id) {
        ll dist = euclid(goal, Tree[u]);

        if(dist == res.dist && Tree[u] < res.nd) {
            res.nd = Tree[u];
        }

        if(dist < res.dist) {
            res.dist = dist;
            res.nd = Tree[u];
        }
    }

    ll dl = Tree[u].cld[0] ? manhatten(Tree[u].cld[0], goal) : inf;
    ll dr = Tree[u].cld[1] ? manhatten(Tree[u].cld[1], goal) : inf;

    if(dl < dr) {
        if(dl <= res.dist) querymin(Tree[u].cld[0], goal);
        if(dr <= res.dist) querymin(Tree[u].cld[1], goal);
    }
    else {
        if(dr <= res.dist) querymin(Tree[u].cld[1], goal);
        if(dl <= res.dist) querymin(Tree[u].cld[0], goal);
    }
}
// == finsihed ==

// == findset definition ==
int pa[maxn];
int findset(int x) {
    return pa[x] == x ? x : pa[x] = findset(pa[x]);
}
// == findset finsihed ==

// == solve the problem ==
void fi(int i) {
    res = A(inf, Node());
    querymin(root, Tree[ID[i]]);
    int to = res.nd.id;

    int u = findset(i);
    int v = findset(to);

    //printf("#: %d, %d, %d, %d\n", i, to, u, v);
    if(u != v) pa[u] = v;
}
// == solve finished ==

void init() {
    //
    K = 2;
    res = A(inf, Node());
    Set(ID, 0);

    _for(i, 0, maxn) pa[i] = i;
}



int main() {
    freopen("input.txt", "r", stdin);
    int kase;
    scanf("%d", &kase);

    for(int _ = 1; _ <= kase; _++) {
        printf("Case #%d:\n", _);

        init();
        scanf("%d%d", &n, &q);
        _rep(i, 1, n) {
            scanf("%lld%lld", &Tree[i].x[0], &Tree[i].x[1]);
            Tree[i].id = i;
        }

        // build KDTree
        root = build(1, n, 0);
        //_rep(i, 1, n) debug(ID[i]);

        // query min dist
        _rep(i, 1, n) fi(i);

        // debug

        _rep(i, 1, q) {
            int x, y;
            scanf("%d%d", &x, &y);
            findset(x) == findset(y) ? puts("YES") : puts("NO");
        }
    }
}

KDTree 剪枝优化

UVALive7825

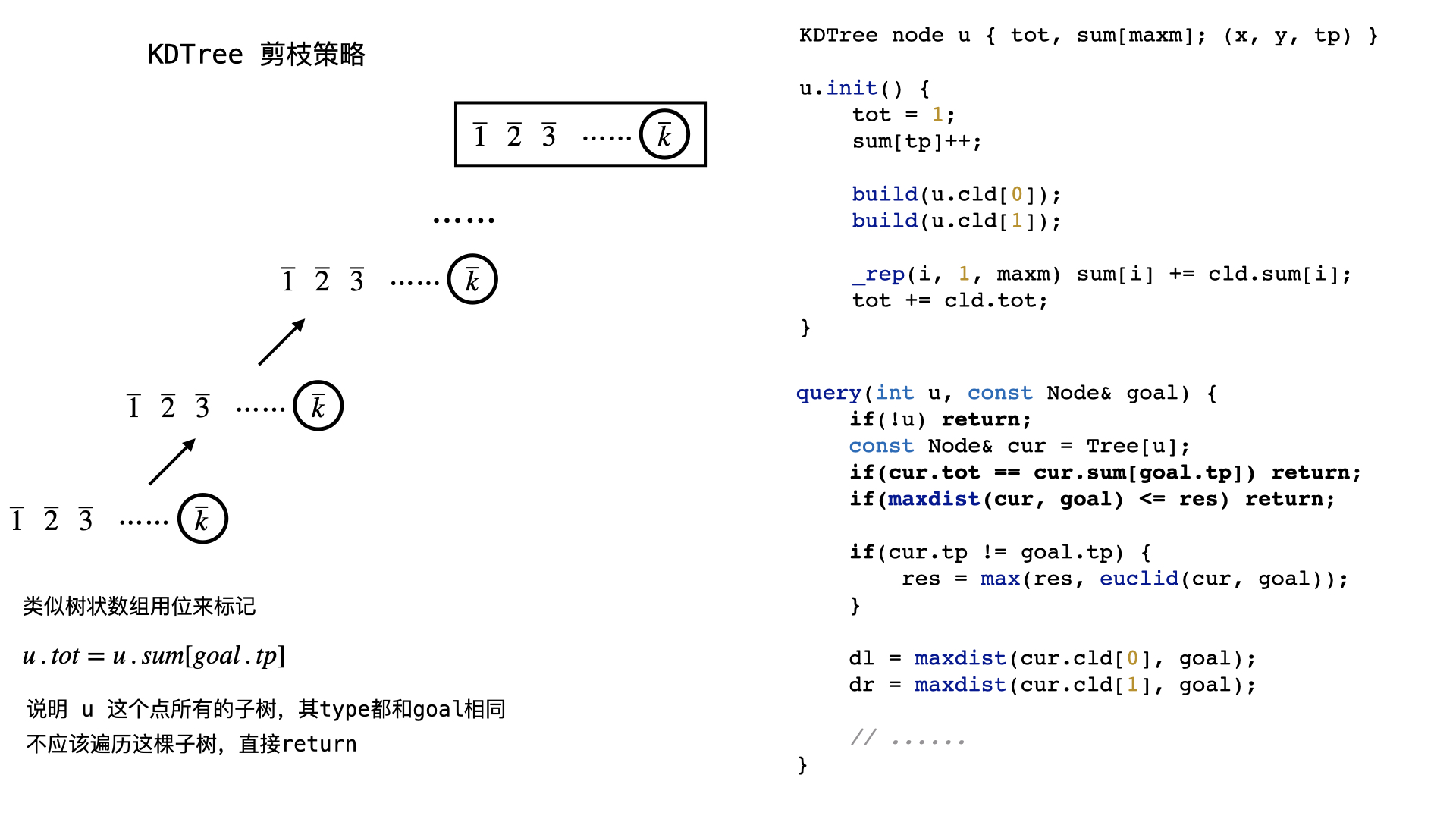
const int inf = 0x3f3f3f3f;
const int maxn = 1e5 + 5;
const int maxm = 100 + 5;
int n;

// == KDTree definition ==
int cd = 0;
const int K = 2;

struct Base {
    int x[2];
    int tp;
} sta[maxn];

class Node {
public:
    Node *cld[2];
    int xy[2];
    int tp;

    int tot;
    int sum[maxm];
    int x1, x2, y1, y2;

    void border(int L, int R, int& _x1, int& _x2, int& _y1, int& _y2) {
        _rep(i, L, R) {
            Base& cur = sta[i];
            _x1 = min(_x1, cur.x[0]);
            _x2 = max(_x2, cur.x[0]);
            _y1 = min(_y1, cur.x[1]);
            _y2 = max(_y2, cur.x[1]);
        }
    }

    inline void _init(int _tp = 0, int _x1 = 0, int _x2 = 0, int _y1 = 0, int _y2 = 0) {
        tot = 0;
        Set(sum, 0);
        cld[0] = cld[1] = NULL;

        x1 = _x1; x2 = _x2; y1 = _y1; y2 = _y2;
        tp = _tp;
    }

    inline void getData(int tid) {
        const Base& _cur = sta[tid];
        _for(i, 0, K) xy[i] = _cur.x[i];
        sum[_cur.tp]++;
        tot = 1;
    }
    void update();
} memory[maxn * 2];

typedef Node* T;
Node *mem = memory;
Node *root;

void Node::update() {
    _for(i, 0, K) if(cld[i]) {
            _for(j, 0, maxm) sum[j] += cld[i]->sum[j];
            tot += cld[i]->tot;
        }
}
// == KDTree finished ==

// == build KDTree ==
inline bool cmp(const Base& a, const Base& b) {
    return a.x[cd] < b.x[cd];
}


void build(T& cur, int l, int r, int dep) {
    if(l > r) return;
    cur = ++mem;

    int _x1, _x2, _y1, _y2;
    _x1 = _y1 = inf;
    _x2 = _y2 = 0;
    cur->border(l, r, _x1, _x2, _y1, _y2);

    //assert(dbg(cur) != 0);
    //debug(dbg(cur));

    cd = dep % K;
    int mid = (l + r) >> 1;
    nth_element(sta + l, sta + mid, sta + r + 1, cmp);

    cur->_init(sta[mid].tp, _x1, _x2, _y1, _y2);
    cur->getData(mid);
    build(cur->cld[0], l, mid - 1, dep + 1);
    build(cur->cld[1], mid + 1, r, dep + 1);

    cur->update();
}

// == build KDTree finished ==

// == used for calculate ==

inline int sqr(int x) {
    return x * x;
}
inline int maxdist(T cur, const Base& goal) {
    if(!cur) return 0;

    int ans = sqr(cur->x1 - goal.x[0]) + sqr(cur->y1 - goal.x[1]);
    ans = max(ans, sqr(cur->x1 - goal.x[0]) + sqr(cur->y2 - goal.x[1]));
    ans = max(ans, sqr(cur->x2 - goal.x[0]) + sqr(cur->y1 - goal.x[1]));
    ans = max(ans, sqr(cur->x2 - goal.x[0]) + sqr(cur->y2 - goal.x[1]));

    return ans;
}

inline int euclid(T cur, const Base& goal) {
    return sqr(cur->xy[0] - goal.x[0]) + sqr(cur->xy[1] - goal.x[1]);
}

void query(const T &cur, const Base& goal, int& res) {
    if(!cur) return;
    if(cur->tot == cur->sum[goal.tp]) return;
    if(maxdist(cur, goal) <= res) return;

    if(cur->tp != goal.tp) {
        res = max(res, euclid(cur, goal));
    }

    int d[2], flag = 1;
    d[0] = maxdist(cur->cld[0], goal);
    d[1] = maxdist(cur->cld[1], goal);

    if(d[0] > d[1]) flag ^= 1;

    if(d[flag] > res) query(cur->cld[flag], goal, res);
    if(d[flag^1] > res) query(cur->cld[flag^1], goal, res);
}

void solve() {
    int ans = 0;
    _rep(i, 1, n) query(root, sta[i], ans);
    printf("%d\n", ans);
}
// == calculate finsihed ==

void init() {
    _for(i, 0, maxn) (memory + i)->_init();
    mem = memory;
    root = NULL;
}

int main() {
    freopen("input.txt", "r", stdin);
    while (scanf("%d", &n) == 1 && n) {
        // input sta data
        _rep(i, 1, n) {
            Base& cur = sta[i];
            scanf("%d%d%d", &cur.x[0], &cur.x[1], &cur.tp);
        }

        init();
        // build KDTree
        build(root, 1, n, 0);
        // solve
        solve();
    }
}