更好的阅读体验
贪心学习笔记(一)

导言

在贪心题目中,排序算法总是和它一起出现,因此我们不难发现,有一类模型名为贪心+排序.

那么接下来,我们通过一道经典题目,感受一下这类模型的贪心为何和排序算法紧密不可分离.

题目描述

神犇航空开展了一项载客特技飞行业务。每次飞行长N个单位时间，每个单位时间可以进行一项特技动作，可选的动作有K种，每种动作有一个刺激程度Ci。如果连续进行相同的动作，乘客会感到厌倦，所以定义某次动作的价值为(距上次该动作的时间)*Ci，若为第一次进行该动作，价值为0。安排一种方案，使得总价值最大。

输入输出格式

输入格式：

第一行，两个数，N和K，如上所述；

第二行，K个正整数，表示K种动作的Ci值。

输出格式：

仅一行，一个整数，表示最大总价值。

输入输出样例

输入样例#1：

5 2
2 2

输出样例#1：

12

说明
对于10%的测试数据，$N \le 20$，$K \le 3$

对于全部的测试数据，$1 \le N \le 1000，1 \le K \le 300，0 \le Ci \le 1000$。

解题报告

题意理解

每一个时刻,你都可以安排一个项目,然后同一个项目,两次安排的时间间隔乘以它的刺激度,就是它的价值.现在请你做出一种安排,使得所有项目价值和最高.

每一个项目,可以安排次数不限.

思路确定

我们首先发现,一个项目其实当且仅当安排两次就好了.

1. 少于两次,那么价值其实为0,还不如不安排.
2. 大于两次,其实价值和两次的价值一样,如下图所示.

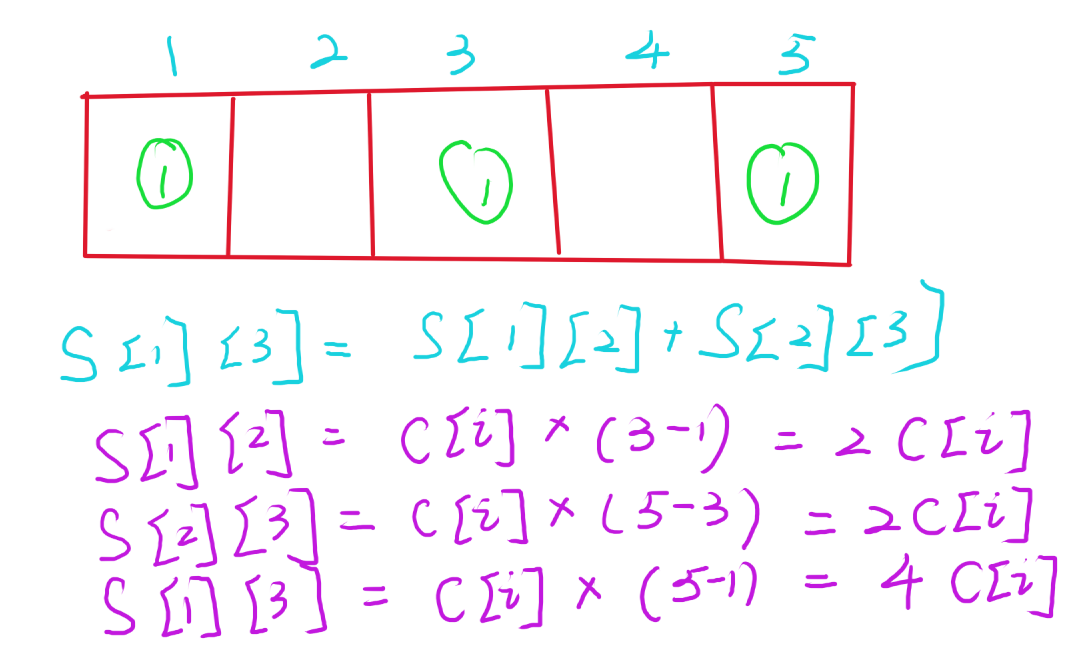
根据上图,我们就可以成功论证,一个项目只会出现两次.

综上所述,我们发现了,对于一个项目而言,间隔的距离最大,那么最后的价值就会最大.

间隔距离最大,那么显然就是最左端放一个,最右端放一个,那么此时显然距离最大.

但是间隔距离,会随着放的项目越来越多,而变得越来越短.

因此为了让最后的权值最大,我们不得不让,价值越高的项目,越在前面放置,使得他们的距离最大.

代码解释

#include <bits/stdc++.h>
using namespace std;
const int N=1100;
int n,m,k,a[N],ans;
int cmp(int a,int b)
{
    return a>b;
}
int main()
{
    cin.tie(0);
    ios::sync_with_stdio(false);
    cin>>n>>k;
    for(int i=1;i<=k;i++)
        cin>>a[i];
    sort(a+1,a+1+k,cmp);//贪心排序.
    m=n-1;//最大距离
    for(int i=1;i<=min(k,n/2);i++)
    {
        ans+=a[i]*m;//加上本次项目的价值
        m-=2;//距离减少两个.因为放入了一对项目.
    }
    cout<<ans;
    return 0;
}