笔记汇总
加工生产调度
首先,按照常规的贪心做法。考虑两个产品 i,j。如果按照 i,j 的顺序,那么有两种情况,我们分别画图解释:
- Aj<=Bi
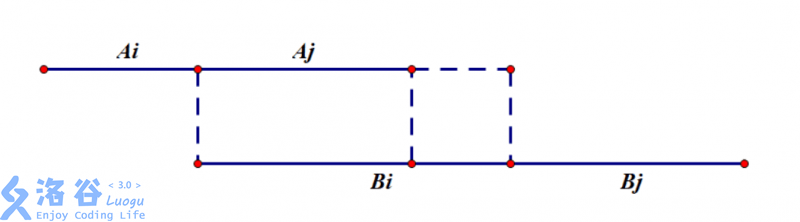
- Aj>Bi
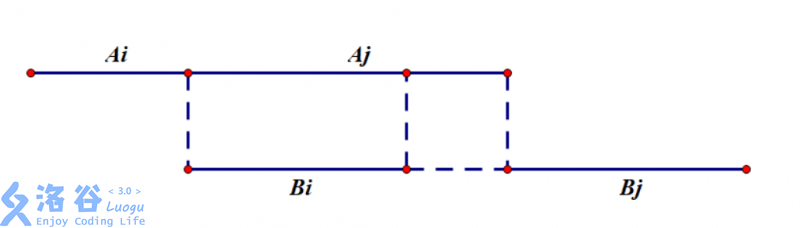
汇总一下,总时间为 Ai+max(Aj,Bi)+Bj=总和−min(Aj,Bi)
用临项交换法可知,min(Ai,Bj)<=min(Aj,Bi) 的关系排序即可,由于 min 是不可比性传递,最好将 B 作为第二关键字,以免出错。
排序完后,A时间短的往前塞,B则往后塞。
然后再去找等到 A 车间加工完: t[i],或等到 B 车间加工完: sum。再取其中最大值。
皇后游戏
容易发现,排序为 min(Ai,Bj)<=min(Aj,Bi) 的关系,但由于这是不可比性传递,
直接排序不满足严格弱序,还要加一维关键字,
观察 a 的前缀和对答案有一定的影响,把 a 更小的放前面是更优的,所以将 a 作为第二关键字。
Difficult Mountain
把所有登山者分成两类,一类是 ai<=si 的记为集合 S,一类是 si<ai 的记为集合 T,前者内部互不干扰,后者可以按照 ai 从小到大贪心。观察 S 对 T 的影响,对于 i属于S,j属于T,若 sj<ai<=si<aj,那么 i,j 之间只能选一个,因为 ai<aj 所以选 i 更优,其它情况下可以证明 i,j 可以同时选择。
以 max(ai,si) 为第一关键字,si 为第二关键字贪心即可。
证明技巧
打一个暴力程序,正解需要满足:
- 严格弱序
- 排序完成后任意交换相邻元素均不会使答案更优。
邻项交换
在可以通过比较相邻两项得出交换或不交换一定不会更差时,可以通过邻项交换排序的方式来得到最优解。
邻项交换排序的比较函数需要满足严格弱序,并且排序完成后任意交换相邻元素都不会更优。
使用这种算法时,一定要注意以上两点,才能得到真正正确的算法。

