Upd 初学线段树请不要看此文章，此文章仅停留在理论层次

$updata$ $2022/11/23$：更新了区间修改的暴力版本。
$updata$ $2024/02/24$：增加了对区间修改的解释。
$updata$ $2024/03/29$：感谢This User 提出的问题，修改了代码的锅。
$updata$ $2024/04/25$ 继续修改文中的细节，使其更加严谨

$1.$ 线段树简介

线段树是算法竞赛中常用的用来维护区间信息的数据结构。
线段树可以在很小的时间复杂度内实现单点修改、区间修改、区间查询（即区间求和，求区间 $\max$ ，求区间 $\min$ ，区间 $\gcd$ 等）操作。
但是，线段树所维护的信息，需要满足区间加法。
区间加法：如果一个区间 $[l,r]$（线段树中一个点表示一个区间）满足区间加法的意思是一个区间 $[l,r]$ 的线段树维护的信息（即区间最大值，区间最小值，区间和，区间 $\gcd$ 等），可以由两个区间 $[l,mid]$ 和 $[mid + 1,r]$ 合并而来。

$2.$ 线段树的基本概念

线段树，是一种基于分治思想的二叉搜索树。它支持的所有操作都可以 $O(\log n)$ 的时间复杂度完成。
线段树的基本特点：

1. 线段树的每一个节点表示一个区间
2. 线段树有唯一根，这个根表示的所有会被线段树统计的总区间，一般情况下，跟表示的区间就是 $[1,n]$
3. 线段树的叶子节点表示的区间为 $[x,x]$ ，且长度为 $1$
4. 线段树中如果一个节点表示的区间是 $[l,r]$ ，且这个点不为叶子节点，即 $l \not= r$，那么这个节点的左子树的根表示的区间就是 $[l,mid]$ 这个节点的右子树的根表示的区间就是 $[mid + 1,r]$，其中 $mid = ⌊\frac{l + r}{2}⌋$ 。
5. 线段树的题目可以调上一整天

Upd:其实不难，写多了就是模板。

$3.$ 线段树的存储方式

直接采用堆存储方式，即一颗线段树的跟的编号是 $1$ ，设一个不为根的节点编号 $x$ ，则这个点的父节点是 $⌊\frac{x}{2}⌋$ ，他的两个子节点的编号分别是 $2 × x$ 和 $2 × x + 1$ 。为了线段树的节点不超过存储范围，一般线段树都要开 $4 × n$ 的空间，即区间总长度的 $4$ 倍。
因为一颗线段树最多是一颗满二叉树，而满二叉树的最后一层是 $n$ 个点，前面的点数是 $n - 1$ ，所以一共要 $2 × n - 1$ 的空间，但由于线段树有可能最后一层节点还有子节点，比如说 $n = 10$ 的时候，如图：

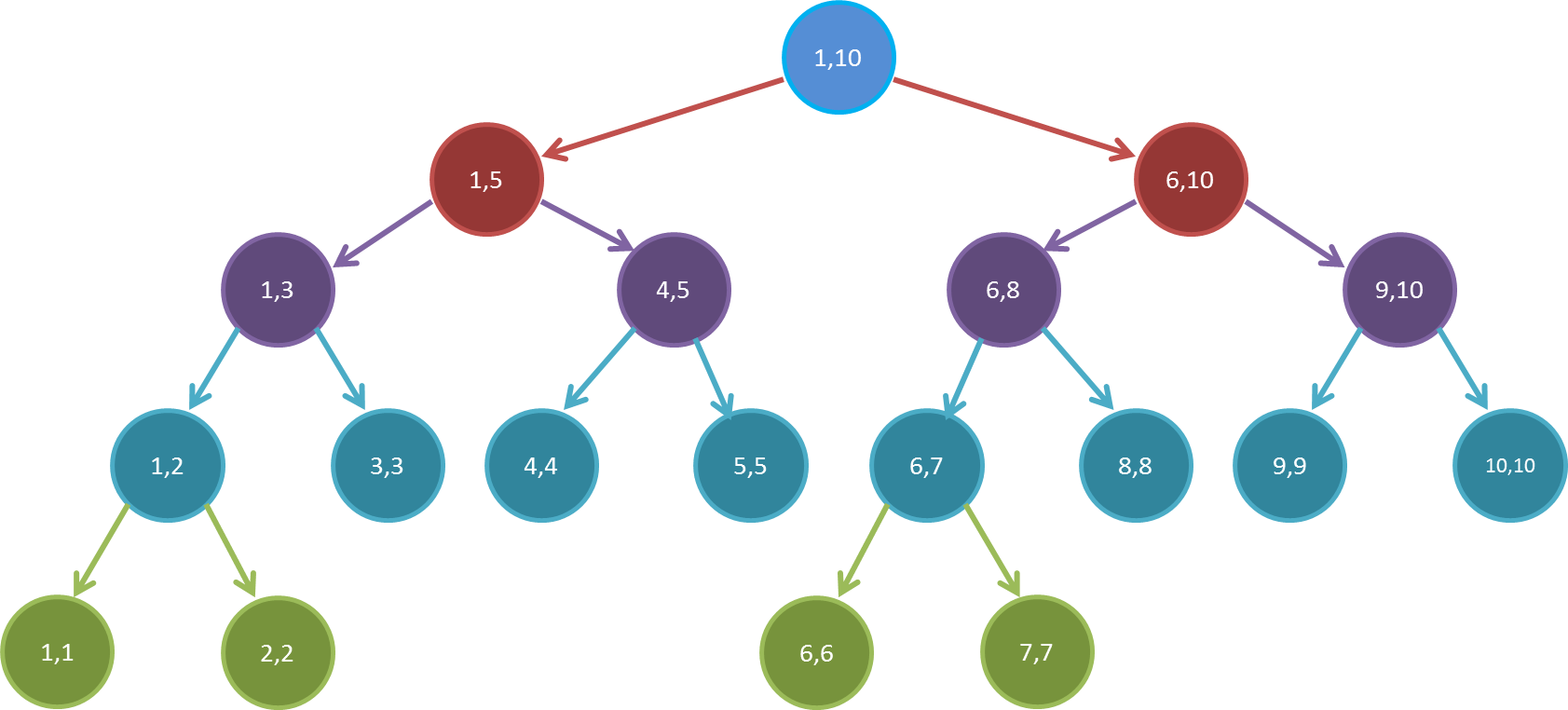
这里就是一个例子，最后一层是多出来的，而最后一层节点最多 $2 × n$ 个节点，最坏情况下就最右边两个节点，最右下角的一个节点的编号是 $2 × n - 1 + 2 × n = 4 × n - 1$ ，所以线段树一般开 $4 × n$ 。

$4.$建立线段树

思路

我们递归遍历初始区间，把遍历到的所有节点表示的区间记录下来，如果这个节点不是叶子节点（即区间长度大于$1$），那么就分别遍历左子树和右子树，否则就是叶子节点，不仅要把表示的区间记录下来，还要把线段树维护的信息也记录下来，维护的信息在叶子节点上基本上就是这个数本身。
时间复杂度 $O(n)$

代码

struct Segment_Tree {
    int l,r;
    info_type info;
    tag_type tag;
    //这里可以维护任何满足区间加法的信息
}tr[4 * N];   //要开四倍空间
//实现时可以写 info + info,info + tag,tag + tag 来简化代码
info_type operator + (info_type x,info_type y) {
    // 合并 info
}
info_type opreator + (info_type x,tag_type y) {
    // 合并 info 和 tag
}
tag_type operator + (tag_type x,tag_type y) {
    // 合并 tag
}
void opt (info_type &x,tag_type y) {
    x = x + y;
}
void push_up (int u) { 
    //这里举个例子，比如区间和，区间和就是由一个点的左右子节点的和相加
    //tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    tr[u].info = tr[u << 1].info + tr[u << 1 | !].info;
}
void build (int u,int l,int r) {  //当前正在下标为u的点，这个点表示的区间是[l,r]
    if (l == r) {
        tr[u] = {l,r,info (a[l])};
        return ;
    }
    tr[u] = {l,r};  //记得存储当前点表示的区间，否则你会调上一整天
    int mid = l + r >> 1;
    build (u << 1,l,mid),build (u << 1 | 1,mid + 1,r);  //u << 1就是u * 2，u << 1 | 1就是u * 2 + 1
    push_up (u);  //push_up函数的意思是把某一个节点的信息有他的子节点算出来
}

$5.$单点修改

思路

我们通过二分查找的形式找到要修改的点，然后把找的过程上的链都修改一下。
时间复杂度 $O(\log n)$

代码

void modify (int u,int x,tag_type d) {  
    if (tr[u].l == tr[u].r) {
        tr[u].info += d; //如果当前区间只有一个数，那么这个数一定是要修改的
        // 修改不局限于覆盖，也可能是别的
        return ;
    }
    int mid = tr[u].l + tr[u].r >> 1;
    if (x <= mid) modify (u << 1,x,d);  //如果在左边就递归修改左半边区间
    else modify (u << 1 | 1,x,d);    //如果在右边就递归修改右半边区间
    push_up (u)   //记得更新信息
}

$6.$区间修改

思路$1$

线段树的区间修改大体分为两步

1. 找到区间中全部都是要修改的点的线段树中的区间；
2. 修改这一段区间的所有点。

我们先解决第 $1$ 步：
我们从根节点（根节点一定包含所有点，既包含修改区间）出发，一直往下走，直到当前区间中的元素全部都是被修改元素。
当左区间包含整个被修改区间时，我们就递归到左区间；
当右区间包含整个被修改区间时，我们就递归到右区间；
否则区间的样子就如下图所示：

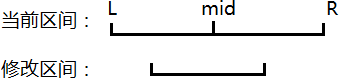
此时该怎么办呢？
不过，通过思考，我们可以发现，被修改区间中的元素间，两两之间都不会产生影响。
所以，我们可以把被修改区间分解成两段，使得其中的一段完全在左区间，另一端完全在右区间。
很明显，直接在 $mid$ 的位置将该区间切开是最好的。如下图所示：

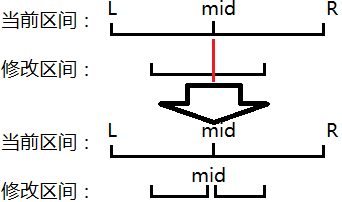
如果当前区间包含了修改区间的话就直接修改，把区间里的每一个数遍历一遍。
时间复杂度 $O(n)$

代码$1$

void modify (int u,int l,int r,tag_type d) {
    if (tr[u].l == tr[u].r) {   //叶子节点
        tr[u].info += d;
        return ;
    }
    int mid = tr[u].l + tr[u].r >> 1;  //注意是tr[u].l和tr[u].r
    if (l <= mid) modify (u << 1,l,r,d);  //左边有修改区间，就递归左半边
    if (r >= mid + 1) modify (u << 1 | 1,l,r,d);  //右边有修改区间，就递归右半边
    push_up (u);  //要记得要把这个点的信息更新一下
}

思路$2$

欸，你不是说线段树所有操作都是 $O(\log n)$ 的吗？现在怎么来了一个 $O(n)$ 的？
这不就是思路 $2$ 啊。。。
为提高线段树的修改效率，就要引入一个好东西：懒标记

懒标记就是我们在做修改操作时能用来偷懒的标记。

来自封禁用户（现 Conan15）的一个故事:

$A$ 有两个儿子，一个是 $B$，一个是 $C$。
有一天 $A$ 要建一个新房子，没钱。刚好过年嘛，有人要给 $B$ 和 $C$ 红包，两个红包的钱数相同都是 $1$ 元，然而因为 $A$ 是父亲所以红包肯定是先塞给 $A$ 咯~
理论上来讲 $A$ 应该把两个红包分别给 $B$ 和 $C$，但是……缺钱嘛，$A$ 就把红包偷偷收到自己口袋里了。
$A$ 高兴地说：「我现在有 $2$ 份红包了！我又多了 $2×1=2$ 元了！哈哈哈~」
但是 $A$ 知道，如果他不把红包给 $B$ 和 $C$，那 $B$ 和 $C$ 肯定会不爽然后导致家庭矛盾最后崩溃，所以 $A$ 对儿子 $B$ 和 $C$ 说：「我欠你们每人 $1$ 份 $1$ 元的红包，下次有新红包给过来的时候再给你们！这里我先做下记录……嗯……我欠你们各 $1$ 元……」
儿子 $B$ 、$C$ 有点恼怒：「可是如果有同学问起我们我们收到了多少红包咋办？你把我们的红包都收了，我们还怎么装？」
父亲 $A$ 赶忙说：「有同学问起来我就会给你们的！我欠条都写好了不会不算话的！」

至于懒标记：
如果父亲 $A$ 把钱给 $B$ 和 $C$ ，接着。。。 $A$ 就没钱了。没错！懒标记就是故事中的记录父亲 $A$ 没给的钱账本！
懒标记就是区间修改时偷懒用的，所以叫懒标记。
他主要解决了一个问题：如修改区间包含当前区间，就在这个节点上打个标记，表示这个点在以后的代码中要修改，现在先不修改。
懒标记的具体意思：我觉得 $y$ 总的懒标记意思比较好：如果一个点上打的一个懒标记，那么表示这个点的所有子节点都要变化这个懒标记（可以是加除 $\max$ ， $\min$ ， $\gcd$ 等等），注意！懒标记没有包含当前点！

$\text{Upd 2024/2/24}$

简单对懒标记再解释一下：
懒标记可以理解为修改标记，因为修改到的节点那么多，事实上以后用到的节点没有那么多。只有用到某一个节点，才进行修改。

其实后面用到的节点就是查询的节点，不论区间查询还是单点查询，用到的区间数量一定是 $O(\log _2 n)$ 的，所以我们只需要在遇到要查询或修改的区间时才修改懒标记对这个节点造成的变化。

代码$2$

void push_down (int u) { //下传标记函数
    if (tr[u].tag) {  //有懒标记才下传
        tr[u << 1].info += tr[u].tag,tr[u << 1 | 1].info += tr[u].tag
        tr[u].tag = info ();  //懒标记记得清零
    }
}
void modify (int u,int l,int r,int d) { //当前遍历到的点下标是u，要修改区间[l,r]
    if (l <= tr[u].l && tr[u].r <= r) {
        opt (u,d);
        return ;
    }
    push_down (u);  //一定要分裂，只要记牢在递归左右区间之前，就要分裂
    int mid = tr[u].l + tr[u].r >> 1;  //注意时tr[u].l和tr[u].r
    if (l <= mid) modify (u << 1,l,r,d);  //左边有修改区间，就递归左半边
    if (r >= mid + 1) modify (u << 1 | 1,l,r,d);  //右边有修改区间，就递归右半边
    push_up (u);  //要记得要把这个点的信息更新一下
}

$7.$区间查询

思路

区间查询类似区间修改，只不过变为查询了。

代码

LL query_sum (int u,int l,int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
    push_down (u);  //在递归之前一定要分裂
    int mid = tr[u].l + tr[u].r >> 1;
    LL sum = 0;
    if (l <= mid) sum += query_sum (u << 1,l,r);  //左半边有被查询到的数据，就递归左半边
    if (r >= mid + 1) sum += query_sum (u << 1 | 1,l,r);  //右半边有被查询到的数据，就递归右半边
    return sum;
}

时间复杂度 $O(\log n)$