Lucas 定理用于求解大组合数取模的问题
其中模数必须为素数。正常的组合数运算可以通过递推公式求解,但当问题规模很大,而模数是一个不大的质数的时候,就不能简单地通过递推求解来得到答案,需要用到 Lucas 定理。
定理描述及其证明过程如下(主要运用生成函数和p进制转化的思想):


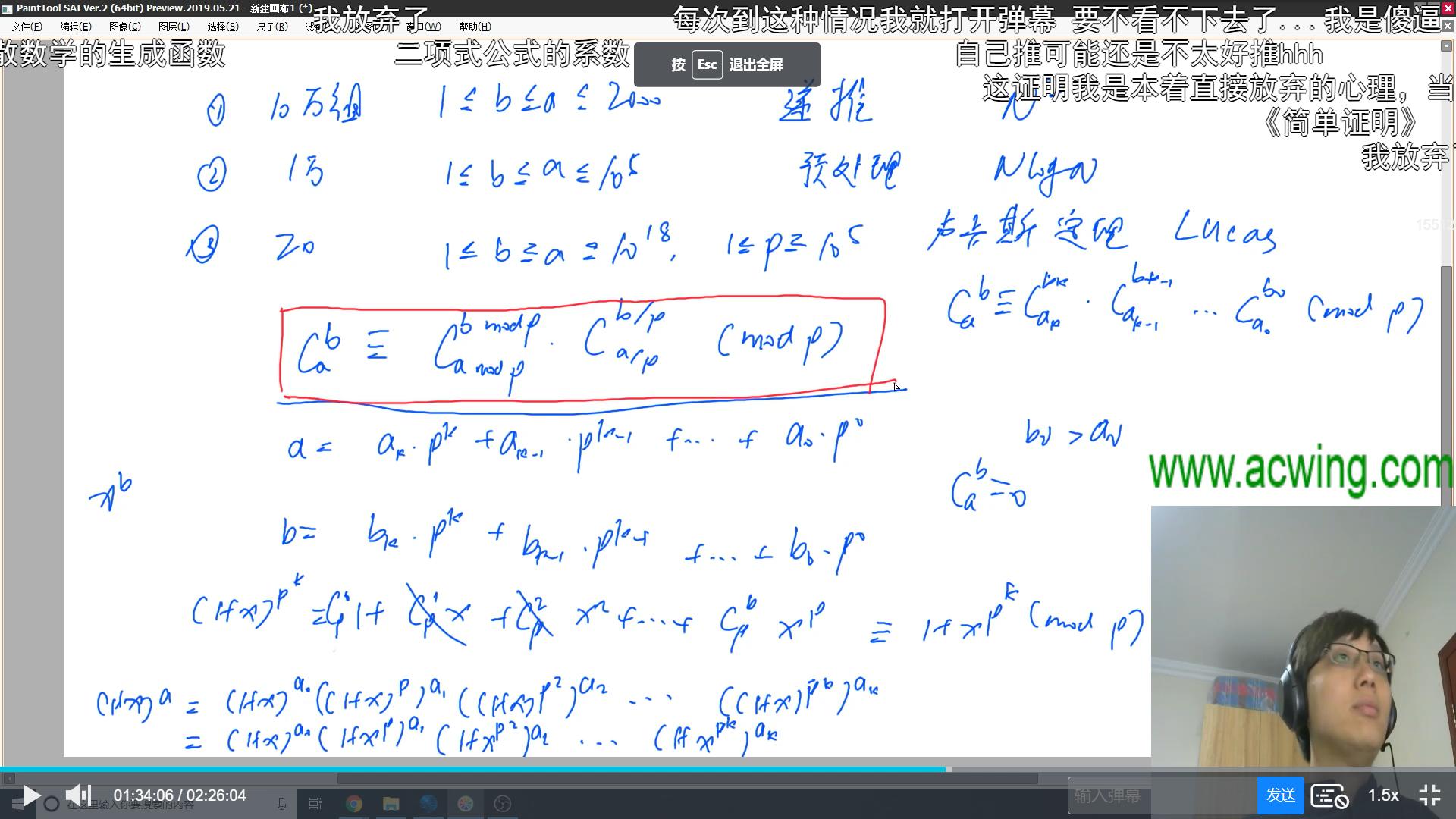
模板题目链接
###参考代码如下
#include<stdio.h>
#include<iostream>
#define ll long long
using namespace std;
int p;
int qmi(int a,int b,int p)
{
int res=1%p;
while(b)
{
if(b&1)res=(ll)res*a%p;
b>>=1;
a=(ll)a*a%p;
}
return res;
}
int C(int a,int b)
{
b=min(b,a-b);
if(b<0)return 0;
int res=1;
for(int i=1,j=a;i<=b;i++,j--)
res=(ll)res*j%p*qmi(i,p-2,p)%p;
return res;
}
int lucas(ll a,ll b)
{
if(a<p && b<p)return C(a,b);
else return (ll)C(a%p,b%p)*lucas(a/p,b/p)%p;
}
int main()
{
int n;
ll a,b;
scanf("%d",&n);
while(n--)
{
scanf("%lld%lld%d",&a,&b,&p);
printf("%d\n",lucas(a,b));
}
return 0;
}
需要注意的是,lucas定理仅用于模数为质数的情况。若模数为质数,组合数巨大无比,那么应使用扩展Lucas定理(主要是lucas+CRT中国剩余定理)。
看参考以下文章
lucas及其扩展

