有向图：所有边都有方向
无向图：所有边都是双向的
入度：有向图顶点的入边条数
出度：有向图顶点的出边条数

图的存储：

1. 邻接矩阵存储
2. 邻接表
   单链表 （每个点都开一个单链表） 同一个顶点的所有出边放在一个单链表中

//邻接表实现
int h[N],e[N],ne[N],idx;
//插入一个结点
void add(int a,int b){//单链表
    e[idx] = b;
    ne[idx]  = h[a];
    h[a] = idx++;
}
for(int i=0;i<n-1;i++){
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);
    }

vector 实现

vector<int> v[N];
for(int i=0;i<n-1;i++){
        int a,b;
        cin>>a>>b;
        //添加从a号顶点到b号顶点的边   从b号顶点到a号顶点的边
        v[a].push_back(b),v[b].push_back(a);
    }

图的遍历：

深度优先搜索遍历DFS

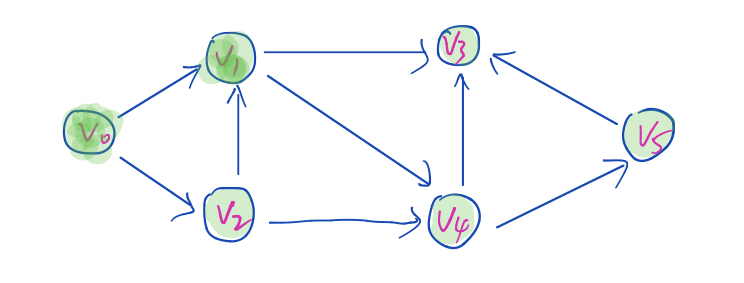
V0 ----- > V1 --------> V3 此时发现从V3出发到不了任何点，所以返回到当前路劲上距离V3最近的仍有未访问分支顶点的岔道口，
此时返回到V1，发现还可以到达V4 则 继续 ------>V4 ----->V5
此时从V5出发到达不了任何未访问顶点，所以返回到当前路劲上距离V5最近的仍有未访问分支顶点的岔道口，
此时返回到V0, 则继续 -----> V2 V2出发没有任何未访问点可以到达，则返回， 且路径上所有分支顶点均已被访问，所以至此结束
综上：遍历路径为：V0 ----- > V1 --------> V3 ------>V4 ----->V5-----> V2

//深度优先遍历图
void dfs(int u){
    st[u] = true;//标记已经被搜索过
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        if(!st[j]) dfs(j);
    }
}

宽度优先搜索BFS遍历

每次以扩散的方式 向外访问顶点
用队列queue来实现：
每次取出对头元素，将拓展出的所有元素放到队尾

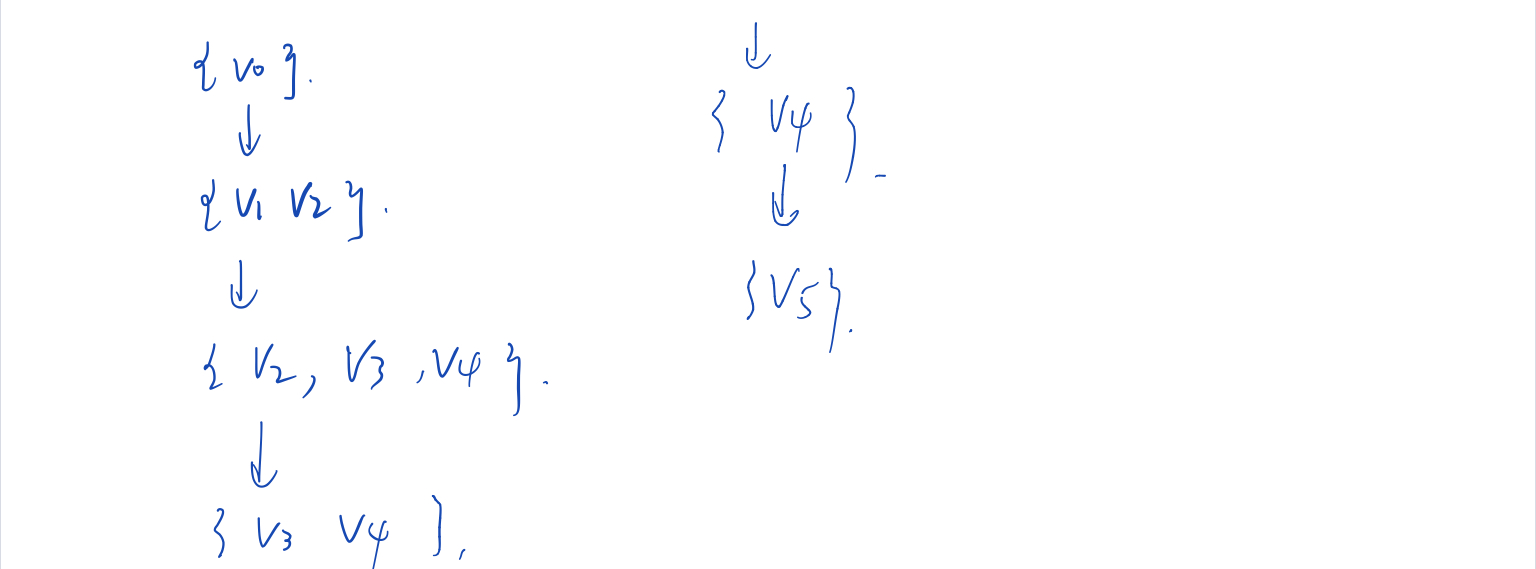
while(q非空)
    取出对头元素t
    for(从t扩展出的所有顶点v){
        if(v没有加入队列){
            将v入队
            标记v已加入队列
        }
    }

bool st[N];
void BFS(int u){
    queue<int> q;
    q.push(u);//初始点加入队
    st[U]=true;
    while(!q.empty()){
        int t = q.front();
        q.pop();
        for(int i=h[t];i!=-1;i = ne[i]){
            int j = e[i];
            if(st[j] == false){
                q.push(j);
                st[N] = true;
            }
        }
    }
}