历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

排序算法整理

作者：

incra , 2022-08-22 11:29:41 , 所有人可见 , 阅读 1100

37

28

本文由于本人~~太菜了~~，借鉴了许多题解的内容，在此表示感谢。

十种常见排序算法

十种常见排序算法可以分为两大类：

比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破 $O(n\log n)$ ，因此也称为非线性时间比较类排序。包括插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序和归并排序。
非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。包括计数排序、桶排序和基数排序。

排序算法时间复杂度

比较类排序算法

排序算法名称	平均时间复杂度	最坏时间复杂度	最好时间复杂度	空间复杂度	稳定性
冒泡排序	$θ(n^2)$	$O(n^2)$	$Ω(n^2)$	$O(1)$	稳定
插入排序	$θ(n^2)$	$O(n^2)$	$Ω(n)$	$O(1)$	稳定
希尔排序	$θ(n^d)$ $d≈1.5$	$O(n^2)$	$Ω(n)$	$O(1)$	不稳定
选择排序	$θ(n^2)$	$O(n^2)$	$Ω(n^2)$	$O(1)$	不稳定
堆排序	$θ(n\log n)$	$O(n\log n)$	$Ω(n\log n)$	$O(1)$	不稳定
快速排序	$θ(n\log n)$	$O(n^2)$	$Ω(n\log n)$	$O(n\log n)$	不稳定
归并排序	$θ(n\log n)$	$O(n\log n)$	$Ω(n\log n)$	$O(n)$	稳定

非比较类排序算法

排序算法名称	平均时间复杂度	最坏时间复杂度	最好时间复杂度	空间复杂度	稳定性
计数排序	$θ(n+k)$	$O(n+k)$	$Ω(n+k)$	$O(n+k)$	稳定
桶排序	$θ(n+k)$	$O(n^2)$	$Ω(n)$	$O(n+k)$	稳定
基数排序	$θ(n×k)$	$O(n×k)$	$Ω(n×k)$	$O(n+k)$	稳定

1冒泡排序$(Bubble-Sort)$

1.1算法流程

我们遍历数组至多 $n$ 次，（那是已经排好序了）每次判断相邻两个数前一个是否大于后一个，如果大于后一个，就交换，否则不变。

1.2动图演示

1.3代码

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= n - i - 1;j++) {
            if (a[j] > a[j + 1]) swap (a[j],a[j + 1]);
        }
    }
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

2插入排序$(Insertion-Sort)$

2.1算法流程

我们把未排序的数中的第一个数放到它该放在的位置（即前一个数小于它并且后一个数大于它的位置）。执行 $n$ 次，就能得到排好序的数组。

2.2动图演示

2.3代码

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    for (int i = 1;i <= n;i++) {
        for (int j = i - 1;j >= 1 && a[j] > a[j + 1];j--) swap (a[j + 1],a[j]);
    }
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

3希尔排序$(Shell-Sort)$

3.1算法流程

选择一个增量序列 $t_1,t_2,…,t_k$ 其中 $t_i > t_j$ 且 $t_k = 1$ 。
按增量序列个数 $k$ ，对序列进行 $k$ 趟排序；
每趟排序，根据对应的增量 $t_i$ ，将待排序列分割成若干长度为 $m$ 的子序列，分别对各子表进行直接插入排序。仅增量因子为 $1$ 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
这里当 $\forall~i\in[2,n]$ ，都有 $a_i = a_{i-1}\times3+1$ 时，速度最快。

3.2动图演示

3.3代码

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    int gap = 1;
    while (gap < n / 3) gap = gap * 3 + 1;
    while (gap) {
        for (int i = gap;i <= n;i++) {
            for (int j = i;j >= gap && a[j - gap] > a[j];j--)swap (a[j - gap],a[j]);
        }
        gap /= 3;
    }
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

4选择排序$(Selection-Sort)$

4.1算法流程

首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到第二个位置。以此类推，直到所有元素均排序完毕。

4.2动图演示

4.3代码

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    for (int i = 1;i <= n;i++) {
        int pos = i;
        for (int j = i;j <= n;j++) {
            if (a[j] < a[pos]) pos = j;
        }
        swap (a[i],a[pos]);
    }
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

5堆排序$(Heap-Sort)$

5.1算法流程

堆存储的数据具有单调性，每次取出堆的最小值放到数组中，再从堆里删除这个数，执行 $n$ 次后，数组就是排好序的数组。

5.2动图演示

5.3代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n,m;
int h[N],s;
void down (int u) {
    int t = u;
    if (u * 2 <= s && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= s && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) {
        swap (h[u],h[t]);
        down (t);
    }
}
int main () {
    cin >> n >> m;
    for (int i = 1;i <= n;i++) cin >> h[i];
    s = n;
    for (int i = n / 2;i >= 1;i--) down (i);
    while (m--) {
        cout << h[1] << ' ';
        h[1] = h[s--];
        down (1);
    }
    return 0;
}

6快速排序$(Quick-Sort)$

6.1算法流程

我们分别从数组的最前面和最后面枚举两个变量，再选一个数作为标准，如果左边的变量只想的数大于标准并且右边的变量指向的数小于标准的话，就叫唤这两个数。等到执行完了（即左边的变量跑到右边的变量的右边去了），就分别递归排序两边。

6.2动图演示

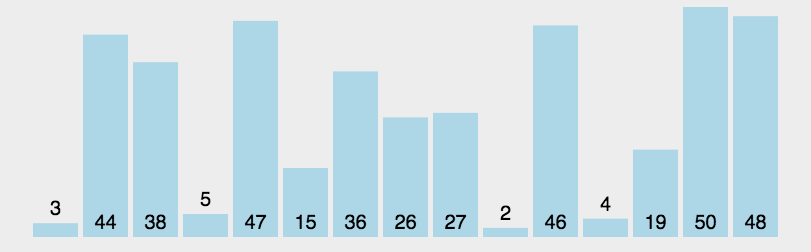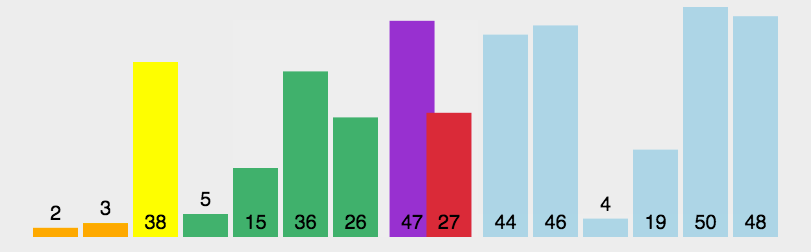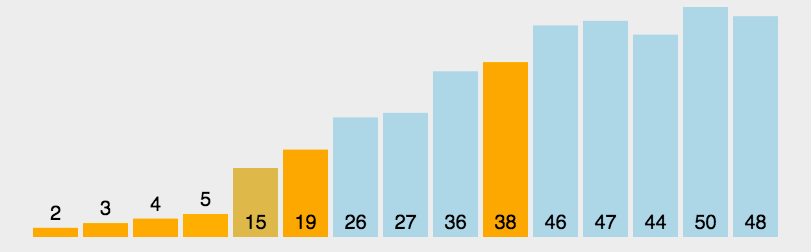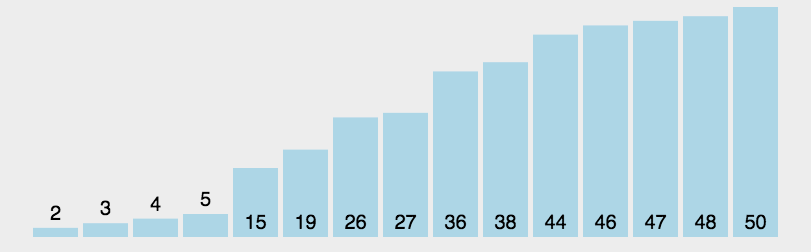
6.3代码

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
void quickSort (int a[],int l,int r) {
    if (l >= r) return ;
    int x = a[(l + r + 1)/2],i = l - 1,j = r + 1;  //这里取中间的话要取(l + r + 1) / 2，否则会超时
    while (i < j) {
        do i++; while (a[i] < x);
        do j--; while (a[j] > x);
        if (i < j) swap (a[i],a[j]);
    }
    quickSort (a,l,i - 1),quickSort (a,i,r);
}
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    quickSort (a,1,n);
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

7归并排序$(Merge-Sort)$

7.1算法流程

把一段数组从中间分开，左边和右边分别执行归并排序，执行好后把左右的有序数组归并成一个。

7.2动图演示

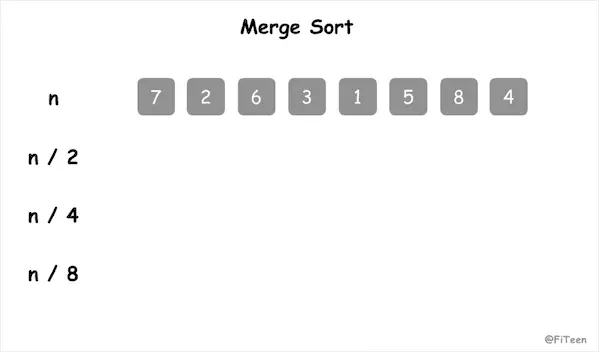
7.3代码

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N],tmp[N];
void mergeSort (int a[],int l,int r) {
    if (l >= r) return ;
    int mid = l + r >> 1;
    mergeSort (a,l,mid),mergeSort (a,mid + 1,r);
    int k = 1,i = l,j = mid+1;
    while (i <= mid && j <= r) {
        if (a[i] <= a[j]) tmp[k++] = a[i++];
        else tmp[k++] = a[j++];
    }
    while (i <= mid) tmp[k++] = a[i++];
    while (j <= r) tmp[k++] = a[j++];
    for (i = l,j = 1;i <= r;i++,j++) a[i] = tmp[j];
}
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    mergeSort (a,1,n);
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

8计数排序$(Counting-Sort)$

8.1算法流程

统计每个数的数量，最后按序取出即可。

8.2动图演示

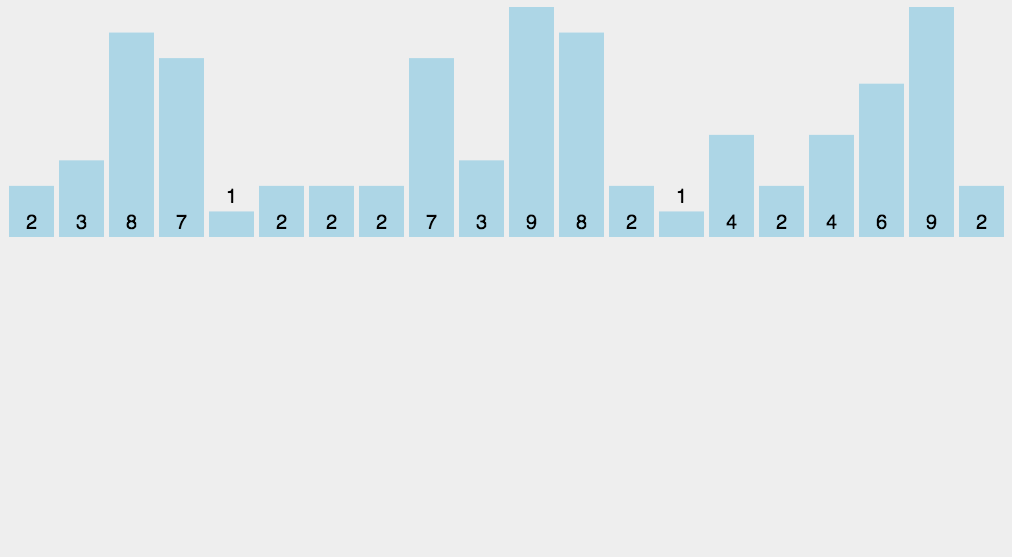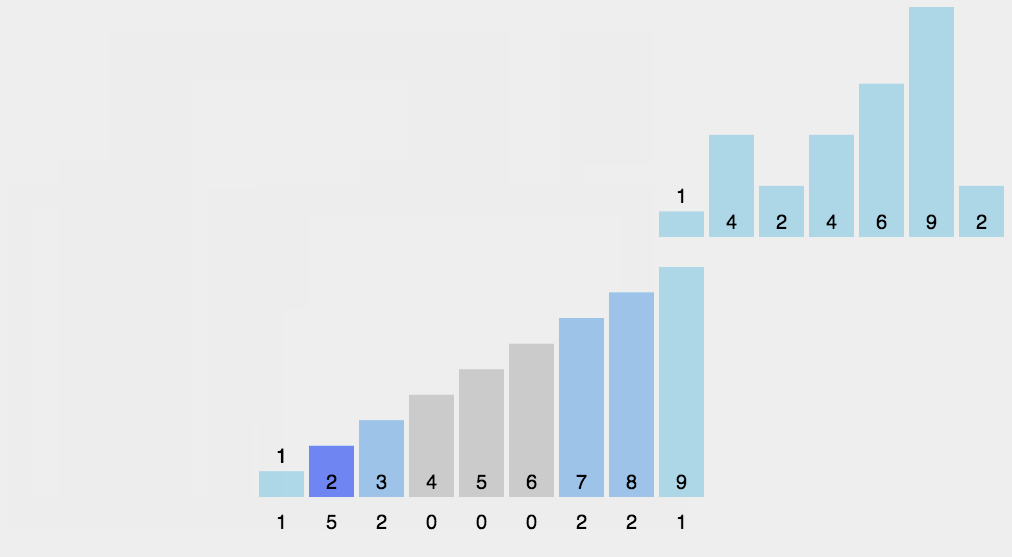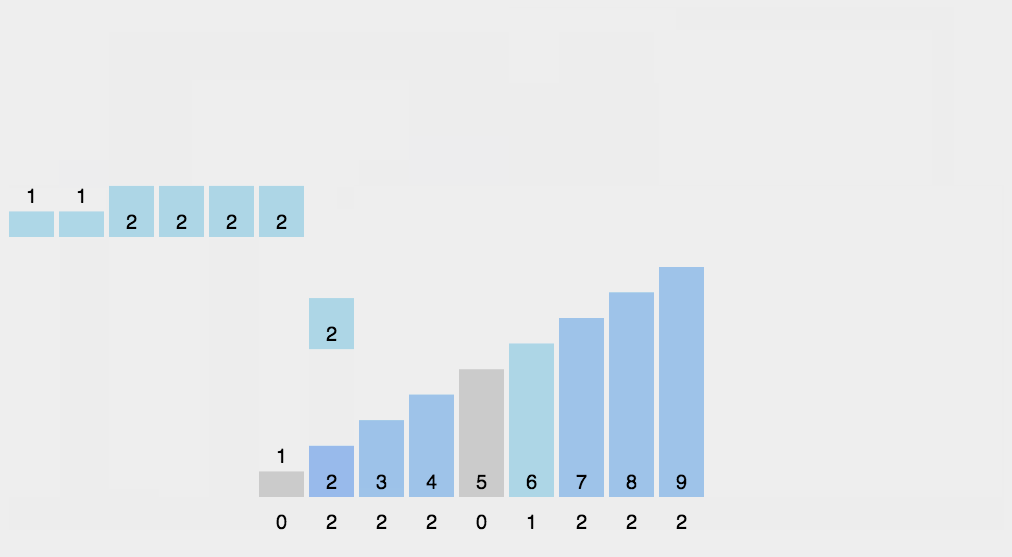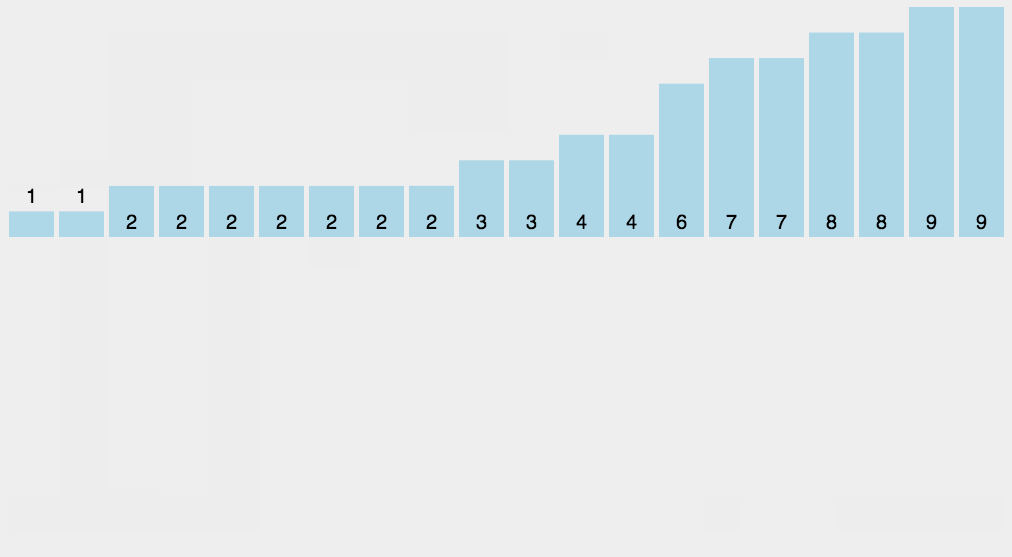
8.3代码

#include <iostream>
using namespace std;
const int N = 100010,M = 100000010;
int n;
int cnt[M];
int main () {
    cin >> n;
    int minx = 2e9,maxx = -2e9;
    for (int i = 1;i <= n;i++) {
        int x;
        cin >> x;
        cnt[x]++;
        minx = min (minx,x),maxx = max (maxx,x);
    }
    for (int i = minx;i <= maxx;i++) {
        while (cnt[i]--) cout << i << ' ';
    }
    return 0;
}

9桶排序$(Bucket-Sort)$

9.1算法流程

把所有数据分成几个桶，每个桶里分别用独自的排序算法（如冒泡排序，插入排序都可以）。

9.2动图演示

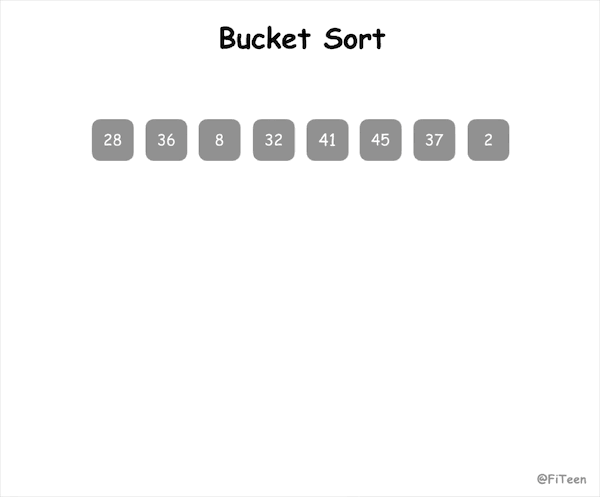
9.3代码

#include <iostream>
#include <vector>
using namespace std;
const int N = 100010;
int n;
int a[N];
int minx,maxx;
int bucket_cnt = 40;
vector <int> bucket[50];
void bubble_sort (int x) {
    int m = bucket[x].size ();
    for (int i = 0;i < m;i++) {
        for (int j = 0;j < m - i - 1;j++) {
            if (a[j] > a[j + 1]) swap (a[j],a[j + 1]);
        }
    }
}
int main () {
    cin >> n;
    minx = 2e9,maxx = -2e9;
    for (int i = 1;i <= n;i++) {
        cin >> a[i];
        minx = min (minx,a[i]),maxx = max (maxx,a[i]);
    }
    for (int i = 1;i <= n;i++) {
        int t = (a[i] - minx) / ((maxx - minx + 1) / 40.0);
        bucket[t].push_back (a[i]);
    }
    for (int i = 0;i <= bucket_cnt;i++)  {
        if (bucket[i].size ()) bubble_sort (i);  //这里可以用任意排序算法，这里就用冒泡排序了
    }
    for (int i = 0;i <= bucket_cnt;i++) {
        for (int j = 0;j < bucket[i].size ();j++) cout << bucket[i][j] << ' ';
    }
    return 0;
}

10基数排序$(Radix-Sort)$

10.1算法流程

我们把所有数先按个位放进十个桶，（按个位数的大小，比如各位是 $0$ ，就放在编号为 $0$ 的桶），然后按先放入的先取出，（即 $FIFO$ ，否则就不仅不稳定了，还可能破坏顺序）接着再按十位排序，（注意没有十位用 $0$ 表示，更高位也是这样）再按按先放入的先取出。一直到所有数的这一位都是 $0$ ，就可以退出了。

10.2动图演示

10.3代码

#include <iostream>
#include <vector>
using namespace std;
const int N = 100010;
int n;
int a[N];
vector <int> bucket[10];
int main () {
    cin >> n;
    int maxx = -2e9;
    for (int i = 1;i <= n;i++) {
        cin >> a[i];
        maxx = max (maxx,a[i]);
    }
    int radix = 1;
    while (radix <= maxx) {
        for (int i = 0;i <= 9;i++) bucket[i].clear ();
        for (int i = 1;i <= n;i++) bucket[a[i] / radix % 10].push_back (a[i]);
        int k = 1;
        for (int i = 0;i <= 9;i++) {
            for (int x : bucket[i]) a[k++] = x;
        }
        radix = radix * 10;
    }
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

不常见排序算法

排序算法名称	平均时间复杂度	最坏时间复杂度	最好时间复杂度	空间复杂度	稳定性
鸡尾酒排序	$θ (n^2)$	$O(n^2)$	$Ω(n)$	$O (1)$	稳定
猴子排序	$θ (+∞)$	$O(+∞)$	$Ω(n)$	$O (1)$	不稳定
珠排序	$θ(\sqrt n)$	$O(\sqrt n)$	$Ω(\sqrt n)$	$unknow$	$unknow$

1鸡尾酒排序 $(cocktail-sort)$

1.1算法流程

类似与冒泡排序。只有一点不同：如果在第奇数次遍历，就从前往后遍历，否则就从后往前遍历

1.2代码

#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    for (int i = 1;i <= n;i++) {
        if (i & 1) {
            for (int j = 1;j <= n - i - 1;j++) {
                if (a[j] > a[j + 1]) swap (a[j],a[j + 1]);
            }
        }
        else {
            for (int j = n - i - 1;j >= 1;j--) {
                if (a[j] > a[j + 1]) swap (a[j],a[j + 1]);
            }
        }
    }
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

2猴子排序 $(bogo-sort)$

2.1算法流程

随机打乱数组，有 $\cfrac{1}{n!}$ 的概率会变有序，但不要用这个排序，否则你会后悔的。。。

2.2代码

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int n;
int a[N];
bool check () {
    for (int i = 1;i <= n - 1;i++) {
        if (a[i] > a[i + 1]) return false;
    }
    return true;
}
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) cin >> a[i];
    while (!check ()) random_shuffle (a + 1,a + 1 + n);
    for (int i = 1;i <= n;i++) cout << a[i] << ' ';
    return 0;
}

3珠排序

3.1算法流程

需要特别硬件

3.2代码

需要特别硬件

15 评论

时来天地皆同力 2022-09-14 21:06

快排的空间复杂度和冒泡的最好时间复杂度是不是有点问题。

incra 2022-11-01 16:56

你仔细描述下

时来天地皆同力 2022-11-16 14:51 回复了 incra 的评论

快排的空间复杂度应该是 $log n$ 吧. 并且对于冒泡排序来讲，当原本顺序就是排好的情况下，其实就遍历了一次. 最好的时间复杂度为$O(n)$, 不过要加个额外的flag变量进行判断.

云衣醉梦 2022-09-12 15:37

%%%%%%%%%Orz

sentimental 2022-08-27 11:32

$珠排序是O(n^3)$

incra 2022-08-27 18:17

???我记得是 $O(\sqrt n)$

晓月兮清风 2023-04-23 16:35 回复了 incra 的评论

珠排序理论O(1), 实际O(N^2) (狗头保命

incra 2023-04-23 19:12 回复了晓月兮清风的评论

不一定吧

晓月兮清风 2023-04-25 17:57 回复了 incra 的评论

是啊，在现实中确实是O(1), 电脑中是模拟的，需要将“珠数组”遍历一遍，O(N^2)

incra 2023-04-25 18:14 回复了晓月兮清风的评论

addd

陆修远 2022-08-22 17:09

希尔排序是$O(n^{{4}\over{3}})$吧

incra 2022-08-22 17:22

好像都可以hh

陆修远 2022-08-22 18:37 回复了 incra 的评论

如果是$1e6$这种数据那不就差距很大吗？

冰中月 2022-09-04 09:24 回复了 incra 的评论

平均好像是$O(n^{1.25})$，似乎

晓月兮清风 2023-04-23 16:33 回复了冰中月的评论

n^1.3吧, 看每次分的组，根据希尔本人的，应该是N^1.3

App 内打开

排序算法整理

十种常见排序算法

十种常见排序算法可以分为两大类：

排序算法时间复杂度

比较类排序算法

非比较类排序算法

相关概念

1冒泡排序$(Bubble-Sort)$

1.1算法流程

1.2动图演示

1.3代码

2插入排序$(Insertion-Sort)$

2.1算法流程

2.2动图演示

2.3代码

3希尔排序$(Shell-Sort)$

3.1算法流程

3.2动图演示

3.3代码

4选择排序$(Selection-Sort)$

4.1算法流程

4.2动图演示

4.3代码

5堆排序$(Heap-Sort)$

5.1算法流程

5.2动图演示

5.3代码

6快速排序$(Quick-Sort)$

6.1算法流程

6.2动图演示

6.3代码

7归并排序$(Merge-Sort)$

7.1算法流程

7.2动图演示

7.3代码

8计数排序$(Counting-Sort)$

8.1算法流程

8.2动图演示

8.3代码

9桶排序$(Bucket-Sort)$

9.1算法流程

9.2动图演示

9.3代码

10基数排序$(Radix-Sort)$

10.1算法流程

10.2动图演示

10.3代码

不常见排序算法

1鸡尾酒排序 $(cocktail-sort)$

1.1算法流程

1.2代码

2猴子排序 $(bogo-sort)$

2.1算法流程

2.2代码

3珠排序

3.1算法流程

3.2代码

15 评论