关于上次一张小讲义的最后一题(即本笔记后面的例一)，这道题其实有通用解法，再也不用转化为等效电路，不用浪费脑细胞，不用管有没有电桥，只需设几个变量，列个方程全部搞定，童叟无欺，快乐无脑……

先介绍一个“小”定律

基尔霍夫第一定律

对于闭合电路中任意一点，恒有汇入电流等于汇出电流，即
$$ \sum I_入=\sum I_出 $$

如：对于图中电路，有：$I_1+I_2=I_3$

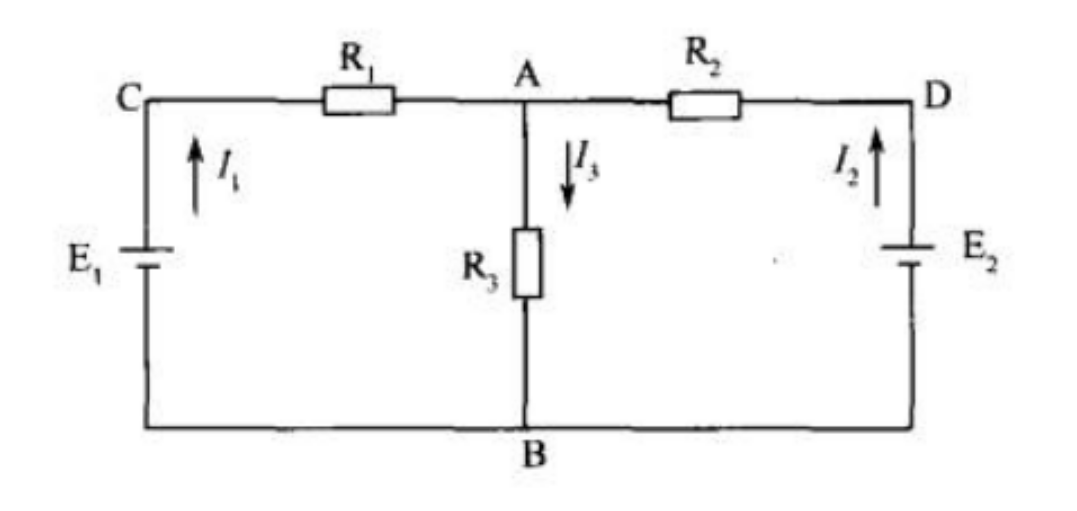
本解法整体思路：

设出图中各节点电势，用上述电流之间的关系列出方程，最后求出所需的量。

例一

由于电流从$O$点流入，$D$点流出，因此设$O$点电势为$U$(设成$1$也行)，$D$点电势为$0$.
如下图，红色箭头为电流方向：

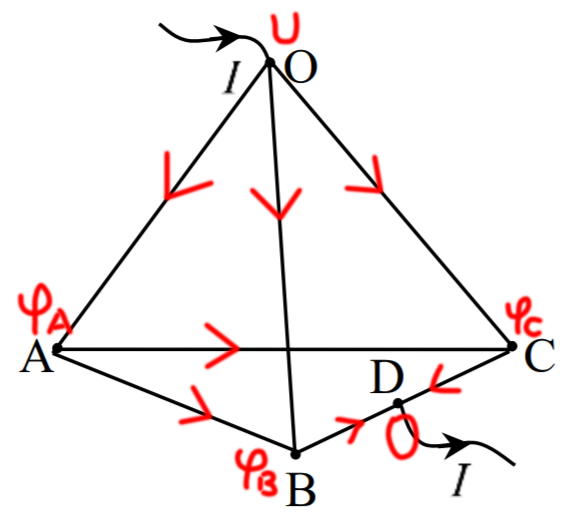
显然，此时$OA$段电流为$\large{\frac{U-\phi_A}{r}}$，其他段也同理，
于是可列出如下方程组：

$ \left\\{ \begin{aligned} 对A点：\frac{U-\phi_A}{r} = & \frac{\phi_A-\phi_B}{r} + \frac{\phi_A-\phi_C}{r}\\\ 对B点：\frac{U-\phi_B}{r} + & \frac{\phi_A-\phi_B}{r} = \frac{\phi_B-0}{\frac r2}\\\ 对C点：\frac{U-\phi_C}{r} + & \frac{\phi_A-\phi_C}{r} = \frac{\phi_C-0}{\frac r2}\\\ \end{aligned} \right. $

解得：$ \left\\{ \begin{aligned} \phi_A = & \frac 35 U\\\ \phi_B = & \phi_C = \frac 25 U\\\ \end{aligned} \right. $

以及最后一道方程确定$U、I$和$r$的关系：

$ \begin{aligned} 对O点：I = & \frac{U-\phi_A}{r} + \frac{U-\phi_B}{r} + \frac{U-\phi_C}{r}\\\ \end{aligned} $

解得：$ \begin{aligned} \frac Ur = \frac 58 I \end{aligned} $

解完方程组再回来看问题
$AB$段电流为$\large{\frac{\phi_A-\phi_B}{r}} = \frac 18 I$
$OD$段等效电阻即为$\large{\frac UI = \frac 58 r}$

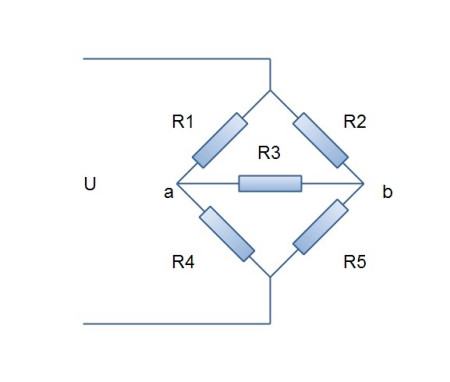
例二：

如图，$U=12V, R1=R2=10\Omega, R3=R4=5\Omega, R5=2\Omega$，求经过$R3$的电流$I$大小.

同理，假设电流从上方流到下方，流入点电势为$U$，流出点电势为$0$，
本题由于不确定流过$R3$的电流方向，因此随便假设一个方向，最后算出来的电势一定是对的。此处假设$R3$处电流像左

列方程：$ \left\\{ \begin{aligned} 对a点：\frac{U-\phi_a}{R1} + & \frac{\phi_b-\phi_a}{R3} = \frac{\phi_a-0}{R4}\\\ 对b点：\frac{U-\phi_b}{R2} = & \frac{\phi_b-\phi_a}{R3} + \frac{\phi_b-0}{R5}\\\ \end{aligned} \right. $

解得：$ \left\\{ \begin{aligned} \phi_a = & \frac{10}{3}\\\ \phi_b = & \frac{21}{9}\\\ \end{aligned} \right. $

故$\large{I = \frac{|\phi_a - \phi_b|}{R3} = 0.2A}$

PS:本解法源自竞赛，但由于实在简单好用，就介绍给大家了。