状态机模型

状态机是一个数学模型，数学符号描述为 $$M=(\varSigma, S, s_{0}, \delta, F)$$ 其中

• $\varSigma$ :输入表
• $S$ ：状态的非空有限集合
• $s_{0}$ ：初始状态，是 $S$ 的元素
• $\delta$ ：状态转移函数，$\delta:S\times \varSigma \to S$
• $F$ ：最终状态的集合，是 $S$ 的子集

该数学模型描述的是一个抽象的对象有许多状态，组成集合 $S$ 。该对象初始状态为 $s_{0}$ ,然后对象接收输入 $\varSigma$ 。每次接收输入后，对象都按照状态转移函数 $\delta$ 变换当前状态。

以上状态机的描述不是确切的描述，但是对于解题基本足够

根题

AcWing 285. 没有上司的舞会

隐藏的一个树上的状态机模型

例题

AcWing 1049. 大盗阿福

闫氏DP分析法

• 状态表示 f[i]
  • 集合：从前 $i$ 家店铺抢劫的所有方案
  • 属性：Max
• 状态计算
  • 集合划分
    - 抢第 $i$ 家店铺：f[i - 2] + w[i]
    - 不抢第 $i$ 家店铺：f[i-1]
  • 转移方程：f[i] = max(f[i - 1], f[i - 2] + w[i])

按照上述的DP分析法，需要用到 f[i-2] 的信息。如何才能只依赖 f[i - 1] 的信息？

在本题中，当前物品选与不选的操作受之前物品选与不选的操作的影响，而之前做过的DP题不存在这种关系限制（没有上司的舞会除外）。因此引入状态和状态机，状态存储的就是前面商铺被抢劫的信息

f[i] 可以分解为两种状态：

• f[i,0] :未选当前店铺
• f[i,1] :选择当前店铺

状态机描述：

• 初始状态为 $0$
• 当状态为 $0$ 时
  • 不抢：继续为 $0$
  • 抢：状态变为 $1$
• 当状态为 $1$ 时，不能抢，只能不抢，变为 $0$

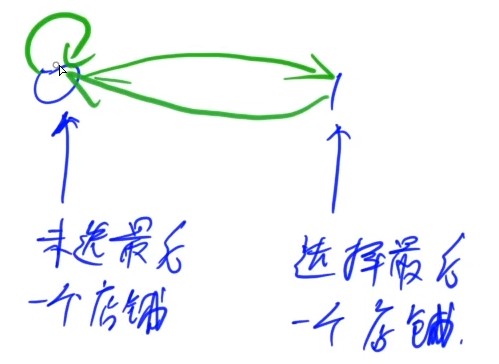
每一个店都要在状态机模型上走一条边，因此任何一个抢劫方案都能对应状态机上一个长度为 $n$ 的走法

闫氏DP分析法之状态机分析法

• 状态表示 f[i,0] f[i,1]
  • 集合：所有走了 $i$ 步，且当前位于状态 $j$ 的所有走法
  • 属性：Max
• 状态计算：按照状态机的描述来转移状态
  • f[i, 0] = max(f[i - 1, 0], f[i - 1, 1])
  • f[i ,1] = f[i - 1, 0] + w[i]
• 初始化：f[0, 0] = 0, f[0, 1] 不会被用到

1049代码

AcWing 1057. 股票买卖 IV

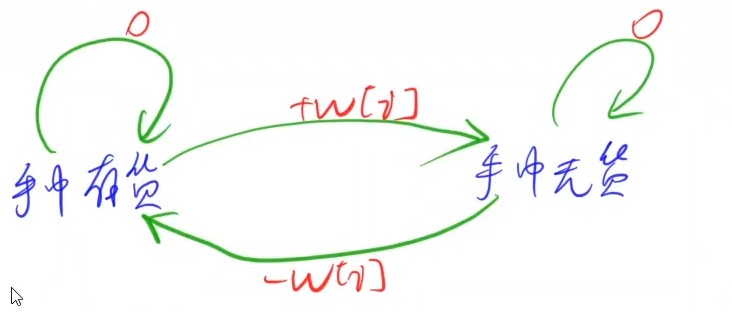
状态机中有两种状态，状态变换的边有权重，为每次状态变换的收益

• 手中有货
  • 可以继续持有，权重为 $0$，状态继续为手中有货
  • 可以卖出，权重为 $+w_{i}$，状态变为手中无货
• 手中无货
  • 可以不买货，权重为 $0$ ，状态继续为手中无货
  • 可以买入，权重为 $-w_{i}$ ，状态变为手中有货
• 起始状态：手中无货
• 结束状态：手中无货或有货，但无货肯定比有货获得收益更优

闫氏DP分析法之状态机分析法

• 状态表示 f[i, j, 0] f[i, j, 1] ：只考虑前 $i$ 天，已经进行完前 $j-1$ 次交易
  • f[i, j, 0] ：表示已经进行完了第 $j$ 次交易，手中无货
  • f[i, j, 1] ：表示正在进行第 $j$ 次交易，手中有货
• 状态计算
  • f[i, j, 0] = max(f[i - 1, j, 0], f[i - 1, j, 1] + w[i])
  • f[i, j, 1] = max(f[i - 1, j, 1], f[i - 1, j - 1, 0] - w[i])
• 初始化：$j$ 是一个正好的状态，因此先全部初始化为无穷。根据实际意义，f[i, 0, 0] = 0, f[i, 0, 1]不存在 。因为已经先全部初始化为无穷了，就只用将 f[i, 0, 0] 初始化为 $0$ 即可

1057代码

AcWing 1058. 股票买卖 V

与上一题的变化：没有交易次数的限制，但有交易冷却期

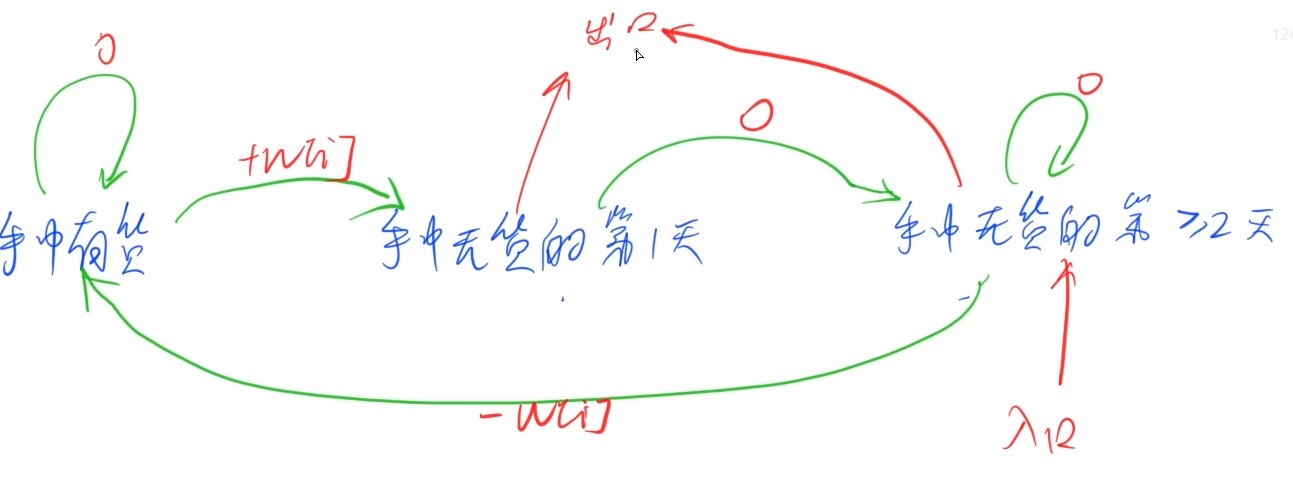
状态机中有三种状态

• 手中有货
  • 可以继续持有，权重为 $0$ ，状态继续为手中有货
  • 可以卖出，权重为 $+w_{i}$ ，状态变为手中无货的第 $1$ 天
• 手中无货的第 $1$ 天
  • 不能买入，权重为 $0$ ，状态变为手中无货的第 $\geq 2$ 天
• 手中无货的第 $\geq 2$ 天
  • 可以不买入，权重为 $0$ ，状态继续为手中无货的第 $\geq 2$ 天
  • 可以买入，权重为 $-w_{i}$ ，状态变为手中有货
• 起始状态（入口）：手中无货的第 $\geq 2$ 天，因为起始可以买入
• 结束状态（出口）：手中无货的第 $1$ 天或第 $\geq 2$ 天

闫氏DP分析法之状态机分析法

• 状态表示 f[i, 0] f[i, 1] f[i, 2] ：只考虑前 $i$ 天
  • f[i, 0] ：第 $i$ 天手中有货
  • f[i, 1] ：第 $i$ 天手中无货而第 $i - 1$ 天刚卖出
  • f[i, 2] ：第 $i$ 天手中无货且可以买入
• 状态计算
  • f[i, 0] = max(f[i - 1, 0], f[i - 1, 2] - w[i])
  • f[i, 1] = f[i - 1, 0] + w[i]
  • f[i, 2] = max(f[i - 1, 2], f[i - 1, 1])
• 初始化：入口初始为 $0$ ，其他初始化为无穷（由于程序是线性递推，因此只用将 f[0, 0] = f[0, 1] = -INF 即可）

1058代码

AcWing 1052. 设计密码

AcWing 831. KMP字符串

结合KMP的过程。在字符串匹配时，匹配子串上有一个 $j$ 指针，每次判断 s[i] == p[j + 1] ，如果不等，$j$ 就会按照 next[j] 跳转直到相等或跳到开头。我们把跳转看作状态的变化，子串上的每一位字符都是一种状态，则状态机中有 $m + 1$ 种状态（ $m$ 为匹配子串长度，子串头部也算一种状态）。对于每一状态，状态转移的情况取决于当前要匹配的字符 s[i] 。本题而言，被匹配字符串就是我们要设计的密码，匹配子串就是要求不被密码包含的字符串 $T$ 。设计密码是，每一位字符 s[i] 可以有 $26$ 个字母的选择，每个选择会导致匹配子串中状态的一个转移，因此在状态机中有 $m + 1$ 种状态，每个状态有 $26$ 个转移情况（转移情况可能存在重合）

闫氏DP分析法之状态机分析法

• 状态表示 f[i, j] ：已经考虑完密码的前 $i$ 个字符，且匹配子串指针跳到第 $j$ 个字符（状态）的所有方案
• 状态计算：这里的计算和上面几道题的计算有所差别。上面几道题是考虑某一状态是从哪些状态转移过来的；本题是考虑枚举到的状态会转移到哪些状态上去，把本状态的属性叠加到转移到的状态属性上去。
  • $j$ 能转移到 $u$ ：f[i + 1, u] += f[i, j]
• 初始化：f[0][0] = 1

1052代码