笔记汇总
P1
把 $1-n$ 的链提出来然后分类一下就迎刃而解了。

题目要求添加新边后使得最短路最长,我们容易想到新加的边会造成影响,因此必须使得新的路径尽量的长。如果够长的话,最短路径肯定就是原路径了。
有一个细节,如果两个点相邻,只有它们中有一个有其它子树才能计入答案,
所以我们用单调栈去搜的时候,要先跳掉相邻结点,然后单独判断。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 5e5, INF = -1e18;
int n, m, ans, tag;
int s[N], f[N], dist[N], val[N], lit[N], top;
int h[N], e[N], ne[N], w[N], idx;
int q[N], tt;
bool vis[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs1(int u, int father)
{
s[u] = 1;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father || vis[j]) continue;
dfs1(j, u);
s[u] += s[j];
f[u] = max(f[u], f[j] + w[i]);
}
}
bool dfs2(int u, int father)
{
if (u == n) return true;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
vis[j] = true;
lit[ ++ top] = j;
val[top] = w[i];
if (dfs2(j, u)) return true;
top --; vis[j] = false;
}
return false;
}
signed main()
{
memset(h, -1, sizeof h);
scanf("%lld%lld", &n, &m);
for (int i = 1; i < n; i ++ )
{
int a, b, c;
scanf("%lld%lld%lld", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
lit[ ++ top] = 1, vis[1] = true;
dfs2(1, -1); // 找链
for (int i = 1; i <= top; i ++ ) dist[i] = dist[i-1] + val[i]; // 只算链上的
for (int i = 1; i <= top; i ++ ) // 抛掉链之后求子树大小和深度
{
dfs1(lit[i], -1); // 这里可以不维护可以两个子树的情况
tag |= (s[lit[i]] > 2);
}
if (!tag)
{
if (s[lit[1]] > 1 || s[lit[2]] > 1) ans = max(ans, f[lit[1]] + f[lit[2]] + dist[top] - dist[2]);
q[ ++ tt] = 1;
for (int i = 3; i <= top; i ++ )
{
ans = max(ans, f[lit[i]] + f[lit[q[1]]] + dist[q[1]] + dist[top] - dist[i]);
if (s[lit[i]] > 1 || s[lit[i-1]] > 1) ans = max(ans, f[lit[i]] + f[lit[i-1]] + dist[i-1] + dist[top] - dist[i]);
while (tt && f[lit[i-1]] + dist[i-1] >= f[lit[q[tt]]] + dist[q[tt]]) tt --;
q[ ++ tt] = i-1;
}
}
for (int i = 1; i <= m; i ++ )
{
int x;
scanf("%lld", &x);
printf("%lld\n", tag ? dist[top] : min(dist[top], ans + x));
}
}
P2
题目描述十分冗长,实际上就是给你一棵树,问你最少增加多少次边权,使得所有叶子节点到根节点距离相等
有一个十分显然的结论:最后的距离为不增加边权的最大距离。
反证法可证不满足则有更短的距离。
源点不是$1$,是$S$,我们先统计所有叶子与$maxn$值的差,然后再在它们的父节点上减去重合的部分。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10;
int n, S, maxn, ans;
int dist[N], f[N];
int h[N], e[N], ne[N], w[N], idx;
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs1(int u, int father)
{
int cnt = 0; // 儿子数
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
dist[j] = dist[u] + w[i];
cnt ++;
dfs1(j, u);
}
if (!cnt) maxn = max(maxn, dist[u]);
}
void dfs2(int u, int father)
{
int cnt = 0, minn = 1e18;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
cnt ++;
dfs2(j, u);
minn = min(minn, f[j]);
}
if (!cnt)
{
f[u] = maxn - dist[u];
ans += maxn - dist[u];
return;
}
ans -= (cnt - 1) * minn;
f[u] = minn;
}
signed main()
{
memset(h, -1, sizeof h);
scanf("%lld%lld", &n, &S);
for (int i = 1; i < n; i ++ )
{
int a, b, t;
scanf("%lld%lld%lld", &a, &b, &t);
add(a, b, t), add(b, a, t);
}
dfs1(S, -1);
dfs2(S, -1);
printf("%lld", ans);
}
P3
说的是给你一棵树,找出树上的一条链,满足链上结点和该链上子链的数目之和最大。
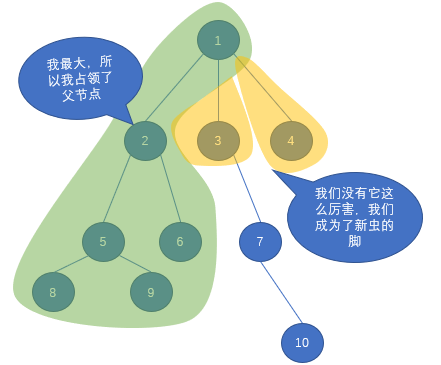
可以发现,这和树的直径很像,我们只要找到最大的子毛毛虫即可,然后再加上其他叶节点的个数。
这样答案有最优子结构性质(由子树中结点数最多的转移),可以用$DP$做。
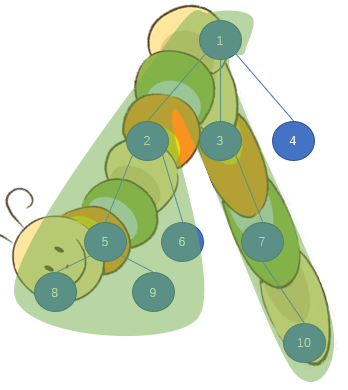
对于横卧在一个结点的毛毛虫,等于由那个结点往下的最大链 $+$ 次大链。
注意,最大链和次大链不能重复,这样就不是一条路径了。
然后我们还需要在最大链中(因为次大链由最大链转移,所以只用统计最大链的)统计一下周边结点(不算父节点,避免转移时重复)
搜索完之后,我们要计算以其它结点为父节点的情况,这是因为答案不一定覆盖根节点。
最后我们还要加上$2$,一个是因为自己,另一个是因为父节点(虽然根没有父节点,但之前我们 少加了一个,所以要加回去)。
特判只有一个结点的情况。
对于这类问题,从小情况考虑,然后考虑不同链(毛毛虫)的竞争,以及向哪里走是最优的。
如果问题有最优子结构性(比如数量),就可以考虑用$DP$求解。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 6e5 + 10;
int n, m;
int f[N][2], d[N], ans;
int h[N], e[N], ne[N], idx;
map<pair<int, int>, int> pc;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int u, int father)
{
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
dfs1(j, u);
if (f[j][0] >= f[u][0])
{
f[u][1] = f[u][0];
f[u][0] = f[j][0];
}
else if (f[j][0] > f[u][1]) f[u][1] = f[j][0];
}
f[u][0] += d[u] - 1;
}
signed main()
{
memset(h, -1, sizeof h);
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= m; i ++ )
{
int a, b;
scanf("%lld%lld", &a, &b);
add(a, b), add(b, a);
if (pc.count({a, b})) continue;
d[a] ++, d[b] ++;
pc[{a, b}] ++;
pc[{b, a}] ++;
}
dfs1(1, -1);
for (int i = 1; i <= n; i ++ )
{
ans = max(ans, f[i][0] + f[i][1] + 2);
}
if (n == 1) ans = 1;
printf("%lld", ans);
}
P4
找环,如果从一个点走到了一个被标记过的点并且这个点不是他的父亲,证明找到环了,然后从这个点一直往上跳到被标记的点,就找到了环,用数组标记即可。
然后选环上的两点,讨论不同拆开方式,跑树形 $DP$ 即可。
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e5+10;
struct edge{//存图
int v,next;
}e[MAXN<<1];
int f[MAXN][2],w[MAXN];//dp数组,点权
double k;
int fa[MAXN];
int head[MAXN<<1],cnt = 0;
int root1,root2;//环上的两个点
int n;
void add(int u,int v){//前向星
e[++cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt;
}
int find(int x){//查找集合
if(fa[x]==x){
return x;
}
else{
return fa[x] = find(fa[x]);
}
}
void circle(int u,int fa){//树形dp
f[u][1] = w[u],f[u][0] = 0;//初始化
for(int i=head[u];i;i=e[i].next){
int v = e[i].v;
if(v!=fa){
circle(v,u);
f[u][0]+=max(f[v][1],f[v][0]);//转移
f[u][1]+=f[v][0];
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&w[i]);
fa[i] = i;//初始化集合
}
for(int i=1;i<=n;i++){
int u,v;
scanf("%d%d",&u,&v);
u++,v++;
if(find(u)==find(v)){//如果在加边前就在一个集合中了,说明找到了环
root1 = u,root2 = v;//记录环上的两个点
continue;//直接跳过加边操作,相当于断开这条边
}
add(u,v);
add(v,u);
fa[find(v)] = find(u);//合并集合
}
scanf("%lf",&k);
circle(root1,0);
double r1 = f[root1][0];//选root1
circle(root2,0);
double r2 = f[root2][0];//选root2
printf("%.1lf",max(r1,r2)*k);//取最大
return 0;
}
P5
/*
我们先找一个重心作为根
然后现在它的所有儿子子树大小都<=n/2
这时候我们考虑一个点u能不能作为答案
要分两种情况讨论
第一种情况是当前根(之前求的重心)的最大子树不包含u
那我们会把这个子树切下来接到u上
也就是我们会判断一下 n - 这个最大子树 - u子树
是否<=n/2
还有一种情况是 最大子树包含了u
这时候有两种可能
一种可能是切掉次大子树
还有一种可能是切最大子树,然后把根连向u
切掉以后把r连向u也是可能的,可能r的其他子树都很小
是切u到r这条路上的某一条边,不一定是和r连的边
*/
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 8e5 + 10;
int n, ans;
int h[N], e[N], ne[N], idx;
int s[N], f1[N], f2[N], p[N], cut[N], mins, root;
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int u, int father)
{
s[u] = 1;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (j == father) continue;
dfs1(j, u);
s[u] += s[j];
if (f1[u] <= s[j])
{
f2[u] = f1[u]; f1[u] = s[j];
}
else if (f2[u] < s[j]) f2[u] = s[j];
}
if (f1[u] <= n >> 1 && n - s[u] <= n >> 1)
root = u;
}
void dfs2(int u, int cnt, int father) // 维护上面的最大子树
{
cut[u] = cnt;
for (int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if (v == father) continue;
if (n - s[u] <= n >> 1) cnt = max(cnt, n-s[u]); // 即节点 u 的祖先中的最大的不超出限制的子树大小
if (f1[u] == s[v]) dfs2(v, max(cnt, f2[u]), u); // 如果父节点最大子树就是自己...
else dfs2(v, max(cnt, f1[u]), u);
}
if (n - s[u] - cut[u] <= n >> 1 || u == root) st[u] = true;
return;
}
signed main()
{
memset(h, -1, sizeof h);
scanf("%lld", &n);
for (int i = 1; i < n; i ++ )
{
int a, b, L;
scanf("%lld%lld", &a, &b);
add(a, b), add(b, a);
}
dfs1(1, -1);
memset(s, 0, sizeof s);
memset(f1, 0, sizeof f1);
memset(f2, 0, sizeof f2);
dfs1(root, -1);
dfs2(root, 0, -1);
for (int i = 1; i <= n; i ++ )
printf(st[i]?"1 ":"0 ");
}

