微积分，是大学的必修，高中也略有涉及，极其简单。

0x00:引入

最开始的时候，牛顿因为在他的论文当中需要计算这样一个面积（我稍稍改变了一下）。

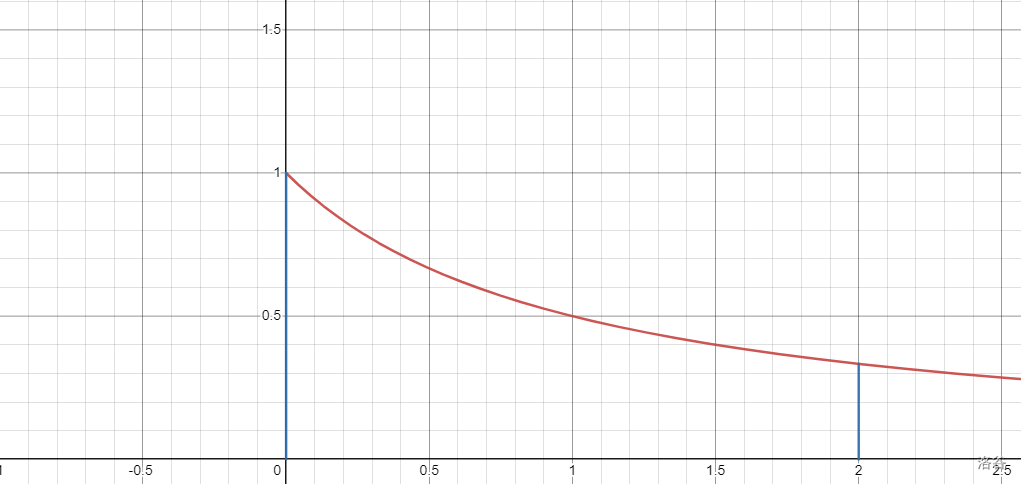
用蓝线，红线（$f(x)=\frac{1}{x+1}$）和$x$轴所围成的就是要求的面积。

牛顿这人啊，脾气不好，不会做题目咋办？自己发明一种数学方法做这道题目！这就是微积分的开端。

0x01:基本函数的导数

一辆车肯定有一个一瞬间的速度，叫做瞬时速度，可以看作极小时间内的路程改变率,可以抽象为以下算式。

$$f’(x)=\frac{f(x+\Delta)-f(x)}{\Delta}$$

如

$$f(x)=x^2$$

则有

$$f’(x)=\frac{f(x+\Delta)-f(x)}{\Delta}=\frac{x^2+2\Delta x + \Delta^2-x^2}{\Delta}=\frac{2\Delta x + \Delta^2}{\Delta}=2x + \Delta=2x$$

所以

$$(x^2)’=2x$$

由此，我们可以导出一些公式

$$h(x)=k\times f(x) \to h’(x)=k \times f’(x)$$

证明：
$h(x)=k \times f(x) \to h’(x)=\frac{k\times f(x+\Delta)-k \times f(x)}{\Delta}=k \times \frac{f(x+\Delta)-f(x)}{\Delta}=k \times f’(x)$

$$f(x)=x^n \to f’(x)=n \times x^{n-1}$$

证明（展开后省略一阶以上无穷小）：
$h(x)=x^n \to h’(x)=\frac{(x+\Delta)^n-x^n}{\Delta} \sim \frac{x^n+n \times \Delta x^{n-1} -x^n}{\Delta} = n \times x^{n-1}$

$$h(x)=f(x)+g(x) \to h’(x)=f’(x)+g’(x)$$

证明：
$h(x)=f(x)+g(x) \to h’(x)=\frac{f(x+\Delta)-f(x)+g(x+\Delta)-g(x)}{\Delta}=\frac{f(x+\Delta)-f(x)}{\Delta}+\frac{g(x+\Delta)-g(x)}{\Delta}=f’(x)+g’(x)$

$$h(x)=f(x)-g(x) \to h’(x)=f’(x)-g’(x)$$

证明：
$h(x)=f(x)-g(x) \to h’(x)=\frac{f(x+\Delta)-f(x)-g(x+\Delta)+g(x)}{\Delta}=\frac{f(x+\Delta)-f(x)}{\Delta}-\frac{g(x+\Delta)-g(x)}{\Delta}=f’(x)-g’(x)$

$$h(x)=f(x)\times g(x) \to h’(x)=f’(x)g(x)+f(x)g’(x)$$

证明：
$h’(x)=\frac{f(x+\Delta)g(x+\Delta)-f(x)g(x)}{\Delta}=\frac{f(x+\Delta)g(x+\Delta)+f(x)g(x+\Delta)-f(x)g(x+\Delta)-f(x)g(x)}{\Delta}=\frac{g(x+\Delta)(f(x+\Delta)-f(x))+f(x)(g(x+\Delta)-g(x))}{\Delta}=g(x)f’(x)+f(x)g’(x)$

均可通过上方的$f’(x)=\frac{f(x+\Delta)-f(x)}{\Delta}$求出。

证明：$h(x)=k \times f(x) \to h’(x)=\frac{k\times f(x+\Delta)-k \times f(x)}{\Delta}=k \times \frac{f(x+\Delta)-f(x)}{\Delta}=k \times f’(x)$

0x02:近似一次函数

如图$f(x)$的导函数$f’(x)$其实是在某一点$f(x)$的切线的斜率。

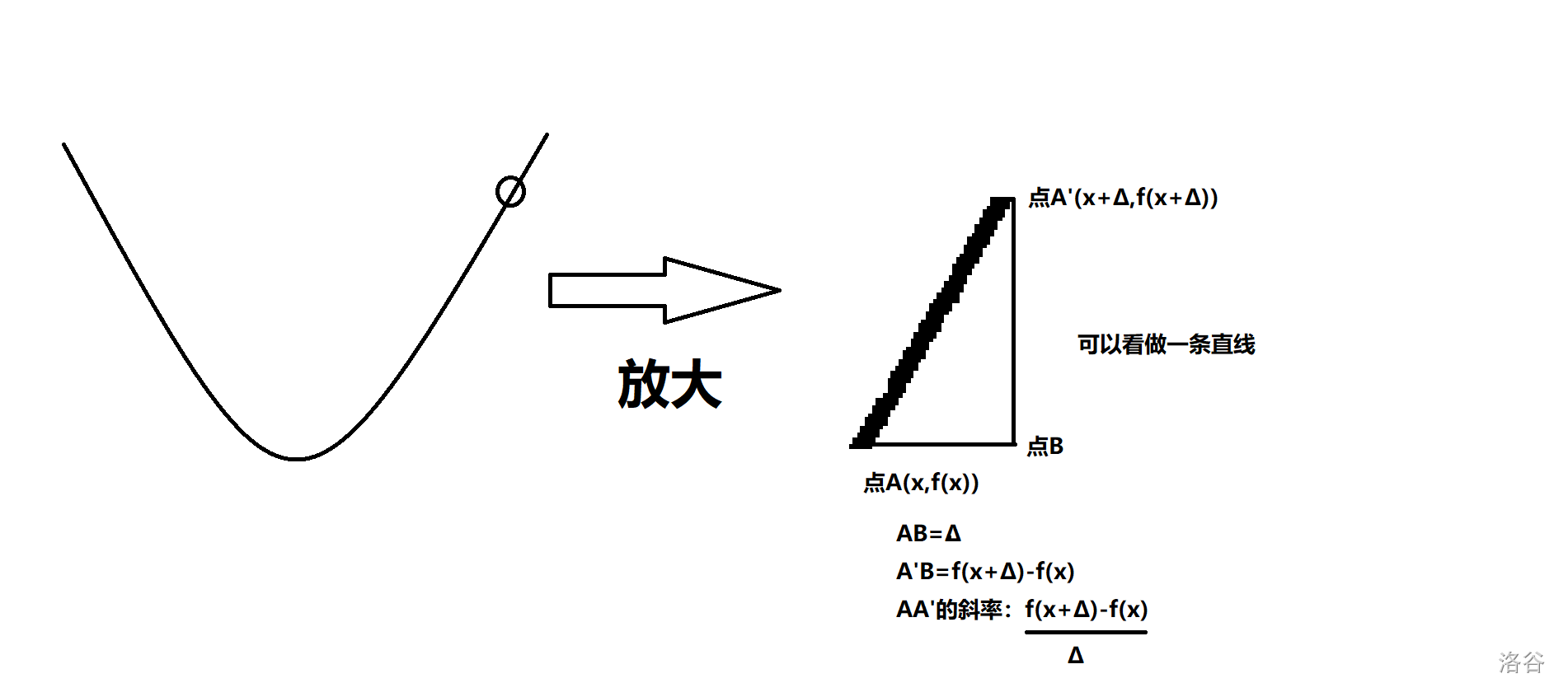
上面的是直接代公式，小学生都会。

如果你想要玩转$desmos$,必须学会近似一次函数。

在$x=a$处,$f(x) \sim f’(a)(x-a)+f(a)$

这就是近似一次函数。

由此可以导出

$$h(x)=\frac{g(x)}{f(x)} \to h’(x)=\frac{g’(x)f(x)-g(x)f’(x)}{f(x)^2}$$

$$h(x)=g(f(x)) \to h’(x)=g’(f(x))f’(x)$$

除法的微分公式我证明一下，复合函数微分公式的证明就是这一章节的作业，想要交作业的在acwing我的任何一个帖子回复证明。

设$p(x)f(x)=1$，则有在$x=a$处,$f(x) \sim f’(a)(x-a)+f(a),p(x) \sim p’(a)(x-a)+p(a)$

所以，$1=f(x)p(x) \sim (f’(a)(x-a)+f(a)) \times (p’(a)(x-a)+p(a)) = (x-a)(p(a)f’(a)+f(a)p’(a)) \sim p(a)f’(a)+f(a)p’(a)$

易得，$p’(a)=\large-\frac{f’(a)}{f(a)^2}$

代入$h’(x)=g’(x)p(x)+g(x)p’(x)$，易得$h’(x)=\frac{g’(x)f(x)-g(x)f’(x)}{f(x)^2}$

0x03:定积分

一个分段函数与x轴与y轴的面积可以通过分割成一个一个的长方形来计算面积。

一个平滑曲线与x轴与y轴的面积也可以通过分割成一个一个的长方形来计算面积。

如(引入部分的图片)：

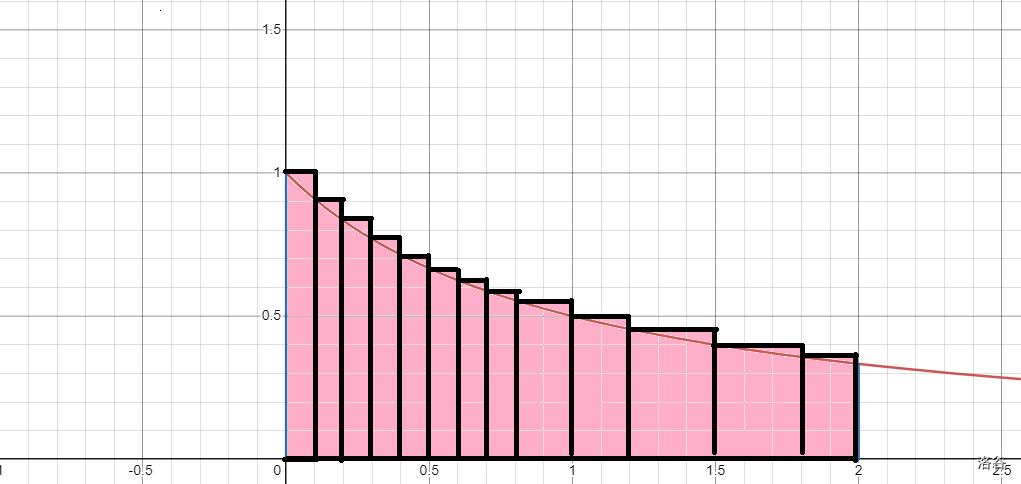
如果粉色的长方形更多，多到多出的部分趋近与0，那么就可以看做真实面积。

这时的面积记作$\int_{0}^{2}\frac{1}{x+1}dx$

若$g’(x)=f(x)$则$\int_{a}^{b}f(x)dx = g(b)-g(a)$

这个就是微积分基本定理。

证明：

设

$$g’(x)=f(x)$$

则

$$g(x_{a+1}-x_{a}) \sim f(x_{a})(x_{a+1}-x_{a})$$

$$g(x_{a+2}-x_{a+1}) \sim f(x_{a+1})(x_{a+2}-x_{a+1})$$

$$g(x_{a+3}-x_{a+2}) \sim f(x_{a+2})(x_{a+3}-x_{a+2})$$

$$g(x_{a+4}-x_{a+3}) \sim f(x_{a+3})(x_{a+4}-x_{a+3})$$

$$g(x_{a+5}-x_{a+4}) \sim f(x_{a+4})(x_{a+5}-x_{a+4})$$

$$g(x_{a+6}-x_{a+5}) \sim f(x_{a+5})(x_{a+6}-x_{a+5})$$

$$\cdots$$

$$g(x_{b}-x_{b-1}) \sim f(x_{b})(x_{b-1}-x_{b})$$

累加:

$$g(x_{b}-x_{a}) \sim f(x_{a})(x_{a+1}-x_{a})+f(x_{a+1})(x_{a+2}-x_{a+1})+\cdots +f(x_{b})(x_{b-1}-x_{b})$$

可以发现，右边的式子就是利用近似一次函数算出来的$\int_{a}^{b}f(x)dx$，所以

若$g’(x)=f(x)$则$\int_{a}^{b}f(x)dx = g(b)-g(a)$

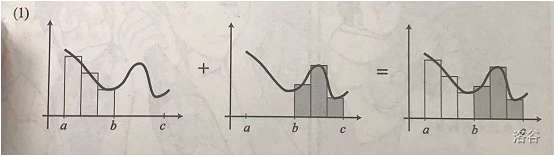
0x04:积分公式

积分公式有3个

$$\int_{a}^{b}f\left(x\right)dx+\int_{b}^{c}f\left(x\right)dx=\int_{a}^{c}f\left(x\right)dx$$

$$\int_{a}^{b}\{f\left(x\right)+g(x)\}dx=\int_{a}^{b}f\left(x\right)dx+\int_{a}^{b}g(x)dx$$

$$\int_{a}^{b}af\left(x\right)dx=a\int_{a}^{b}f\left(x\right)dx$$

图解证明，一看就懂！

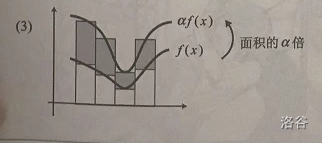
0x05:微分与积分的实例

从万米高空落下的物体几秒落地？（忽略空气阻力，$g=9.8m/s^2$）

这个问题有两种解决方案。

1. 买一架飞机，到万米高空，扔一个东西。

2. 用数学算一算

速度 $v(x)=9.8x$ ，速度的面积 $9.8x\times x \times \frac{1}{2} = 4.9x^2$ ，所以 $x$ 秒间物体落下的距离是 $4.9x^2$

解方程 $10000=4.9x^2$ ，解得 $x$ 约等于 $45.17$

享受45.17秒的痛苦吧——by某恐高症作者

我们教了这么多，是时候来做一些习题了！

1. 函数基本习题

• 已知函数 $f(x)$ 与 $g(x)=8x+10$ ，当 $x$ 趋近于5时，这两个函数误差率趋于0

(1) 求 $f(5)$

趋于5时，这两个函数误差率趋于0，$f(5)=g(5)=50$

(2) 求 $f’(5)$

趋于5时，这两个函数误差率趋于0，$f’(5)=g’(5)=8$

• 已知函数 $f(x)=x^3$ 求 $f’(x)$

$$f’\left(x\right)=\frac{\left(x+\Delta \right)^{3}-x_{3}}{\Delta}=\frac{x^{3}+3\Delta x^{2}+3\Delta \cdot \Delta x+3 \Delta \cdot \Delta \cdot \Delta}{\Delta} = 3x^{2}$$

2.掌握微分的技巧

这里有几个公式大家可以掌握一下

$(x^n)’=n \times x^{n-1}$

$(e^x)’=e^x$

$(a^x)’=a^x \times \ln a$

$(\operatorname{sin}(x))’=\operatorname{cos}(x)$

$(\operatorname{cos}(x))’=-\operatorname{sin}(x)$

快乐解练习(作业)：

求$(x^1+x^1+x^4+x^5+x^1+x^4)’$

求$(2^x)’$

求$(e^{2x}+x^3+x^5+2^x)’$

0x05:三角函数的微分积分证明（未完待续）

先把结论放出来

$(\sin a)’=\cos a$

$(\cos a)’=-\sin a$