笔记汇总
质数
P1
一个合数n必定包含一个小于sqrt(n)的质因子。
上取整技巧:(A+p−1)/p
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
int l, r;
LL v[N], prime[N], n, m;
bool st[N];
LL tot[N], tt;
int main()
{
for (int i = 2; i < N; i ++ )
{
if (v[i] == 0)
{
v[i] = i;
prime[ ++ m] = i;
}
for (int j = 1; j <= m; j ++ )
{
if (prime[j] > v[i] || prime[j] > n / i) break;
v[i * prime[j]] = prime[j];
}
}
while (~scanf("%d%d", &l, &r))
{
tt = 0;
memset(st, false, sizeof st);
n = sqrt(r) + 1;
for (int i = 1; i <= m; i ++ )
{
LL p = prime[i];
for (LL j = max(2*p, (l+p-1)/p*p); j <= r; j += prime[i])
{
st[j-l] = 1;
}
}
for (int i = 0; i <= r-l; i ++ )
if (!st[i] && i + l >= 2)
{
tot[ ++ tt] = l+i;
}
if (tt < 2) puts("There are no adjacent primes.");
else {
int minv = 1, maxv = 1;
for (int i = 1; i < tt; i ++ ) // 因为要+1所以小于
{
int d = tot[i + 1] - tot[i];
if (d > tot[maxv + 1] - tot[maxv]) maxv = i;
if (d < tot[minv + 1] - tot[minv]) minv = i;
}
printf("%lld,%lld are closest, %lld,%lld are most distant.\n",
tot[minv], tot[minv + 1],
tot[maxv], tot[maxv + 1]);
}
}
}
P2
因为 N! 中的质因数,等于 [1,n] 中每个数的质因数的总和,
对于某质因数 p,其倍数都包含这个质因数,则共有 [np] 个,
由此可知 有两个质因子 p 的数,个数为 [np2],用线性筛筛出质数后,累计即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, m;
int p[N], v[N];
inline bool check(int a, int b)
{
return a / b * b == a;
}
void init(int n)
{
// 质数从 2 开始出现
for (int i = 2; i <= n; i ++ )
{
if (!v[i]) p[ ++ m] = i; // 没有被更小的质因子标记过,所以为质数
for (int j = 1; p[j] * i <= n; j ++ ) // 通过质因子标记合数,不能大于上界 n
{
v[i * p[j]] = true; // 标记为合数
if (i % p[j] == 0) break;
// 此时 p[j] 为 i 的一个质因子,也就是存在一个 t,满足 p[j] * t == i
// 因为要求每个合数仅被它的最小素因子筛去正好一次,i 的质因数若小于 p[j],
// 就不满足为最小质因数,所以直接退出
}
}
}
int main()
{
scanf("%d", &n);
init(n);
for (int i = 1; i <= m; i ++ )
{
int s = 0;
for (int j = n; j; j /= p[i]) s += j / p[i];
printf("%d %d\n", p[i], s);
}
return 0;
}
总结
欧拉函数是积性函数,
埃氏筛筛掉质数的倍数来找质数,线性筛筛掉每个数的最小质因数来找质数。
P1
约数互相独立,通过乘法原理计算个数,同时还有pa01的情况。
维护数与约数个数,暴搜即可。
#include <bits/stdc++.h>
using namespace std;
const int primes[9] = {2, 3, 5, 7, 11, 13, 17, 19, 23}; // 最优性剪枝
typedef long long LL;
int n;
int number, cnt;
void dfs(int u, int last, int p, int s)
{
if (s > cnt || (s == cnt && p < number)
{
cnt = s;
number = p;
}
if (u == 9) return;
for (int i = 1; i <= last; i ++ )
{
if ((LL)p * primes[u] > n) return; // 可行性剪枝
p *= primes[u];
dfs(u + 1, i, p, s * (i + 1));
}
}
int main()
{
scanf("%d", &n);
dfs(0, 30, 1, 1);
printf("%d", number);
return 0;
}
P2
式子可以化简成,n∗k−∑ni=1⌊k/i⌋\*i
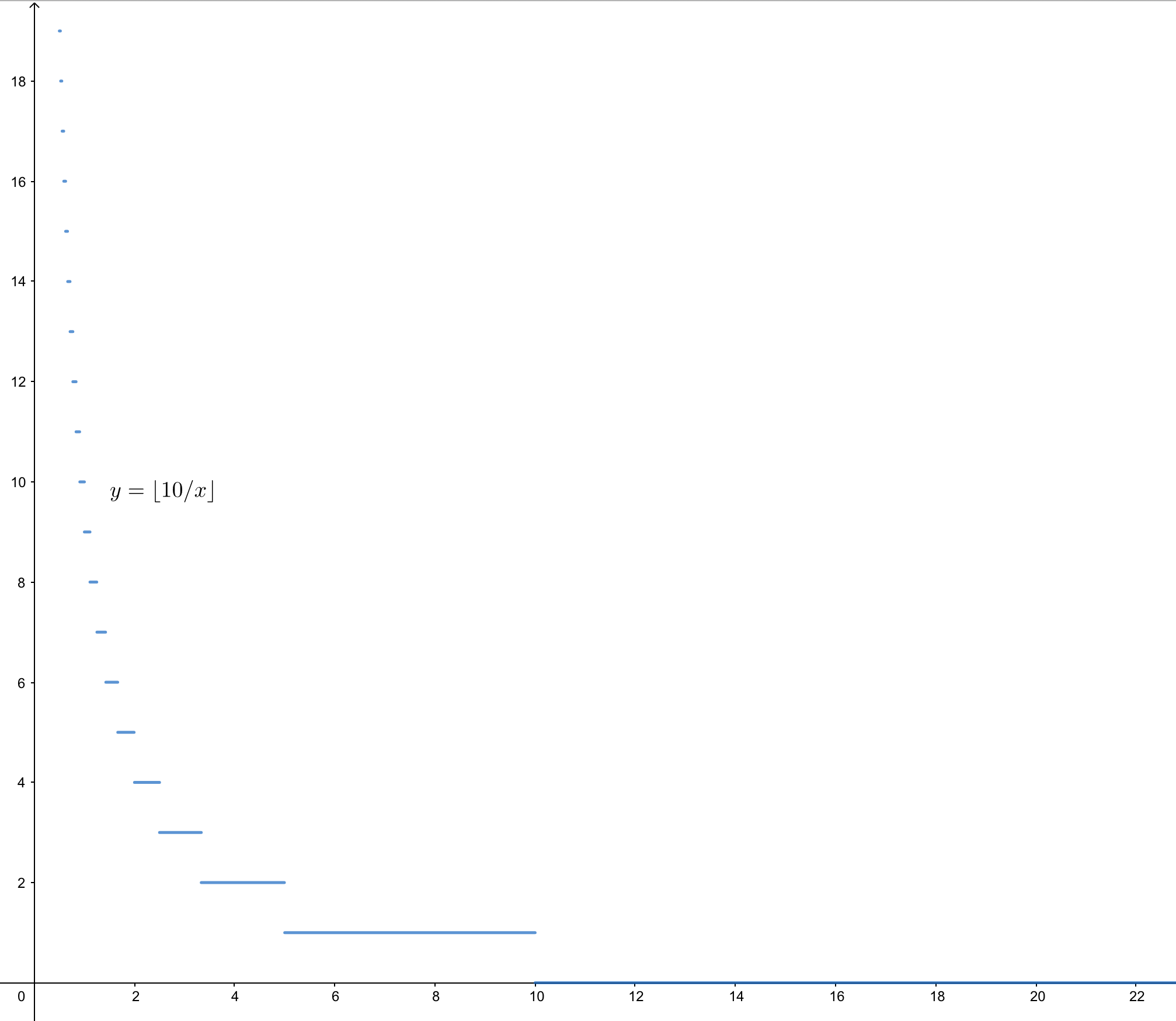
对于形如,∑ni=1⌊n/i⌋ 的式子,
我们可以用整除分块解决。
讨论发现,它的数字是按块状分布的,且可以分成2√n段,
一个整数的约数个数为 2√n
int calc(int n)
{
int res = 0;
for (int l = 1, r; l <= n; l = r + 1) //进入下一块
{
r = n / (n / l); //得到右端点下标
res += (r - l + 1) * (n / l); //(r-l+1)是块长度,(n/l)是这个块的数字
}
return res;
}
回到本题,
对于一个块而言,块中每个数都相同,因此可以记同一个块中的 ⌊k/i⌋=T
可以写成,∑ri=lT∑ri=li
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n, k;
int main()
{
scanf("%lld%lld", &n, &k);
LL ans = n * k;
for (int l = 1, r; l <= n; l = r + 1) // 进入下一块
{
if (k / l == 0) break;
r = min(k / (k / l), n); // 块的右端点
ans -= (r - l + 1) * (k / l) * (l + r) / 2;
}
printf("%lld", ans);
}
P3
因为本题 x,必然是 b1 的约数,所以找到所有约数判断即可。
首先预处理质数,再计算 b1 的所有质因数,用 dfs 找到它的约数,
#include <bits/stdc++.h>
#define p first
#define s second
using namespace std;
const int N = 50010, M = 160;
typedef long long LL;
typedef pair<int, int> PII;
int n, m;
int a, d, b, e;
int dcnt, fcnt;
int p[N], v[N], dvr[N];
PII f[M];
inline bool check(int a, int b) // a%b == 0
{
return a / b * b == a;
}
void init(int n) // 素数预处理
{
for (int i = 2; i <= n; i ++ )
{
if (!v[i]) p[ ++ m] = i;
for (int j = 1; p[j] <= n / i; j ++ )
{
v[i * p[j]] = 1;
if (check(i, p[j])) break;
}
}
}
void dfs(int u, int p)
{
if (u > fcnt)
{
dvr[ ++ dcnt] = p;
return;
}
for (int i = 0; i <= f[u].s; i ++ )
{
dfs(u + 1, p);
p *= f[u].p;
}
}
int gcd(int a, int b)
{
if (!b) return a;
return gcd(b, a % b);
}
int main()
{
init(N - 1);
scanf("%d", &n);
while (n -- )
{
scanf("%d %d %d %d", &a, &d, &b, &e);
fcnt = 0;
int t = e;
for (int i = 1; p[i] <= t / p[i]; i ++ ) // 分解质因数
if (check(t, p[i]))
{
int s = 0;
while (check(t, p[i])) t /= p[i], s ++;
f[ ++ fcnt] = {p[i], s};
}
if (t > 1) f[ ++ fcnt] = {t, 1};
dcnt = 0;
dfs(1, 1); // 枚举约数
int res = 0;
for (int i = 1; i <= dcnt; i ++ )
{
int x = dvr[i];
if (gcd(a, x) == d && (LL)b * x / gcd(b, x) == e) res ++;
// 判断合法解
}
printf("%d\n", res);
}
}
总结
线性筛可以筛出质数,试除法可以得到质因数,dfs 可以枚举素数,
时间复杂度分别为 O(n),O(sqrt(n)),≈10log(n)
化简式子再求值。
找到左右端点,就可以分块计算了。
P1
一个点不可见等于它是之前的点的线性组合,
本题等价于求一段区间的欧拉函数,
这可以在线性筛中得到
φ(N)=N×p1−1p1×p2−1p2×…×pm−1pm
注意的是 1,1 要特判,因为是有序点对所以要乘2
为1的情况也要特殊计算。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int T, n, m;
int v[N], phi[N], p[N];
int s[N];
bool check(int a, int b)
{
return a / b * b == a;
}
void init(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; i ++ )
{
if (!v[i])
{
p[ ++ m] = i;
phi[i] = i - 1;
}
for (int j = 1; p[j] <= n / i; j ++ )
{
v[i * p[j]] = 1;
if (check(i, p[j]))
{
phi[i * p[j]] = phi[i] * p[j];
break;
}
phi[i * p[j]] = phi[i] * (p[j] - 1);
}
}
for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + phi[i];
}
int main()
{
init(N - 1);
scanf("%d", &T);
for (int i = 1; i <= T; i ++ )
{
scanf("%d", &n);
printf("%d %d %d\n", i, n, s[n] * 2 + 1);
}
return 0;
}
P2
先化简,888=8∗111=8∗103−1/9
这个的目的是为了快速计算8组成的数字。
L 很大,我们不能直接去凑,再次分析式子,
化简后可知,9L|8∗(10x−1)
计算最小的 x,所以继续移没有未知数的项,9/8L|10x−1
看到整除符号,我们可以等价化为同余符号,10x≡1(mod9/8L),
对于 ax≡b(modm)(gcd(a,m)=1) 有解,但这不一定是最小解,
所以我们还要在最后化简。
由于 9/8L 不一定是整数,我们可以等价变形为 9/dL(gcd(L,8)==d),
注意这之后还要判一下是否与 10 互质。
本题思路:暴力枚举φ(c)的所有约数,找出满足条件的最小整数 x。
这需要用 快速幂 + 龟速乘
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL l;
LL gcd(LL a, LL b)
{
if (!b) return a;
return gcd(b, a % b);
}
LL get_euler(LL c)
{
LL res = c;
for (int i = 2; i <= c / i; i ++ )
if (c / i * i == c)
{
int s = 0;
while (c / i * i == c) ++ s, c /= i;
res = res / i * (i-1);
}
if (c > 1) res = res / c * (c-1);
return res;
}
//龟速乘
LL qmul(LL a, LL b, LL c) {
LL res = 0;
while (b) {
if (b & 1) res = (res + a) % c;
a = (a + a) % c;
b >>= 1;
}
return res;
}
//快速幂
LL qmi(LL a, LL b, LL c) {
LL res = 1;
while (b) {
if (b & 1) res = qmul(res, a, c);
a = qmul(a, a, c);
b >>= 1;
}
return res;
}
int main()
{
LL T = 1;
while (scanf("%lld", &l), l)
{
int d = gcd(l, 8);
LL c = l * 9 / d;
LL phi = get_euler(c);
LL res = 1e17;
if (c % 2 == 0 || c % 5 == 0) res = 0;
else {
for (LL i = 1; i <= phi / i; i ++ )
{
if (phi % i == 0)
{
if (qmi(10, i, c) == 1) res = min(res, i);
if (qmi(10, phi/i, c) == 1) res = min(res, phi/i);
}
}
}
printf("Case %d: %lld\n", T ++ , res);
}
return 0;
}
P3
ax≡b(modm),可以变形为 ax+my=b
此方程有解当且仅当 gcd(a,m)|b,
本题中有解,仅当 gcd(a,m)|1eitherisgcd(a,m)=1
可以用拓展欧几里得算法求解,同样它的所有线性组合 x0+b/gcd(a,m)都是解。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main()
{
LL a, b, x, y;
scanf("%lld %lld", &a, &b);
exgcd(a, b, x, y);
printf("%lld", (x % b + b) % b);
}
P4
由小到大合并,我们可以将没有未知数的两式合并为没有未知数的一式,
所以正确,链接崩溃了
k1=inv(m1/d,m2/d)∗(c2−c1)/d+y(m2/d)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
LL d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
LL gcd(LL a, LL b)
{
if (!b) return a;
return gcd(b, a % b);
}
LL lcm(LL a, LL b)
{
return a * b / gcd(a, b);
}
LL inv(LL a, LL mod)
{
LL x, y;
exgcd(a, mod, x, y);
return (x % mod + mod) % mod;
}
int n;
int main()
{
LL a1, m1;
scanf("%d", &n);
scanf("%lld%lld", &a1, &m1); // a1 + m1k1 = a2 + m2k2
for (int i = 1; i < n; i ++ )
{
LL a2, m2, k1, k2;
scanf("%lld%lld", &a2, &m2);
LL d = exgcd(a1, a2, k1, k2); // 求两方程的解
if ((m2 - m1) % d) // 无解,a2 - a1 = m1k1 - m2k2,d不整除的话无法线性表示
{
puts("-1");
return 0;
}
// 过程量可能会爆longlong
m1 = inv(a1/d, a2/d) * (m2 - m1) / d % (a2 / d) * a1 + m1;
a1 = lcm(a1, a2);
m1 = (m1 % a1 + a1) % a1;
}
printf("%lld", m1);
}

