基环树
概念:就是在树上再加一条边使之存在环,就称为基环树
内向基环树:
有向图,类似基环树的结构,但每个点有且仅有一条出边,即k个点有k条边,那么必然是存在环的(且只有一个),其它点均指向这个环,如下:
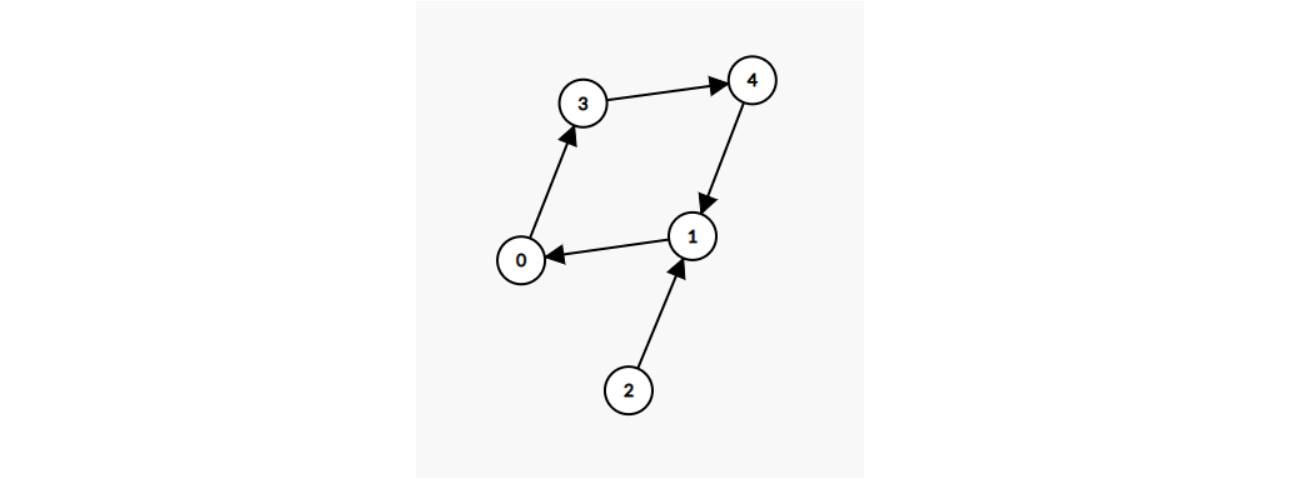
注意基环也可能仅包含两个点,在某些题中这个性质会让题目有很大改变
通用的拓扑解题方法
Eg1: leetcode.6135
一、拓扑排序后维护最大值O(n)
本题要求的是图中最长环,由每个结点最多只有一个出边可知这是一个内向基环树森林(存在多个含环有向图连通块),那么我们就可以先拓扑排序将所有环分离出来,然后再枚举所有环维护最大值
// 注意每次取edges的时候都要判断非-1
class Solution {
public:
int longestCycle(vector<int>& edges) {
int n = edges.size();
vector<int> d(n);
for (int i = 0; i < n; i ++){
if (edges[i] == -1) continue;
d[edges[i]] ++; // 统计每个点的入度
}
queue<int> q;
for (int i = 0; i < n; i ++) // 将叶结点初始化进q
if (!d[i]) q.emplace(i);
while (q.size()) // 用叶结点做拓扑排序,将挂在基树环上的点都标记入度为0
{
auto t = q.front();
q.pop();
int w = edges[t];
if (w != -1 && -- d[w] == 0) q.emplace(w);
}
int ans = -1;
for (int i = 0; i < n; i ++)
{
if (d[i] <= 0) continue;
int ring_size = 1;
for (int j = edges[i]; j != i && j != -1; j = edges[j])
{
d[j] = -1;
ring_size ++;
}
ans = max(ans, ring_size);
}
return ans;
}
};
二、枚举所有点,如果这个点还没有被访问,就判断它是否能形成环O(n)
每次从没有访问过的点找环的时候要记录开始时间戳,为了避免将下面的情况识别为环:
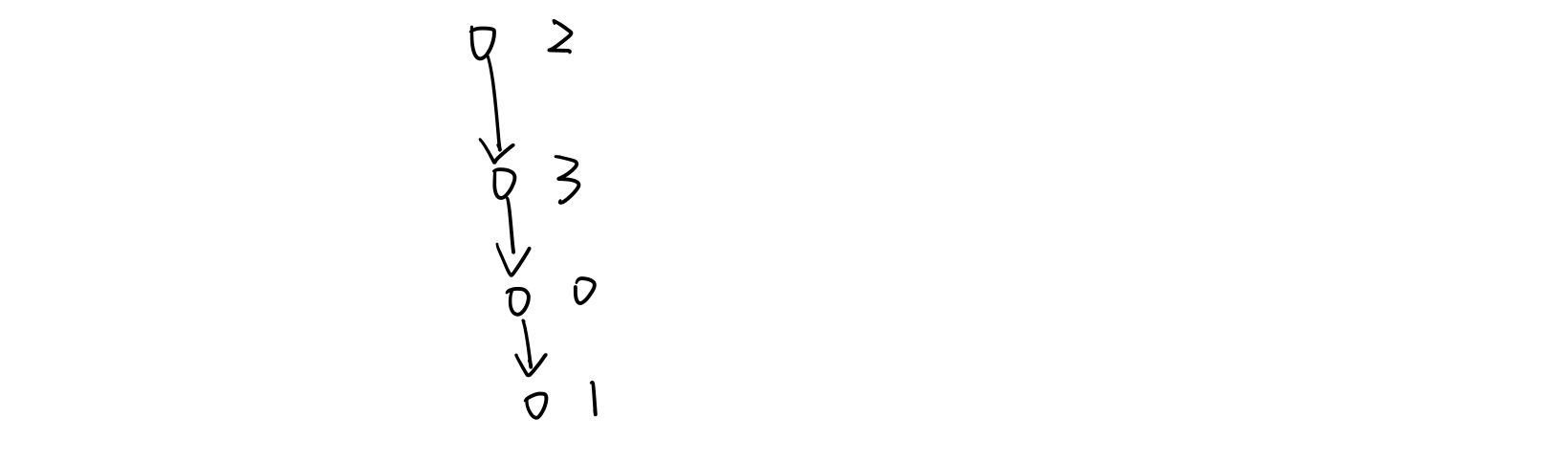
class Solution {
public:
int longestCycle(vector<int>& edges) {
int n = edges.size(), time[n], ans = -1;
memset(time, 0, sizeof time);
for (int i = 0, timedelta = 1; i < n; i ++)
{
if (time[i]) continue; // 如果这个点已经被访问过
for (int t = i, start_time = timedelta; t != -1; t = edges[t]) // 判断当前点是否能形成环
{
if (time[t])
{
if (time[t] >= start_time) ans = max(ans, timedelta - time[t]);
break;
}
time[t] = timedelta ++;
}
}
return ans;
}
};
Eg2: leetcode.6135
要求最多能安排到一张桌子上的人员个数,这里就要分别讨论长度为2的基环和长度大于2的基环了
①如果基环长度大于2
那么就不能再将链安排进圆桌,因为会破坏链上原有的友好关系
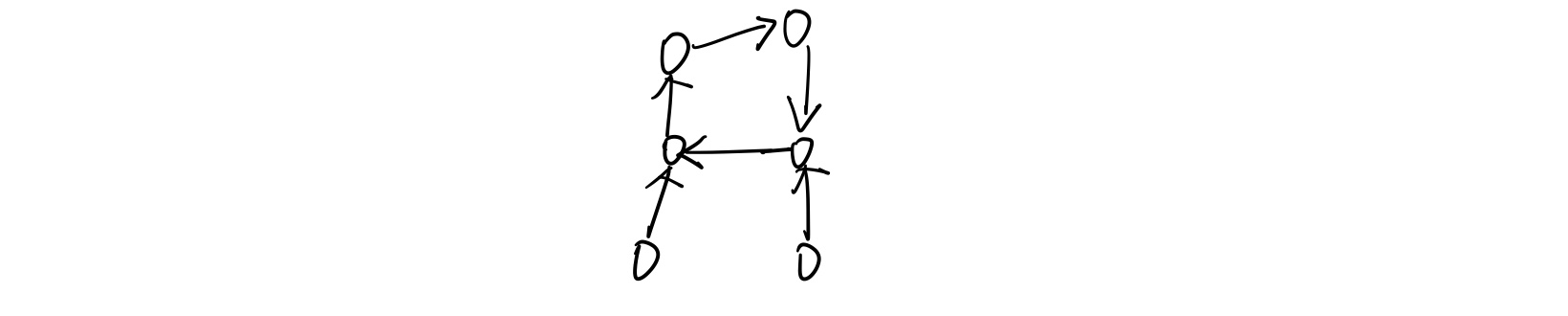
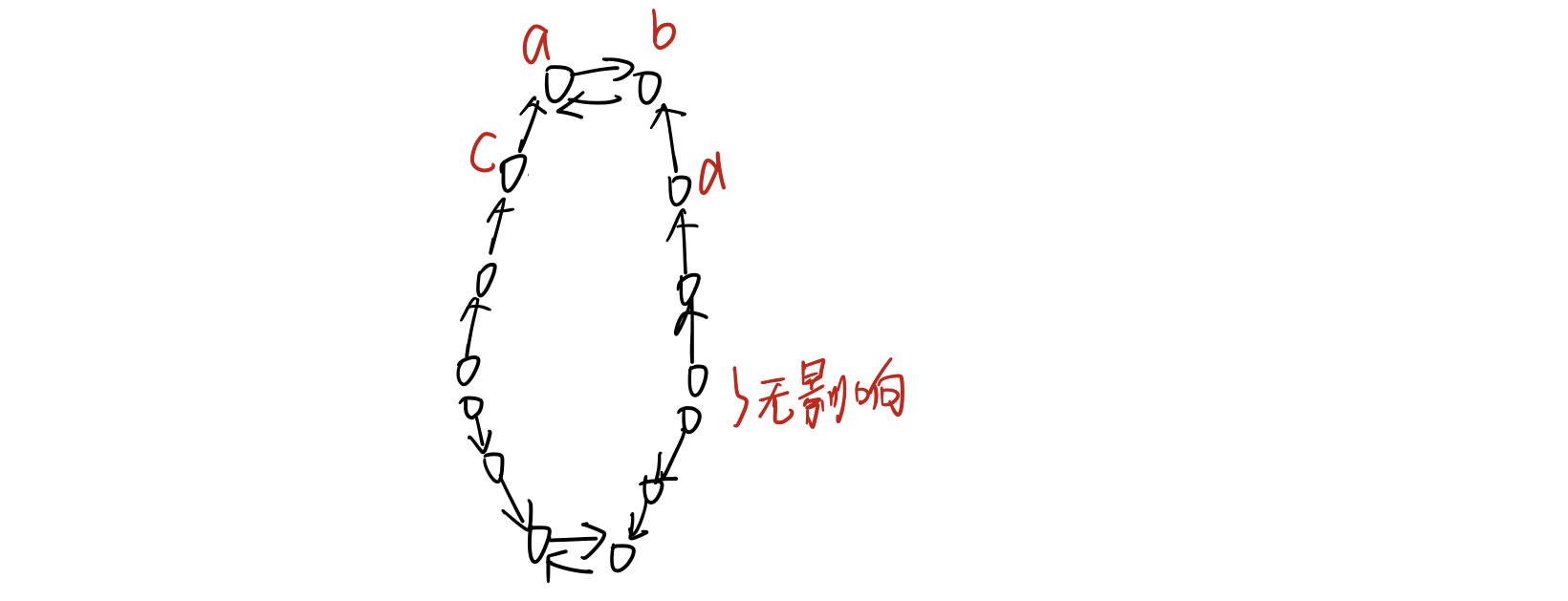
②如果基环长度为2
那么可以将两个点相连的链都挂上,且不破坏原有的友好关系,并且还可以安排多个这种形式的友好关系到一张桌子
class Solution {
public:
int maximumInvitations(vector<int>& g) {
int n = g.size();
int d[n]; memset(d, 0, sizeof d);
for (auto t : g) d[t] ++;
int max_depth[n]; memset(max_depth, 0, sizeof max_depth);
queue<int> q;
for (int i = 0; i < n; i ++)
if (!d[i]) q.emplace(i);
while (q.size()) // 拓扑去链留环
{
auto t = q.front();
q.pop();
int ne = g[t];
if (ne == -1) continue;
max_depth[ne] = max(max_depth[ne], max_depth[t] + 1);
if (-- d[ne] == 0) q.emplace(ne);
}
int max_type1 = -1, max_type2 = 0;
for (int i = 0; i < n; i ++)
{
if (d[i] == 0) continue;
int ring_len = 1;
for (int j = g[i]; j != i; j = g[j])
{
d[j] = 0;
ring_len ++;
}
// 因为可以安排多个奇数环长度为2的到一张桌子,因此max_type2是累加
if (ring_len == 2) max_type2 += 2 + max_depth[i] + max_depth[g[i]];
else max_type1 = max(max_type1, ring_len);
}
return max(max_type1, max_type2);
}
};

