Part1 准备工作(已于2022/7/30日更新,有兴趣的朋友可以看看:文章)

Part 2 BST的检索与插入(2022/7/31日更新)

Part 3 BST的前驱/后继 会在(2022/8/1日更新) 有难度 敬请期待

非常easy

第三部分 BST的检索

在$BST$中查找$val$,设当前遍历的树(子树)的根节点为$p$

1. 当节点$p$的数字$num$等于$val$,则查找成功.

2. 当节点$p$的数字$num$小于$val$,则分情况讨论

2. 1. $p$存在左子树,则遍历左子树

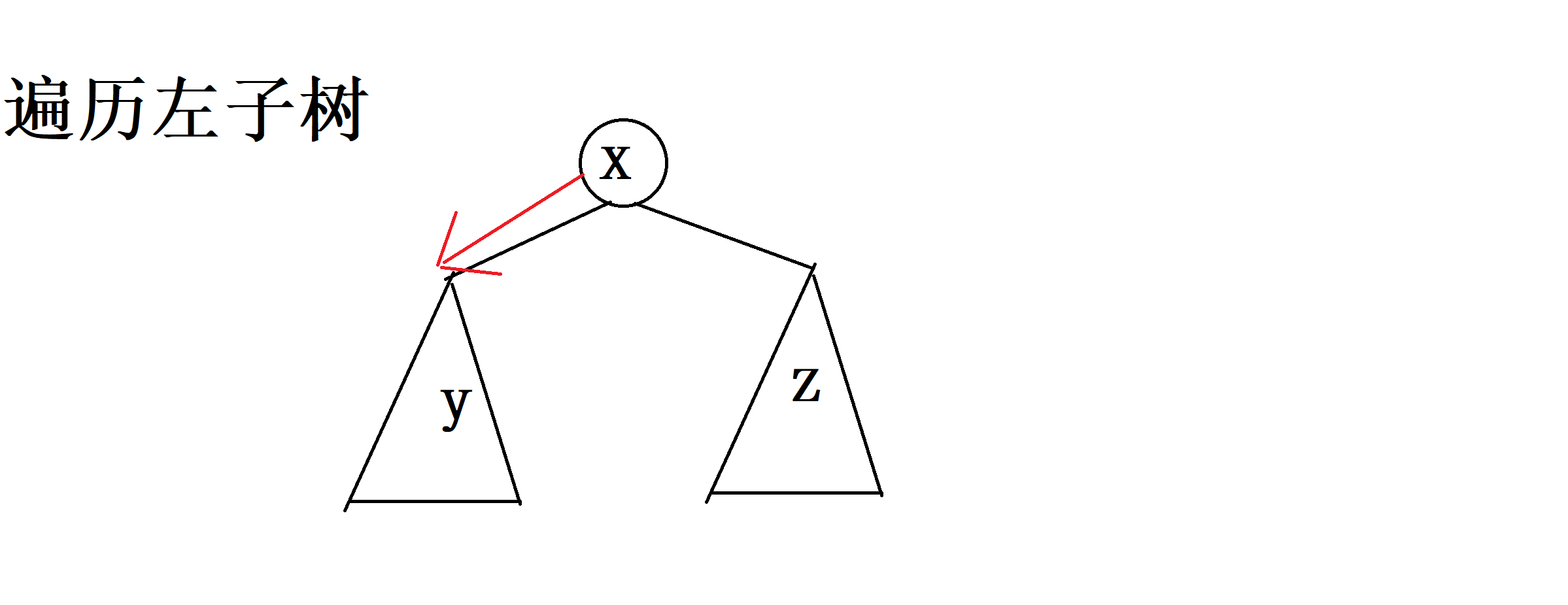
2. 2. $p$不存在左子树,那就找不到了qwq

3. 当节点$p$的数字$num$大于$val$,也分情况讨论

2. 1. $p$存在右子树,则遍历右子树

2. 2. $p$不存在右子树,那就找不到了qwq × 2

代码(非常简短)

int Get(int p,int val)
{
    if(p==0)return 0;                           //由父节点引导到了这里,却发现父节点根本没这个儿子,失败qwq
    if(val==a[p].val)return p;                  //找到了!!!
    if(val<a[p].val)                            //val比a[p].val小,遍历左子树
    {
        return Get(a[p].l,val);
    }
    else                                        //val比a[p].val大,遍历右子树
    {
        return Get(a[p].r,val);
    }
}

第四部分 BST的插入

与查询类似

假如插入的节点的数据为$val$,假设当前没有这个数值

$p$被引导到了$val$应该存入的位置

却发现这里根本没有节点

废话,那不就是为它留的吗

在该位置新建一个节点即可

代码(同样很简短)

void Insert(int& p,int val)             //注意p是引用,当p修改时,其父节点的l或r也会跟着被修改（因为是由父节点调用的）
{
    if(p==0)                            //该处不存在节点
    {
        p=New(val);                     //不清楚New的看前面一篇文章
        return;
    }
    if(a[p].val==val)return;            //有一个相同数值已经提前占了位置,那就插入失败
    if(val<a[p].val)Insert(a[p].l,val); //在左子节点做处理
    else Insert(a[p].r,val);            //在右子节点做处理
}