前置知识

向量叉积，两个向量的形式，这里的 $PII$ 为一个向量

#define PII pair<int, int>
#define x first
#define y second
int cross(PII A, PII B) {// vector(A) * vector(B)
    return A.x * B.y - B.x * A.y;
}

三个点的形式，$OA$向量 叉乘 $OB$向量，这里 $PII$ 为点

#define PII pair<int, int>
#define x first
#define y second
int area(PII o, PII a, PII b) {// vector(OA) * vector(OB)
    PII A = {a.x - o.x, a.y - o.y};
    PII B = {b.x - o.x, b.y - o.y};
    return cross(A, B);
}

A

以最小 $y$ 的点为原点，用叉积进行排序，保证相邻两个点的叉积 $>0$，中间那个点和原点的连线就是题目需要的

#include <bits/stdc++.h>

using namespace std;
#define int long long
#define rep(i, l, r) for(int i = l; i <= (int)r; i ++)
#define PII pair<int, int>
const int N = 2e5 + 5;
#define x first
#define y second

int n;
struct Point {
    PII p;
    int id; 
} o[N];
int cross(PII A, PII B) {// vector(A) * vector(B)
    return A.x * B.y - B.x * A.y;
}
int area(PII o, PII a, PII b) {// vector(OA) * vector(OB)
    PII A = {a.x - o.x, a.y - o.y};
    PII B = {b.x - o.x, b.y - o.y};
    return cross(A, B);
}
void solve() {
    cin >> n;
    if(n & 1) {
        cout << "-1 -1\n";
    } else {
        int miny = 1e9, minid;
        rep(i, 1, n) {
            int x, y;
            cin >> x >> y;
            o[i] = {{x, y}, i};
            if(y < miny) miny = y, minid = i;
        }
        swap(o[1], o[minid]);
        sort(o + 2, o + 1 + n, [&] (Point &A, Point &B) {
            return area(o[1].p, A.p, B.p) > 0;
        });
        cout << o[1].id << " " << o[n / 2 + 1].id << '\n';
    }   
}
main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int _ = 1;
    // cin >> _;
    while(_ --) {
        solve();
    }
    return 0;
}

B

让点按这个顺序输出

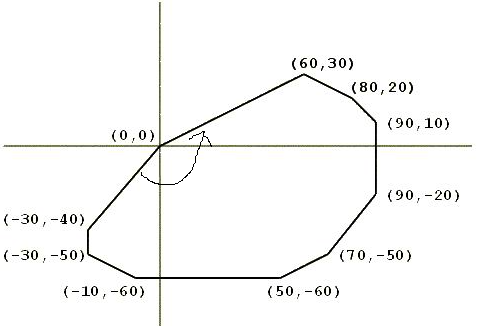
连接原点和各点，就是让相邻的向量叉积 $>0$

#include <iostream>
#include <algorithm>

using namespace std;
#define int long long
#define rep(i, l, r) for(int i = l; i <= (int)r; i ++)
#define PII pair<int, int>
const int N = 2e5 + 5;
#define x first
#define y second

int n = 1;
PII o[N];
int cross(PII A, PII B) {// vector(A) * vector(B)
    return A.x * B.y - B.x * A.y;
}
int area(PII o, PII a, PII b) {// vector(OA) * vector(OB)
    // PII A = {a.x - o.x, a.y - o.y};
    // PII B = {b.x - o.x, b.y - o.y};
    PII A, B;
    A.x = a.x - o.x, A.y = a.y - o.y;
    B.x = b.x - o.x, B.y = b.y - o.y;
    return cross(A, B);
}
bool cmp(PII A, PII B) {
    return area(o[1], A, B) > 0;
}
void solve() {
    while(cin >> o[n].x >> o[n].y) n ++;
    n --;
    sort(o + 2, o + 1 + n, cmp);
    for(int i = 1; i <= n; i ++) {
        cout << "(";
        cout << o[i].x << "," << o[i].y;
        cout << ")\n";
    }
}
main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int _ = 1;
    // cin >> _;
    while(_ --) {
        solve();
    }
    return 0;
}

C

点在三角形内，等价这三对向量叉乘的符号相同，在线上用两点距离判断

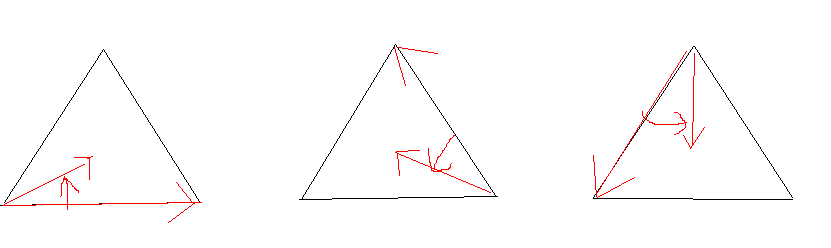
#include <bits/stdc++.h>

using namespace std;

#define rep(i, l, r) for(int i = l; i <= (int)r; i ++)
#define PII pair<int, int>
const int N = 2e5 + 5;
#define x first
#define y second
const double eps = 1e-5;


int x[N], y[N];
int sign(int x) {
    if(x > 0) return 1;
    if(x < 0) return -1;
    return 0;
}
int cross(PII A, PII B) {// vector(A) * vector(B)
    return A.x * B.y - B.x * A.y;
}
int area(PII o, PII a, PII b) {// vector(OA) * vector(OB)
    PII A = {a.x - o.x, a.y - o.y};
    PII B = {b.x - o.x, b.y - o.y};
    return sign(cross(A, B));
}
double dist(PII A, PII B) {
    int dx = A.x - B.x;
    int dy = A.y - B.y;
    return sqrt(dx * dx + dy * dy);
}
int solve() {
    rep(i, 1, 4) scanf(" (%d,%d)", &x[i], &y[i]);

    // rep(i, 1, 4) cout << x[i] << " " << y[i] << '\n';
    rep(i, 1, 3) if(x[i] == x[4] && y[i] == y[4]) return 4;

    PII C = {x[4], y[4]};
    bool pos = false, neg = false;
    rep(i, 1, 3) {
        int j = i + 1;
        if(j == 4) j = 1;
        PII A = {x[i], y[i]}, B = {x[j], y[j]};
        int t = area(A, B, C);
        if(dist(A, C) + dist(B, C) - dist(A, B) < eps) return 3;
        if(t > 0) pos = true;
        if(t < 0) neg = true;
    }
    if(pos && neg) return 2;
    return 1;
}
main() {
    // ios::sync_with_stdio(false);
    // cin.tie(0); cout.tie(0);
    int _ = 1;
    // cin >> _;
    while(_ --) {
        cout << solve();
    }
    return 0;
}

D

两点确定一条直线，枚举所有直线，另外一个点也在这条线上可以用向量叉积，叉积为$0$说明在同一直线

#include <bits/stdc++.h>

using namespace std;
#define rep(i, l, r) for(int i = l; i <= (int)r; i ++)
#define PII pair<int, int>
const int N = 2e5 + 5;
#define x first
#define y second

int n;
PII p[N];
int cross(PII A, PII B) {// vector(A) * vector(B)
    return A.x * B.y - B.x * A.y;
}
int area(PII o, PII a, PII b) {// vector(OA) * vector(OB)
    PII A = {a.x - o.x, a.y - o.y};
    PII B = {b.x - o.x, b.y - o.y};
    return cross(A, B);
}
void solve() {
    cin >> n;
    rep(i, 1, n) {
        int x, y;
        cin >> x >> y;
        p[i] = {x, y};
    }

    int qwq = 0;
    for(int i = 1; i <= n; i ++) {
        for(int j = i + 1; j <= n; j ++) {
            int cnt = 0;
            PII A = p[i], B = p[j];
            for(int k = 1; k <= n; k ++) {
                if(k == i || k == j) continue;
                PII C = p[k];
                if(area(A, B, C) == 0) cnt ++;
            }
            qwq = max(qwq, cnt + 2);
        }
    }
    cout << qwq << '\n';
}
main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int _ = 1;
    // cin >> _;
    while(_ --) {
        solve();
    }
    return 0;
}

D

每个点都在左侧向量的右侧，右侧向量的左侧，叉乘后符号不同，满足两段性，可以二分

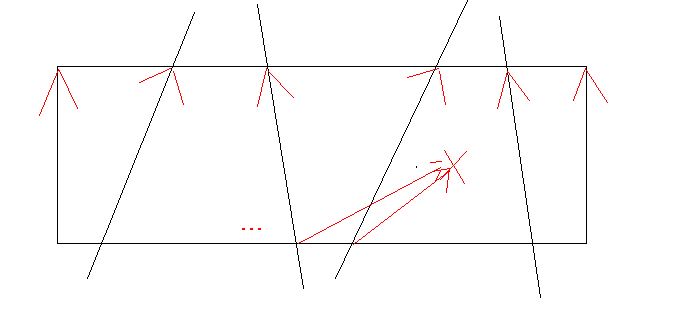
#include <iostream>
#include <cstring>

using namespace std;
#define int long long
#define rep(i, l, r) for(int i = l; i <= (int)r; i ++)
#define PII pair<int, int>
const int N = 2e5 + 5;
#define x first
#define y second

int n, m;
PII up[N], down[N];
int ans[N];
int cross(PII A, PII B) {// A * B
    return A.x * B.y - B.x * A.y;
}
int area(PII o, PII a, PII b) {// OA * OB
    // PII A = {a.x - o.x, a.y - o.y};
    // PII B = {b.x - o.x, b.y - o.y};
    PII A, B;
    A.x = a.x - o.x, A.y = a.y - o.y;
    B.x = b.x - o.x, B.y = b.y - o.y;
    return cross(A, B);
}
bool check(int mid, int x, int y) {
    PII o = down[mid];
    PII a = up[mid];
    // PII b = {x, y};
    PII b;
    b.x = x, b.y = y;
    return area(o, a, b) < 0;
}
int find(int x, int y) {
    int l = 0, r = n;
    while(l < r) {
        int mid = l + r + 1 >> 1;
        if(check(mid, x, y))
            l = mid;
        else
            r = mid - 1;
    }
    return l;
}
void solve() {
    bool is_first = true;
    while(cin >> n && n) {
        int x1, y1, x2, y2;
        cin >> m >> x1 >> y1 >> x2 >> y2;

        // up[0] = {x1, y1}, down[0] = {x1, y2};
        up[0].x = x1, up[0].y = y1;
        down[0].x = x1, down[0].y = y2;
        for(int i = 1; i <= n; i ++) {
            int u, l;
            cin >> u >> l;
            // up[i] = {u, y1};
            // down[i] = {l, y2};
            up[i].x = u, up[i].y = y1;
            down[i].x = l, down[i].y = y2;
        }

        memset(ans, 0, sizeof ans);
        while(m --) {
            int x, y;
            cin >> x >> y;
            ans[find(x, y)] ++;
        }

        if(is_first) is_first = false;
        else cout << '\n';
        for(int i = 0; i <= n; i ++) {
            cout << i << ": ";
            cout << ans[i] << '\n';
        }
    }
}
main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int _ = 1;
    // cin >> _;
    while(_ --) {
        solve();
    }
    return 0;
}

D

如果存在这样的直线，将直线旋转，这条会卡在线段的端点，所以可以枚举这两个端点

，形成一条直线，然后检查这条直线是否穿过其它所有线段

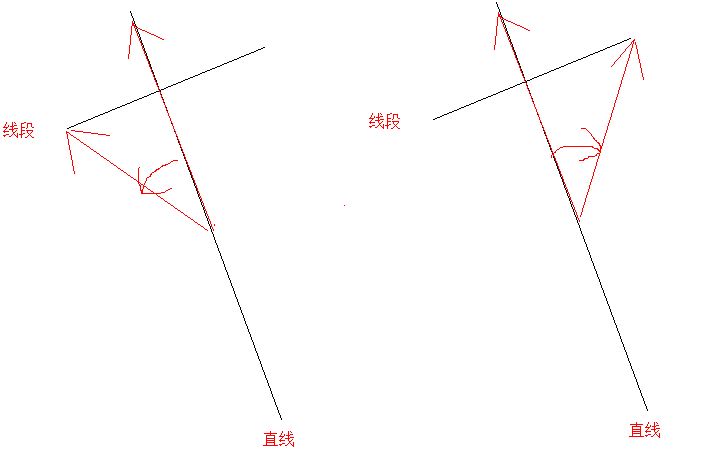
如果穿过，则这两个向量叉积符号相反

#include <iostream>
#include <cmath>

using namespace std;
#define int long long
#define rep(i, l, r) for(int i = l; i <= (int)r; i ++)
#define pb push_back
const int N = 2e5 + 5;
#define x first
#define y second
#define PDD pair<double, double>
const double eps = 1e-8;

int n;
PDD a[N], b[N], p[N];
bool is__same(PDD A, PDD B) {
    return fabs(A.x - B.x) < eps && fabs(A.y - B.y) < eps;
}
double cross(PDD A, PDD B) {// vector(A) * vector(B)
    return A.x * B.y - B.x * A.y;
}
double area(PDD o, PDD a, PDD b) {// vector(OA) * vector(OB)
    // PDD A = {a.x - o.x, a.y - o.y};
    // PDD B = {b.x - o.x, b.y - o.y};
    PDD A, B;
    A.x = a.x - o.x, A.y = a.y - o.y;
    B.x = b.x - o.x, B.y = b.y - o.y;
    return cross(A, B);
}
int sign(double x) {
    if(fabs(x) < eps) return 0;
    if(x < 0) return -1;
    if(x > 0) return 1;
}
bool check() {
    for(int i = 1; i <= 2 * n; i ++) {
        for(int j = i + 1; j <= 2 * n; j ++) {
            if(is__same(p[i], p[j])) continue;
            bool ok = true;
            for(int k = 1; k <= n; k ++) {
                if(sign(area(p[i], p[j], a[k])) * sign(area(p[i], p[j], b[k])) > 0) {
                    ok = false;
                    break;
                }
            }
            if(ok) return true;
        }
    }
    return false;
}
void solve() {
    cin >> n;
    for(int i = 1, k = 1; i <= n; i ++) {
        double x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        // a[i] = {x1, y1}, b[i] = {x2, y2};
        a[i].x = x1, a[i].y = y1;
        b[i].x = x2, b[i].y = y2;
        // p[k ++] = {x1, y1};
        p[k].x = x1, p[k ++].y = y1;
        // p[k ++] = {x2, y2};
        p[k].x = x2, p[k ++].y = y2;
    }
    cout << (check() ? "Yes!\n" : "No!\n");
}
main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int _ = 1;
    cin >> _;
    while(_ --) {
        solve();
    }
    return 0;
}