概述

树状数组是一种数据结构，基本操作有单点修改与查询前缀和，时间复杂度都为$O(logN)$
其思想核心是$c[x]=\sum_{i=x-lowbit(x)+1}^{x}{a[i]}$
下面这题考察了树状数组最基本的两个操作，在进一步深入前需要弄清此题
动态求连续区间和

深入

树状数组与逆序对

虽然归并排序可以求解逆序对数量，但归并排序会对原数组进行改变，而树状数组可以在不改变原数组的情况下求出逆序对数量
其思想主要是维护权值的前缀和：
$1$.逆序扫描数组，对于当前数$a[i]$，$ans+=query(a[i]-1)$，表示比$a[i]$小的数有多少个
$2$.$add(a[i],1)$，相当于$a[i]$这个数又出现了一次
由于是对于权值前缀和的维护，往往树状数组求逆序对要与离散化结合(否则数组会爆)
相关题有： 逆序对的数量 楼兰图腾

树状数组的扩展应用

虽然树状数组的基础操作仅支持单点修改与区间查询，但通过与差分知识的结合，也能实现区间修改和区间查询这两个操作
相关题有： 一个简单的整数问题I 一个简单的整数问题II

树状数组上二分

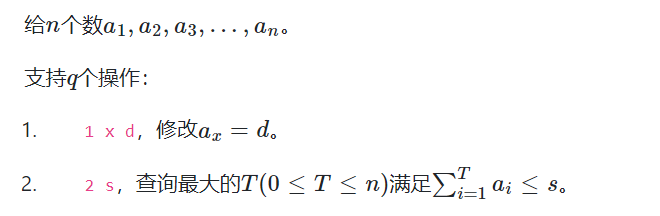
考虑上图这个问题，最直观的想法可能是树状数组查询前缀和+二分答案，这样的时间复杂度为$O(log^2N)$，二分一个$log$，树状数组又一个$log$
但其实可以直接在树状数组上二分，时间复杂度为$O(logN)$(说是二分，感觉更像倍增)
代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int n, q;
int a[N];
LL c[N];
void add(int x, int t)
{
    for (; x <= n; x += x & -x)
        c[x] += t;
}
LL query(LL s) //返回最大的满足条件的T
{
    LL pos = 0;
    for (int j = 18; j >= 0; j--) //2^18大于2e5+10
    {
        if (pos + (1 << j) <= n && c[pos + (1 << j)] <= s)
        {
            pos += 1 << j;
            s -= c[pos];
        }
    }
    return pos;
}
int main()
{
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        add(i, a[i]);
    }
    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            int x, d;
            cin >> x >> d;
            add(x, d - a[x]);
            a[x] = d;
        }
        else
        {
            LL s;
            cin >> s;
            cout << query(s) << '\n';
        }
    }
    return 0;
}

看了代码可以再结合树状数组的形状理解，在进行的工作就是不断缩小答案的区间范围
相关题有： 谜一样的牛

二维树状数组(更高维同理)

一个不怎么用的知识点，即使是二维也很少用。其实十分简单，代码一看便懂，一维树状数组维护了一维的前缀和，那么二维树状数组维护的就是矩阵的前缀和，时间复杂度为$O(log^2N)$。高维树状数组的维度为$x$，时间复杂度就为$O(log^xN)$
模板题： 打鼹鼠