历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

线段树复习笔记

作者：

真我Elysia , 2022-07-21 20:11:41 , 所有人可见 , 阅读 217

2

1

线段树

参考笔记：
算法竞赛进阶指南
orz
orz
or2

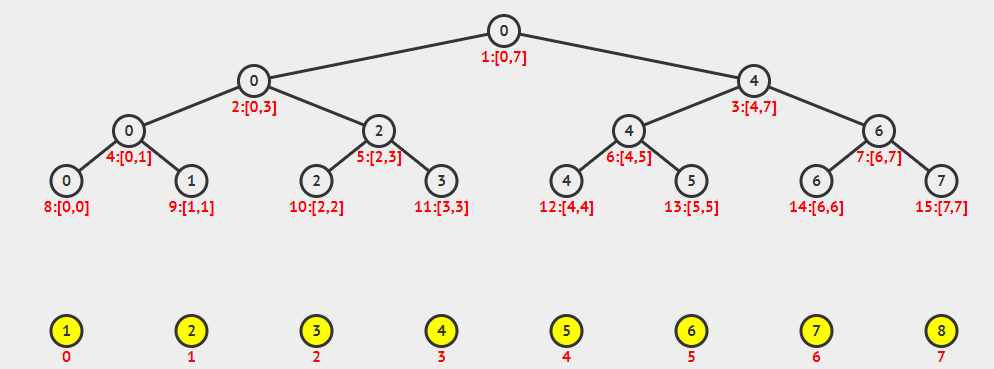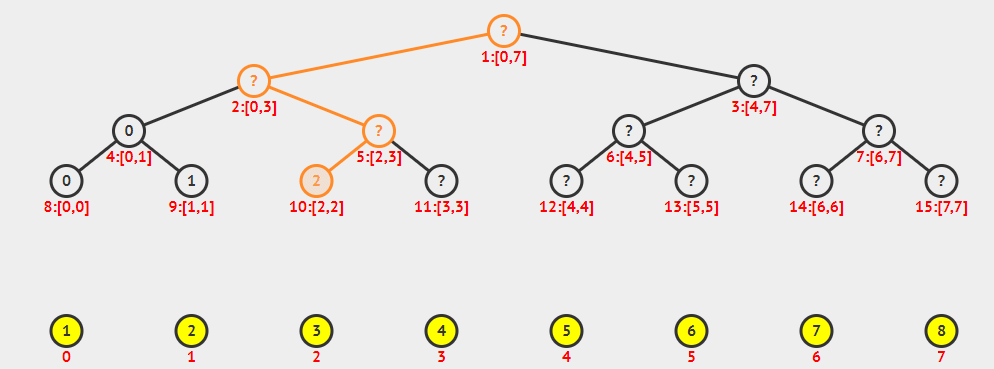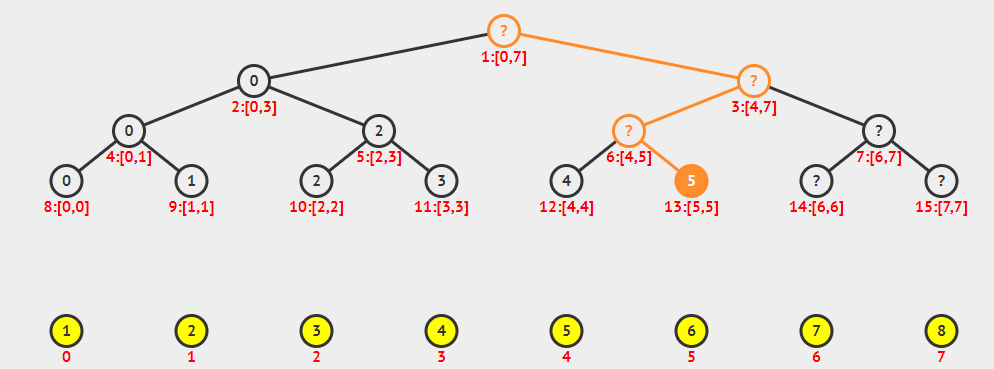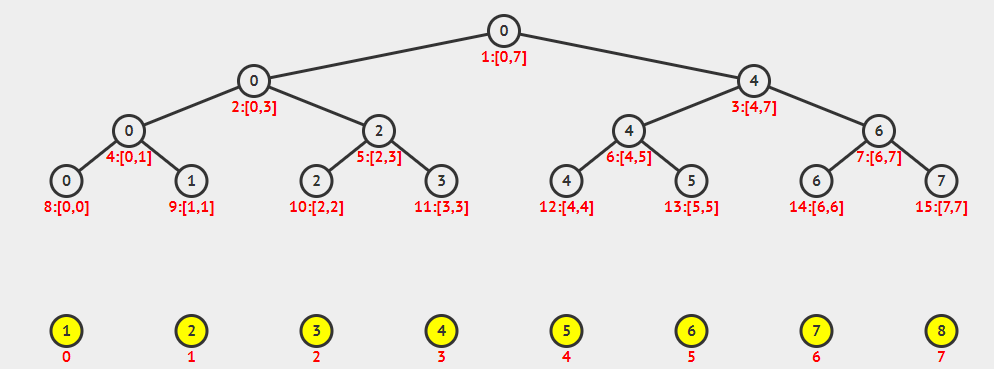
线段树是基于分治思想的数据结构，用于在区间上进行信息统计。

树中的每个节点都代表一个区间。
线段树具有唯一的根节点。
每个叶子节点都代表一个长度为1的元区间[x,x]。
每个内部节点[l,r]，左节点为[l,,mid]，右节点为[mid+1,r]，mid = l+r >> 1。

编号为x , 父节点为x/2 = x >> 1 , 左儿子为2*x = x << 1 , 右儿子为2*x+1 = x << 1|1 。

感谢秦佬笔记中的图。orz

线段树是一个满二叉树。N个节点的满二叉树有2*N+1个节点。
所以线段树的空间通常要开4N。

线段树的基本功能是对序列进行维护，支持查询与修改。

基本操作：

pushup,pushdown
build
modify
- 单点修改
- 区间修改（延迟更新）
- 等等
query

pushup由儿子更新父亲节点的数值。
pushdown由父亲节点向下更新儿子节点。
区间修改需要懒标记。

核心代码

给定长度为N的序列A。
在区间[1,N]上建立线段树，每个节点[i,i]保存A[i]的值。
u代表当前节点的编号。

线段树的创建

以存储区间最大值为例


struct tree{
    int l,r;
    int v;
}tr[N*4];

void build( int u , int l , int r )
{
    tr[u] = {l,r};
    if( l == r ){ tr[u].v = a[l]; return; }
    int mid = l+r >> 1;
    build( u<<1 , l , mid );
    build( u<<1|1 , mid+1 , r );
}

单点修改

O(logN)
从根节点出发，递归找到带表区间[x,x]的叶节点，然后往上跟新[x,x]以及它的所有祖先节点上保存的信息。


void pushup( int u )
{
    tr[u].v = max( tr[u<<1].v , tr[u<<1|1].v );
}

void modify( int u , int x , int v )
{
    if( tr[u].l == x && tr[u].r == x ) tr[u].v = v;
    else 
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if( x <= mid ) modify( u<<1 , x , v );
        // x属于左半边区间
        else modify( u<<1|1 , x , v );
        // x属于右半边区间
        pushup( u );//从下往上更新数据
    }    
}

区间查询

例如查找区间[l,r]的最大值。

若[l,r]完全覆盖了当前节点代表的区间，则立即回溯，并选择当前节点的数据作为候选。
若左子节点与[l,r]有重叠部分，则递归访问左子节点。
若右子节点与[l,r]有重叠部分，则递归访问右子节点。

int query( int u , int l , int r )
{
    if( tr[u].l >= l && tr[u].r <= r ) 
        return tr[u].v;
    int mid = tr[u].l+tr[u].r >> 1;
    int v = 0;
    if( mid >= l ) v = max( v , query( u<<1 , l , r ) );
    if( mid < r ) v = max( v , query( u<<1|1 , l , r ) );

    return v;
}

例题：

245. 你能回答这些问题吗

给定长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

1 x y，查询区间 [x,y] 中的最大连续子段和，即 maxx≤l≤r≤y{∑i=lrA[i]}。
2 x y，把 A[x]改成 y。

对于每个查询指令，输出一个整数表示答案。

思路：

int l, r, lmax, rmax, tmax, sum;
// lmax最大前缀和，rmax最大后缀和，tmax最大连续子段和，sum区间总和

最大连续子段和，分为横跨两个区间和在一个区间中。
横跨两个区间：左子区间的最大后缀和+右子区间的最大前缀和。
维护前缀和：

只有左边的lmax
l.sum + r.lmax

const int N = 1e6+10;

int a[N];
int n,m,p;

struct Node{
    int l,r;
    int sum,lmax,rmax,tmax;
}tr[N*4];

void pushup( Node &u , Node &l , Node &r )
{
    u.sum = l.sum+r.sum;
    //当前总字段和
    u.lmax = max( l.lmax , l.sum+r.lmax );
    //前缀和 max(左子区间前缀和，左子区间总和+右子区间前缀和)
    u.rmax = max( r.rmax , r.sum+l.rmax );
    //后缀和 max(右子区间后缀和，右子区间总和+左子区间后缀和)
    u.tmax = max( max( l.tmax , r.tmax ) , l.rmax+r.lmax );
    //区间最大值 max(左子区间前缀和，右子区间后缀和，
    //(左子区间后缀和+右子区间前缀和) )
}

void pushup( int u )
{
    pushup( tr[u] , tr[u<<1] , tr[u<<1|1] );
}

void build( int u , int l , int r )
{
    if( l == r ) tr[u] = { l , r , a[l] , a[l] , a[l] , a[l] };
    else 
    {
        tr[u] = {l,r};//易错点，之前没写这个一直错。QAQ
        int mid = (l+r) >> 1;
        build( u<<1 , l , mid );
        build( u<<1|1 , mid+1 , r );
        pushup( u );
        //更新信息
    }
}

//查询，由于存在跨左右子区间的情况，返回结构体类型，再用pushup计算结果
//感觉有点难理解QAQ
Node query( int u , int l , int r )
{
    // 当前u所在区间在[l,r]中，直接结束递归。
    if( l <= tr[u].l && tr[u].r <= r )
        return tr[u];
    int mid = (tr[u].l+tr[u].r) >> 1;
    Node res;
    if( r <= mid ) res = query( u<<1 , l , r );
    // 当r<=mid时，递归左子树。不懂可以画出线段树。
    else if( l > mid ) res = query( u<<1|1 , l , r );
    // 当l>mid，递归右子树。
    else 
    {   
        // 当前的最大连续子段和横跨[l,mid],[mid+1,r]时，进行下列操作
        Node left = query( u<<1 , l , r );
        Node right = query( u<<1|1 , l , r );
        pushup( res , left , right );
    }
    return res;
}

void modify( int u , int x , int k )  
{
    if( tr[u].l == x && tr[u].r == x )
    {
        //到达根节点时不用pushup。QAQ
        //之前理解错了，在这里又pushup一次。
        tr[u] = { x , x , k , k , k , k };
    }else 
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if( mid >= x ) modify( u<<1 , x , k );
        else modify( u<<1|1 , x , k );
        pushup( u );
    }

}

int main(){
    scanf("%d%d",&n,&m);
    for( int i = 1 ; i <= n ; i++ )
        scanf("%d",&a[i]);
    build( 1 , 1 , n );
    while( m-- )
    {
        int t,x,y;
        scanf("%d%d%d",&t,&x,&y);
        if( t == 1 ) 
        {
            if( x > y ) swap( x , y );
            int ans = query(1,x,y).tmax;
            printf("%d\n",ans);
        }else{
            modify( 1 , x , y );
        }
    }
    return 0;
}

246. 区间最大公约数

给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

C l r d，表示把 A[l],A[l+1],…,A[r]都加上 d。
Q l r，表示询问 A[l],A[l+1],…,A[r] 的最大公约数(GCD)。

对于每个询问，输出一个整数表示答案。

思路：
参考博客
当初这道题目时还以为是区间更新，听了Y总的讲解后才知道用差分的思想去解决这种问题
能不用懒标记就不要用，懒标记太容易出错。QAQ

区间更新：可以使用差分的思想，也就是将待更新的[l,r]区间，前端l加上d，后端r+1处-d。
求区间[l,r]的最大公约数。

区间更新

$gcd( a[1] , a[2] , .... a[n] ) = gcd( a[1] , a[2]-a[1] , .... a[n] -a[n-1] ) = gcd( a[1] , gcd( b[2] , b[3] , … , b[n] ) )$

b数组为差分数组，所以我们可以将区间更新转换为单点更新。（妙啊~）

区间查询
我们只需要查询出a[l]和gcd( b[2] , b[3] , … b[n] )即可。
$gcd( a[l] ) = gcd( b[1]+b[2]+…+b[l] )$

刚开始写的时候wa了几次，找了两个小时才发现是数组开小了。QAQ

const int N = 6e5+10;

int n,m;
LL a[N];

struct Node{
    int l,r;
    LL sum,d;
}tr[N*4];

LL gcd(LL a, LL b)  
{//求最大公约数
    return b ? gcd(b, a % b) : a;
}

void pushup( Node &u , Node &l , Node &r )
{
    //更新数据
    u.sum = l.sum+r.sum;
    u.d = gcd( l.d , r.d );
}

void pushup( int u )
{
    pushup( tr[u] , tr[u<<1] , tr[u<<1|1] );
}

void build( int u , int l , int r )
{
    //建树一定要建边界。
    tr[u].l = l , tr[u].r = r;
    if( l == r )
    {
        LL b = a[l]-a[l-1];
        tr[u].sum = b , tr[u].d = b;
    }else{
        int mid = (l+r) >> 1;
        build( u<<1 , l , mid );
        build( u<<1|1 , mid+1 , r );
        //切记pushup
        pushup( u );
    }
}

void modify( int u , int x , LL v )
{
    if( tr[u].l == x && tr[u].r == x )
    {
        tr[u].d = tr[u].sum+v;
        tr[u].sum += v;
    }
    else 
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if( mid >= x ) modify( u<<1 , x , v );
        else modify( u<<1|1 , x , v );
        pushup( u );
    }
}

Node query( int u , int l , int r )
{
    if( tr[u].l >= l && tr[u].r <= r )
    {
        return tr[u];
    }else
    {
        int mid = (tr[u].l + tr[u].r) >> 1;
        if( mid >= r ) return query( u<<1 , l , r );
        else if( mid < l ) return query( u<<1|1 , l , r );
        else 
        {
            Node res;
            Node left = query( u<<1 , l , r );
            Node right = query( u<<1|1 , l , r );
            pushup( res , left , right );
            return res;
        }
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for( int i = 1 ; i <= n ; i++ ) scanf("%lld",&a[i]);
    build( 1 , 1 , n );
    while( m-- )
    {
        char op[2];
        int l,r;LL d;
        scanf("%s%d%d",op,&l,&r);
        if( *op == 'C' )
        {
            scanf("%lld",&d);
            modify( 1 , l , d );
            if( r+1 <= n ) modify( 1 , r+1 , -d );
        }else{
            Node left = query( 1 , 1 , l );
            Node right = { 0 , 0 , 0 , 0 };
            if( l+1 <= r ) right = query( 1 , l+1 , r );
            printf("%lld\n",abs( gcd( left.sum , right.d ) ));
        }
    }
    return 0;
}

懒标记pushdown

懒标记同时也被称为延迟标记。
标记到父亲节点，再由父亲节点向下更新。

不到万不得以时不更新数据。将要修改的点我们先把他们屯在一起，直到要查询时才去更新。

例题

区间加法线段树
AcWing 243. 一个简单的整数问题2

给定一个长度为 N 的数列 A，以及 M 条指令，每条指令可能是以下两种之一：

C l r d，表示把 A[l],A[l+1],…,A[r]都加上 d。
Q l r，表示询问数列中第 l∼r 个数的和。

对于每个询问，输出一个整数表示答案。

区间加法

typedef long long LL;
const int N = 5e5+10;

int a[N];
int n,m;

struct Node{
    int l,r;
    LL sum,add;
}tr[N*4];

void pushup( int u )
{
    tr[u].sum = tr[u<<1].sum + tr[u<<1|1].sum;
}

void pushdown( int u )
{
    Node &t = tr[u] , &left = tr[u<<1] , &right = tr[u<<1|1];
    if( t.add )
    {
        left.add += t.add  , left.sum += (left.r-left.l+1)*t.add;
        right.add += t.add , right.sum += (right.r-right.l+1)*t.add;
        t.add = 0; 
    }   
}

void build( int u , int l, int r )
{
    if( l == r ) 
    {
        tr[u] = {l,r,a[l],0};
    }else {
        tr[u] = {l,r};
        int mid = l+r >> 1;
        build( u<<1 , l , mid );
        build( u<<1|1 , mid+1 , r );
        pushup( u );
    }
}

void modify( int u , int l , int r , LL x )
{
    if( tr[u].l >= l && tr[u].r <= r ) 
    {
        tr[u].sum += (tr[u].r-tr[u].l+1)*x;
        tr[u].add += x;
    }
    else 
    {
        pushdown( u );
        int mid = tr[u].l+tr[u].r >> 1;
        if( mid >= l ) modify( u<<1 , l , r , x );
        if( mid < r ) modify( u<<1|1 , l , r , x );
        pushup( u );
    }
}

LL query( int u , int l , int r )
{
    if( tr[u].l >= l && tr[u].r <= r )
    {
        return tr[u].sum;
    }
    pushdown( u );
    LL res = 0;
    int mid = tr[u].l + tr[u].r >> 1;
    if( mid >= l ) res += query( u<<1 , l , r );
    if( mid < r ) res += query( u<<1|1 , l , r );

    return res;
}

int main(){
    scanf("%d%d",&n,&m);
    for( int i = 1 ; i <= n ; i++ ) scanf("%d",&a[i]);

    build( 1 , 1 , n );

    while( m-- )
    {
        char op[3];
        int l,r;LL d;
        scanf("%s%d%d",op,&l,&r);
        if( *op == 'C' )
        {
            scanf("%lld",&d);
            modify( 1 , l , r , d );
        }else 
        {
            printf("%lld\n", query( 1 , l , r ) );
        }
    }
    return 0;
}

区间乘法线段树
AcWing 1277. 维护序列

有长为 N 的数列，不妨设为 a1,a2,…,aN。

有如下三种操作形式：

把数列中的一段数全部乘一个值；
把数列中的一段数全部加一个值；
询问数列中的一段数的和，由于答案可能很大，你只需输出这个数模 P 的值。

QAQ感觉很奇特，我都开LL了，但是第7个点还是过不去，直到我把eval函数中的乘法更新全部加上(LL)就过来。
有点玄学。

本题的难点在乘法线段树的lazy更新上。
我们可以把乘或加的操作都看成 x * c + d。
比如：

乘法：xc+0。加法：x1+c。

懒标记的更新：

原式：x*mul+add
更新后
( x*mul + add ) * c + d
-> x*mul*c + add*c+d

这里要是理解后还是挺简单的。
虽然改了挺久的。这可能就是事后诸葛亮吧。无奈😔

typedef long long LL;

const int N = 4e5+10;

int n,m,p;
int a[N];

struct Node{
    int l,r;
    LL sum,add,mul;
}tr[4*N];

// 懒标记更新
void eval( Node &u , int add , int mul )
{
    u.sum = ( (LL)u.sum*mul + (LL)(u.r-u.l+1)*add )%p;
    u.mul = (LL)u.mul*mul%p;
    u.add = (LL)(u.add*mul+add)%p;
}

// 左右两个区间分别更新
// 将当前区间的标记初始化
void pushdown( int u )
{   
    eval( tr[u<<1] , tr[u].add , tr[u].mul );
    eval( tr[u<<1|1] , tr[u].add , tr[u].mul );
    tr[u].add = 0;
    tr[u].mul = 1;
}

void pushup( int u )
{
    tr[u].sum = ( tr[u<<1].sum + tr[u<<1|1].sum )%p;
}

void build( int u , int l , int r )
{
    tr[u].l = l , tr[u].r = r;
    if( l == r )
    {
        tr[u].sum = a[l];
        tr[u].add = 0;
        tr[u].mul = 1;
    }else
    {
        tr[u].add = 0;
        tr[u].mul = 1;
        int mid = (l+r) >> 1;
        build( u<<1  , l , mid );
        build( u<<1|1 , mid+1 , r );
        pushup( u );
        // 每次建树后pushup
    }
}

void modify( int u , int l , int r , int mul , int add )
{
    if( tr[u].l >= l && tr[u].r <= r )
    {
        eval( tr[u] , add , mul );
    }else
    {
        // 区间分裂前，先将懒标记下放进行更新。
        pushdown( u );
        int mid = (tr[u].l + tr[u].r) >> 1;
        if( l <= mid ) modify( u<<1 , l , r , mul , add );
        if( r > mid ) modify( u<<1|1 , l , r , mul , add );
        pushup( u );
        // 最后pushup一次来更新区间的和。
    }
}

LL query( int u , int l , int r )
{
    if( tr[u].l >= l && tr[u].r <= r ) 
        return tr[u].sum;

    pushdown( u );
    int mid = (tr[u].l + tr[u].r) >> 1;
    LL res = 0;
    if( l <= mid ) res += query( u<<1 , l , r );
    if( r > mid ) res = (res + query( u<<1|1 , l , r ))%p;
    return res;
}

int main()
{
    scanf("%d%d",&n,&p);
    for( int i = 1 ; i <= n ; i++ ) scanf("%d",&a[i]);
    build( 1 , 1 , n );
    scanf("%d",&m);
    while( m-- )
    {
        int x,t,g,c;
        scanf("%d%d%d",&x,&t,&g);
        if( x == 1 )
        {
            scanf("%d",&c);
            modify( 1 , t , g , c , 0 );
        }else if( x == 2 )
        {   
            scanf("%d",&c);
            modify( 1 , t , g , 1 , c );
        }else{
            printf("%lld\n",query(1,t,g)%p);
        }
    }

    return 0;
}

扫描线以后有机会再写

线段树的应用

https://www.acwing.com/activity/content/problem/content/1611/

题意：

有几个古希腊书籍中包含了对传说中的亚特兰蒂斯岛的描述。

其中一些甚至包括岛屿部分地图。

但不幸的是，这些地图描述了亚特兰蒂斯的不同区域。

您的朋友 Bill 必须知道地图的总面积。

你自告奋勇写了一个计算这个总面积的程序。

输入格式

输入包含多组测试用例。

对于每组测试用例，第一行包含整数 n

，表示总的地图数量。

接下来 n 行，描绘了每张地图，每行包含四个数字 x1,y1,x2,y2（不一定是整数），(x1,y1) 和 (x2,y2) 分别是地图的左上角位置和右下角位置。

注意，坐标轴 x 轴从上向下延伸，y 轴从左向右延伸。

当输入用例 n=0 时，表示输入终止，该用例无需处理。

输出格式

每组测试用例输出两行。

第一行输出 Test case #k，其中k
是测试用例的编号，从 1

开始。

第二行输出 Total explored area: a，其中 a

是总地图面积（即此测试用例中所有矩形的面积并，注意如果一片区域被多个地图包含，则在计算总面积时只计算一次），精确到小数点后两位数。

在每个测试用例后输出一个空行。

贴个大佬的代码日后复习
https://www.acwing.com/solution/content/49051/

0 评论

App 内打开

线段树 复习笔记

线段树