摘自：超级卡特兰数（又称大施罗德数）
百度百科： 施罗德数

在组合数学中，施罗德数用来描述从 $(0,0)$ 到 $(n,n)$ 的网格中，只能使用 $(1,0)、(0,1)、(1,1)$ 三种移动方式，始终位于对角线下方且不越过对角线的路径数。

施罗德数的前几项(从第 $0$ 项算起)为 $1, 2, 6, 22, 90, 394, 1806, 8558, 41586, 206098$……
(OEIS A006318)

下图为 $n = 1, 2, 3$ 时的施罗德路径

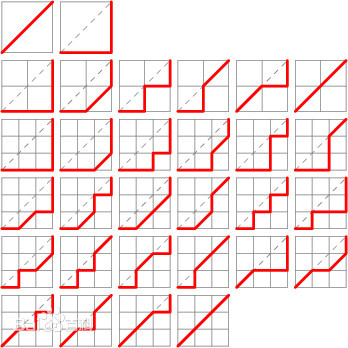
施罗德数的递推公式为

$$S_i = S_{i - 1} + \sum_{j = 0}^{i - 1}S_jS_{n - j - 1}$$

不过 $O(n^2)$ 的递推在 $1e5$级别的数据面前显然是要超时的

有递推式

$$(i + 1)F_i = (6n - 3)F_{i - 1} - (i - 2)F_{i - 2}$$

使得 $F_0 = S_0$，对于任意的 $i \geq 1$ 都有 $2F_i = S_i$

C++ 代码

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

typedef long long LL;

const int N = 100010, mod = 1e9 + 7;

int qmi(int a, int k)
{
    int res = 1;
    while(k)
    {
        if(k & 1)  res = (LL)res * a % mod;
        k >>= 1;
        a = (LL)a * a % mod;
    }
    return res;
}

LL f[N], s[N];
void init(int n)
{
    f[0] = s[0] = f[1] = 1;
    s[1] = 2;
    for(int i = 2; i <= n; i ++)
    {
        f[i] = ((6 * i - 3) * f[i - 1] - (i - 2) * f[i - 2]) % mod * qmi(i + 1, mod - 2) % mod;
        s[i] = f[i] * 2 % mod;
    }
}

int main()
{
    init(N - 1);

    for(int i = 0; i < 10; i ++)  printf("%d\n", s[i]);
    return 0;
}