算法思路

假设目标值在闭区间 [left, right] 中， 每次将区间长度缩小一半，当 left == right 时，就找到了目标值。

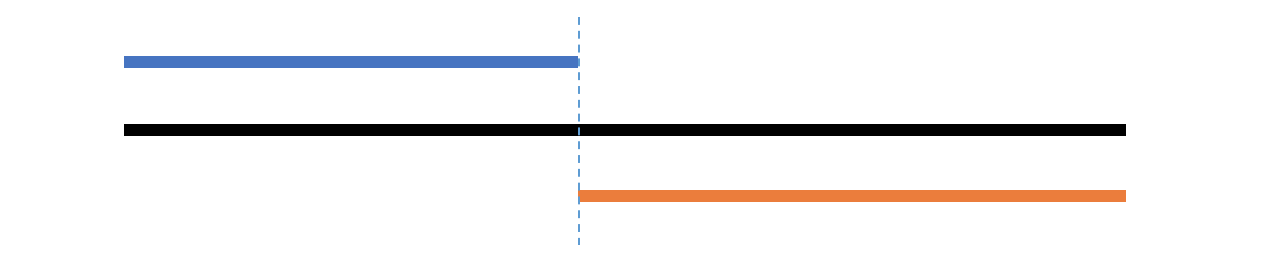
模板 1

目标值 = 红色区间的第一个值。

如果 middle 落在红色区间，则有

$$[L, R] \rightarrow [L, M]$$

$$R = M$$

反之，middle 落在蓝色区间，则有

$$[L, R] \rightarrow [M + 1, R]$$

$$L = M + 1$$

模板 1 中，middle 的更新 = 边界中值的向下取整

$$M = \biggl\lfloor \frac{L + R}{2} \biggr\rfloor$$

// 二分查找 模板 1
int binarySearch(vector<int>& a, int target) {
    int left = 0;
    int right = a.size() - 1;

    while (left < right) {
        int middle = (left + right) >> 1;
        if (isRed(a[middle]))
            right = middle;
        else
            left = middle + 1;
    }

    return left;
}

模板 2

目标值 = 蓝色区间的最后一个值。

如果 middle 落在蓝色区间，则有

$$[L, R] \rightarrow [M, R]$$

$$L = M$$

反之，middle 落在红色区间，则有

$$[L, R] \rightarrow [L, M - 1]$$

$$R = M - 1$$

模板 2 中，middle 的更新 = 边界中值的向上取整

$$M = \biggl\lceil \frac{L + R}{2} \biggr\rceil$$

// 二分查找 模板 2
int binarySearch(vector<int>& a, int target) {
    int left = 0;
    int right = a.size() - 1;

    while (left < right) {
        int middle = (left + right + 1) >> 1;    // 防止死循环
        if (isBlue(a[middle]))
            left = middle;
        else
            right = middle - 1;
    }

    return left;
}

模板 3

ALGS4 上的二分查找的代码，适用于判断确切的某一个目标值是否在区间内的情况，不需要考虑如何切分区间。

// 二分查找 模板 3
int binarySearch(vector<int>& a, int target) {
    int left = 0;
    int right = a.size() - 1;

    while (left <= right) {
        int middle = (left + right) >> 1;
        if (a[middle] < target)
            middle = left + 1;
        else if (a[middle] > target)
            middle = right - 1;
        else
            return middle;
    }

    return -1;
}