$树状数组$

前言

一般树状数组适用于一种可差分，满足结合律的运算。

可差分：对于此运算，有一个逆运算与之对应。(例如 $xor$ 满足而 $gcd$ 不满足)
结合律：(a O b) O c = a O (b O c) （ $O$ 代表运算）

解决问题

• 单点修改
• 区间求和

方法一(暴力算法)

• 单点修改 $O(1)$
• 区间修改 $O(n)$
• 总时间复杂度$O(nm)$

方法二(树状数组)

• 单点修改 $O(logn)$
• 区间修改 $O(logn)$
• 总时间复杂度$O(mlogn)$

$树状数组$

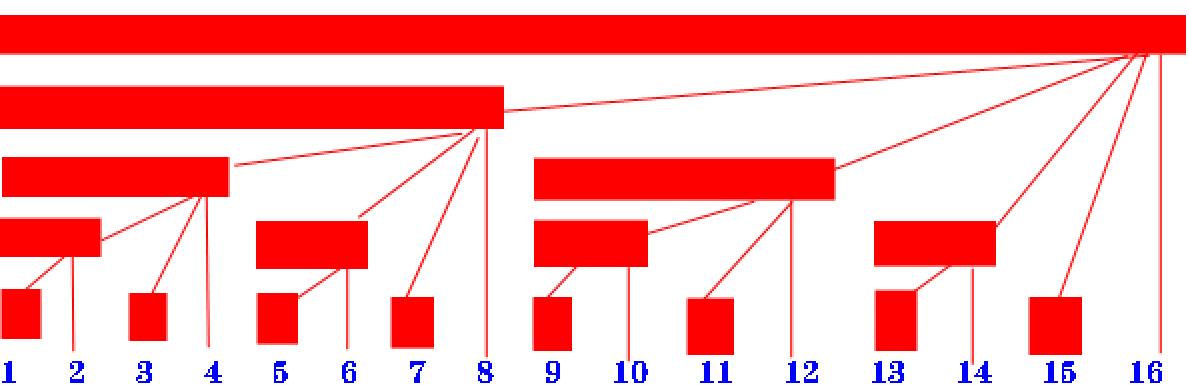
设 $tr[x]$ 为 以第 $x$ 位结尾的长度为 $lowbit(x)$ 的所有数字之和

$lowbit(x):$ 表示 $x$ 最右边的 $”1”$ 所对应的值

如图, $tr[2]=A[1]+A[2]$

$tr[4] = A[1]+A[2]+A[3]+A[4]$

$tr[16] = A[1]+A[2]+…+A[16]$

$单点修改$

$如图,如果想对点 x 进行修改 , 那么包含 x 的所有点的 tr 值都会 对应的改变$

$即从 根结点 出发 走向 x 的路径上的所有点$

$x = 5 时,16 -> 8 -> 6 -> 5$

$根据树状数组的性质,x的父节点是x+lowbit(x)$

void add(int x, int k)
{
    for (int i = x; i <= n; i += lowbit(i))
        tr[i] += k;
}

$区间求和$

$利用前缀和,区间 [l, r] 的数字之和等于 sum[r] - sum[l] $

$假设现在要求sum(x),$

$C[x] 表示区间 [x-lowbit(x)+1, x] 的数字之和$

$那么C[x]的第一个没有累加的点就是 x-lowbit(x)$

$sum[x] = sum[x - lowbit(x)] + c[x]$

int sum(int x){
    int res = 0;
    for (int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;    
}

Update on 2023/1/31 ，以下内容为补充内容，都以加法为例。

$树状数组变形1$

支持 $区间修改\times 单点查询$ 。

设差分数组 $d[i] = a[i] - a[i - 1]$

区间修改变为单点修改，单点查询则变为区间查询。

$树状数组变形2$

支持 $区间修改\times 区间查询$

设差分数组 $d[i] = a[i] - a[i - 1]$

区间修改变为单点修改。

区间查询 $[l, r] = sum[r] - sum[l - 1]$ 。

$sum_r = \sum_{i=1}^{r} \sum_{j=1}^{i} d[j] = \sum_{i = 1}^{r} d[i] \times (r - i + 1) = (r+1) \sum_{i=1}^{r} d[i] - \sum_{i=1}^{r} d[i] \times i$

再开一个树状数组维护 $d[i]\times i$ 即可。

$树状数组变形3$

支持 $二维树状数组的单点修改\times 区间查询$

$c(x,y)$ 表示以 $(x,y)$ 为右下角，高 $lowbit(x)$ ，宽 $lowbit(y)$ 的矩阵的和。

设 $Z(x)$ 表示在一维树状数组下，$x$ 的所有祖先。

修改 $(x,y)$ 会影响所有 $x’ \in Z(x)$ 且 $y\in Z(y)$ 。

区间查询 $[x1,y1,x2,y2] = sum_{x2,y2} - sum_{x2, y1 - 1} - sum_{x1 - 1, y2} + sum_{x1-1,y1-1}$ （左上角和右下角）

$sum_{x,y} = sum_{x - lowbit(x), y} + sum_{x, y - lowbit(y)} - sum_{x-lowbit(x),y-lowbit(y)} + c(x,y)$

$树状数组变形4$

支持 $二维树状数组的 区间修改\times 区间查询$

同 $变形2$ 。

$树状数组变形5$

支持 $不可差分的运算$ ，单次时间复杂度 $O(log^2 n)$

查询 $[l,r]$

每次若 $r - lowbit(r) + 1\ge l$ ，则 $res$ 加上 $c(r)$

否则 $res$ 加上单点 $a(r)$ ，$r$ 减 $1$ 。

感谢观看！