T1

题目描述

$Q$哥在玩一个游戏，他刚打完这个游戏的一场战役并获得了足够多的金币进行下一场战役，这场战役一共有$n$个怪物，击杀第$i$个怪物需要花费$c_i$的血量，同时获得$w_i$的金币，在战役的最开始$Q$哥可以花费金币来购买血量，只有在当场战役购买的血量才对该场战役有效。$Q$哥想知道他接下来的这场战役最多能多获得多少金币。

输入描述

第一行数字$n$表示怪物个数和每个金币能够买的血量。
接下来$n$行，每行两个数字，第$i$行为$c_i$和$w_i$，含义如题所示。
$1 \leq n \leq 1000 \\\\ 1 \leq m \leq 1e^9 \\\\ 1 \leq w_i \leq 100 \\\\ 1 \leq c_i \leq 1e^6 \\\\ $

输出描述：

一行一个数字表示答案，即$Q$哥的最大收益。

样例1

输入：

3 2
1 1
1 10
3 1

输出：

10

说明：

样例一表示有三个怪物，$Q$哥可以选择开局花费一个金币购买2点血量，然后击杀第一个和第二个怪物共获得11个金币，总收益为10.

样例2

输入：

1 2
3 1

输出：

0

说明：

请注意当怪物的收益比花费要低时，$Q$哥可以选择不参加这场战役，这样它的收益为0.

算法

只杀满足$w_i > \frac{c_i}{m}$的怪物，性价比高。

C++ 代码

#include <iostream>
using namespace std;

typedef long long LL;
LL n, m, W, C;

int main() {
    cin >> n >> m;
    while (n -- ) {
        int c, w; cin >> c >> w;
        if (w * m > c) {
            W += w;
            C += c;
        }
    }
    LL ret = W - C / m;
    cout << ret;
    return 0;
}

T2

题目描述

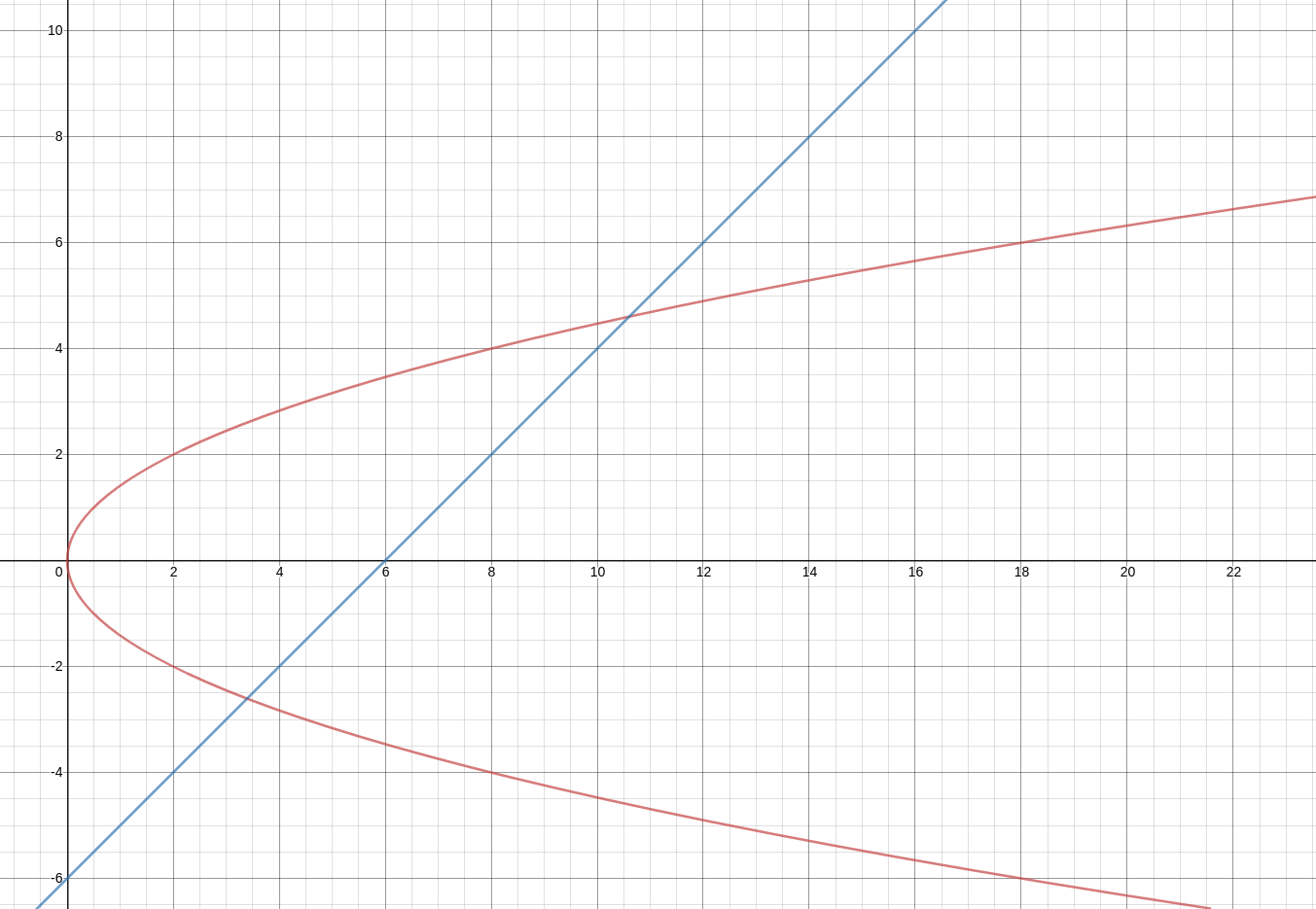
求抛物线$y^2=2Ax$和直线$y=Bx+C$所围成的封闭图形面积。若图形不存在, 则输出0。

输入描述

第一行输入一个正整数T，表示测试数据组数。
接下来每行输入三个整数A、B和C。
$1 \leq A, B \leq 100 \\\\ -100 \leq C \leq 100 \\\\ $

输出描述

每组测试数据输出一个答案。在$\frac{| real - pred |}{real} < 1e^{-4}$范围内都视为正确输出。

样例1

输入：

1
1 1 -6

输出：

31.2481110540

算法(数学题)

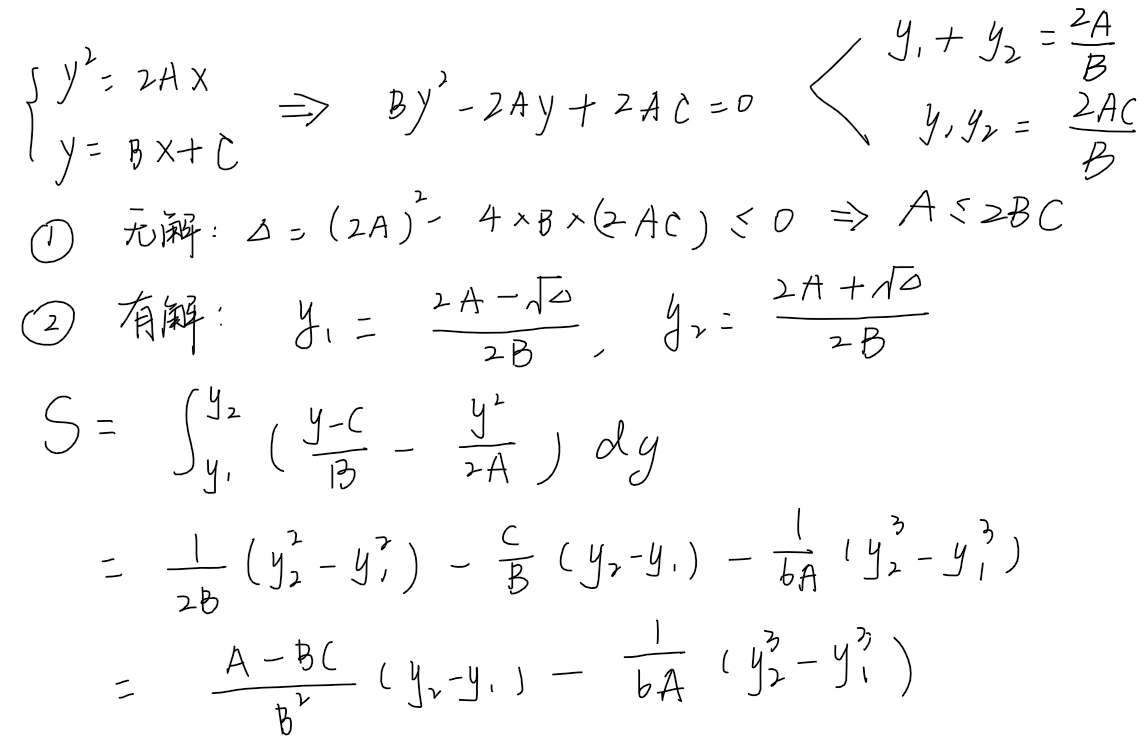
C++ 代码

#include <iostream>
#include <cmath>
using namespace std;

int T, a, b, c;

int main() {
    cin >> T;
    while (T -- ) {
        cin >> a >> b >> c;
        int delta = 4 * a * a - 8 * a * b * c;
        if (delta <= 0) cout << 0 << endl;
        else {
            double y1 = (2 * a - sqrt(delta)) / (2 * b);
            double y2 = (2 * a + sqrt(delta)) / (2 * b);
            double part1 = (a - b * c) / (b * b) * (y2 - y1);
            double part2 = (y2 * y2 * y2 - y1 * y1 * y1) / (6 * a);
            printf("%.10lf\n", part1 - part2);
        }
    }
    return 0;
}

T3

题目描述

$n$个房间里各有一名犯人，每个人从$1 \sim m$中随机选择一个数，若相邻两个房间的犯人的数字相同就会发生冲突，问发生冲突的选择方案有多少个。（由于最后答案可能很大，因此需要对$100003$取模）。

输入描述

第一行输入两个正整数$m$和$n$，含义如题所示。
$1 \leq n \leq 1e^{12} \\\\ 1 \leq m \leq 1e^8 \\\\ $

输出描述：

一行一个数字表示答案，即发生冲突的方案数。

样例1

输入：

2 3

输出：

6

算法(应该也算数学题)

C++ 代码

#include <iostream>
using namespace std;

typedef long long LL;
const int mod = 100003;

int m;
LL n;

int qmi(int a, LL k) {
    int ret = 1;
    while (k) {
        if (k & 1) ret = (LL)ret * a % mod;
        a = (LL)a * a % mod;
        k >>= 1;
    }
    return ret;
}

int main() {
    cin >> m >> n;
    cout << (qmi(m, n) - (LL)m * qmi(m - 1, n - 1) % mod + mod) % mod;
    return 0;
}

T4

题目描述

有$n$个物品，每个物品有$k$个属性，第$i$件物品的第$j$个属性用一个正整数表示记为$a_{i,j}$，两个不同的物品$i$、$j$被称为是完美对当且仅当
$$a_{i,1} + a_{j,1} = a_{i,2} + a_{j,2} = \cdots = a_{i,k} + a_{j,k}$$
，求完美对的个数。

输入描述

第一行两个数字$n$和$k$。
接下来$n$行，第$i$行$j$个数字表示$a_{i,j}$。
$1 \leq n \leq 1e^6 \\\\ 2 \leq k \leq 10 \\\\ $

输出描述：

一行一个数字表示答案。

样例1

输入：

5 3
2 11 21
19 10 1
20 11 1
6 15 24
18 27 36

输出：

3

算法（哈希表）

如果把完美对的条件后加上”=0”，那么问题就变成寻找与当前物品属性相反的物品的个数。考虑进行如下转换：
$$a_{i,1} + a_{j,1} = a_{i,2} + a_{j,2} = \cdots = a_{i,k} + a_{j,k} \\\\ \implies (a_{i,2} - a_{i,1}) + (a_{j,2} - a_{j,1}) = \cdots = (a_{i,k} - a_{i,k - 1}) + (a_{j,k} - a_{j,k - 1}) = 0$$
于是属性个数变为$k - 1$，然后用哈希表统计物品个数。全0属性和非全0属性的物品需要分开计算。

C++ 代码

#include <iostream>
#include <vector>
#include <map>
using namespace std;

#define x first
#define y second

const int N = 1e6 + 10, M = 15;

int n, k;
int a[N][M];
vector<vector<int>> b;

int main() {
    cin >> n >> k;

    for (int i = 0; i < n; i ++ ) {
        for (int j = 0; j < k; j ++ )
            cin >> a[i][j];

        vector<int> t;
        for (int j = 1; j < k; j ++ )
            t.push_back(a[i][j] - a[i][j - 1]);

        b.push_back(t); // 新的属性数组，n个物品，k-1个属性
    }

    map<vector<int>, int> m;
    for (auto item : b) m[item] ++ ;

    vector<int> tmp(k - 1, 0);

    int ret_zero = 0;
    if (m[tmp]) {
        int cnt = m[tmp];
        ret_zero += cnt * (cnt - 1) / 2;
        m.erase(tmp);
    }

    int ret_other = 0;
    for (auto item : m) {
        for (int i = 0; i < item.x.size(); i ++ ) tmp[i] = -item.x[i];
        ret_other += m[tmp] * item.y;
    }

    cout << ret_zero + ret_other / 2;

    return 0;
}

T5

题目描述

现在有$10^7$个用户，编号为$1 \sim 10^7$，现在已知有$m$对关系，每一对关系给你两个数$x$和$y$，代表编号为$x$的用户和编号为$y$的用户是在一个圈子中，例如：$A$和$B$在一个圈子中，$B$和$C$在一个圈子中，那么$A$、$B$、$C$就在一个圈子中。现在想知道最多的一个圈子内有多少个用户。

输入描述

第一行输入一个整数$T$，代表接下来有$T$组数据。
对于每一组测试数据：第一行输入1个整数$n$，代表有$n$对关系。
接下来$n$行，每一行输入两个数$a$和$b$，代表编号为$a$和编号为$b$的用户在同一个圈子里。
$1 \leq T \leq 10 \\\\ 1 \leq n \leq 1e^5 \\\\ 1 \leq x, y \leq 1e^7 \\\\ $

输出描述：

对于每组数据，输出一个答案代表一个圈子内的最多人数。

样例1

输入：

2
4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8

输出：

4
2

算法

维护带有集合数量的并查集

C++ 代码

#include <iostream>
using namespace std;

const int N = 1e7 + 10;

int T, n;
int p[N], cnt[N];

int find(int u) {
    if (p[u] != u) p[u] = find(p[u]);
    return p[u];
}

int main() {
    cin >> T;
    while (T -- ) {
        cin >> n;

        for (int i = 1; i <= N; i ++ ) p[i] = i, cnt[i] = 1;

        while (n -- ) {
            int a, b; cin >> a >> b;
            int root_a = find(a), root_b = find(b);
            if (root_a != root_b) {
                p[root_a] = root_b;
                cnt[root_b] += cnt[root_a];
            }
        }

        int ret = 0;
        for (int i = 1; i <= N; i ++ ) ret = max(ret, cnt[i]);

        cout << ret << endl;
    }
    return 0;
}

总结

0.3 + 1 + 0.7 + 0.3 + 1
第一题开始以为是背包，后来发现不对劲，浪费好多时间结果还没搞定
后面时间就很紧了，第三题复盘的时候发现负数的情况没处理，30%应该是死这了
第四题真不会，暴力偷了30%分数
又是一次失败的练习，还得练啊:(

（如果看完了觉得我的解法有问题，或者有更好的解法，欢迎提意见，谢谢~）