树链剖分总结

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

树链剖分总结

作者：

白流雪 , 2022-05-31 19:48:42 , 所有人可见 , 阅读 312

4

4

树链剖分的思想及能解决的问题

树链剖分用于将树分割成若干条链的形式，以维护树上路径的信息
具体来说，将整颗树剖分为若干条链，使它组合成线性结构，然后用其他的数据结构维护信息
树链剖分（树剖/链剖）有多种形式，如重链剖分，长链剖分和用于 $Link/cut \ Tree$ 的剖分（有时被称作“实链剖分”），大多数情况下（没有特别说明时），“树链剖分”都指“重链剖分”。
重链剖分可以将树上的任意一条路径划分成不超过 $O(\log n)$ 条连续的链，每条链上的深度互不相同（也就是不能拐弯）。
重链剖分还能保证划分出的每条链上的节点 $\rm{DFS}$ 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。如：
修改树上两点之间的路径上所有点的值
查询树上两点之间的路径上节点权值的和/极值/其他（在序列上可以用数据结构维护，便于合并的信息）

重链剖分

定义重子节点表示其子节点中子树最大的子节点。如果有多个子树最大的子节点，取其一。如果没有子节点，就无重子节点。定义轻子节点表示剩余的所有子节点。
从一个点到它的重子节点的边为重边。到其他轻子节点的边为轻边。若干条首尾衔接的重边构成重链。
把落单的节点也当做重链，那么整棵树就剖分成若干条重链。

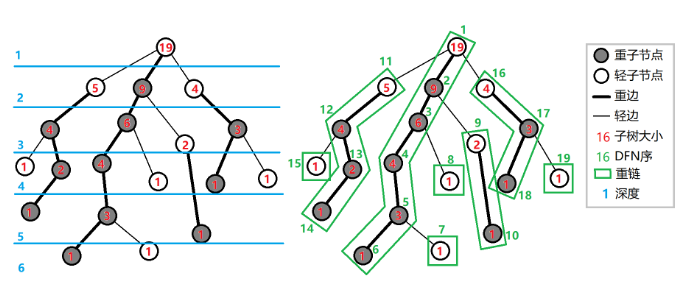
5.31.PNG

重链剖分的性质

树上每个节点都属于且仅属于一条重链
所有的重链将整颗树完全剖分
在剖分时优先遍历重儿子，最后重链的 $\rm{DFS}$ 序就会是连续的
在剖分时重边优先遍历，最后树的 $\rm{DFS}$ 序上，重链内的 $\rm{DFS}$ 序是连续的。按 $\rm{DFS}$ 排序后的序列即为剖分后的链
一颗树内的 $\rm{DFS}$ 序是连续的
可以发现，当我们向下经过一条轻边时，所在子树的大小至少会除以 $2$
因此，对于树上的任意一条路径，把它拆成从 $\rm{LCA}$ 分别向两边向下走，分别最多走 $O(\log n)$ 次，因此，树上的每条路径都可以被拆分成不超过 $O(\log n)$ 条重链
因此，我们成功把树上问题变成了不超过 $O(\log n)$ 条链上的问题，这样可以用数据结构，比如线段树，来维护具体信息，每次操作复杂度 $O(\log^2 n)$

结论：

任何一个点到根的路径上所经过的轻链和重链的数量都是 $O(\log n)$ 级别的。

这个结论等价于，如果我们记 top[x] 表示 $x$ 所属的重链的顶端，fa[x] 表示 $x$ 的父亲，那么我们不断地轮流跳 top[x] 和 fa[x]，只需要跳 $O(\log n)$ 次就可以跳到根。

为什么会这样呢？

因为重链和轻链是交叉的，我们实际上只需要考虑轻链的条数。
我们考虑一条边 $(f, v)$ ，其中 $f$ 是父亲， $v$ 是 $f$ 的轻儿子，我们从 $v$ 跳到了 $f$ 。
为什么 $v$ 是 $f$ 的轻儿子呢？
显然是因为 $f$ 有一个重儿子 $u$ ，明明是它子树更大的，当然 $u$ 才是重儿子而 $v$ 不是了。
这里蕴含着一个大小关系：我们记 size[x] 表示点 $x$ 的子树大小，那么 $\operatorname{size}[u] \geqslant \operatorname{size}[v]$ 。
也就是说，我们从 $v$ 跳到 $f$ 的时候，当前子树大小至少翻了一倍。
换句话说，我们每跳一次轻链，当前子树大小至少翻了一倍。
整个树大小只有 $n$ ，我们最多只能翻倍 $O(\log n)$ 次，因此只能跳 $O(\log n)$ 次轻链。

例题1：树链剖分

如题，已知一颗包含 $N$ 个节点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

1 x y z 表示将树从 $x$ 到 $y$ 节点最短路上所有节点的值都加上 $x$
2 x z 表示将以 $x$ 为根节点的子树内的所有节点值加上 $z$
3 x y 表示求树从 $x$ 到 $y$ 节点最短路径上所有节点的值之和
4 x 表示求以 $x$ 为根节点的子树内所有节点值之和

剖分的过程可以用两遍 $\rm{dfs}$ 实现

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::vector;
using ll = long long;

const int MX = 100005;

vector<int> to[MX];
int n;
int a[MX], fa[MX], dep[MX], son[MX]; // 点权，父节点，深度，重儿子
int top[MX], sz[MX], pre[MX], id[MX], k; // 所在的链头，子树大小，变灰时间，每个时间对应的点，当前时间

int dfs1(int v, int p) {
    fa[v] = p;
    dep[v] = dep[p]+1;
    sz[v] = 1;
    for (int u : to[v]) {
        if (u == p) continue;
        sz[v] += dfs1(u, v);
        if (sz[u] > sz[son[v]]) {
            son[v] = u;
        }
    }
    return sz[v];
}

void dfs2(int v, int t) { // t: 链头
    pre[v] = ++k;
    id[k] = v;
    top[v] = t;
    if (son[v] != 0) dfs2(son[v], t);
    for (int u : to[v]) {
        if (u != fa[v] and u != son[v]) {
            dfs2(u, u);
        }
    }
}

ll sum[MX*4];
ll tag[MX*4];

inline int lc(int x) { return x<<1; }
inline int rc(int x) { return x<<1|1; }

void pushUp(int x) {
    sum[x] = sum[lc(x)] + sum[rc(x)];
}

void moveTag(int p, int l, int r, int t) {
    sum[p] += (r-l+1)*t;
    tag[p] += t;
}

void pushDown(int p, int l, int r) {
    if (tag[p] != 0) {
        int mid = (l+r)/2;
        moveTag(lc(p), l, mid, tag[p]);
        moveTag(rc(p), mid+1, r, tag[p]);
        tag[p] = 0;
    }
}

void buildTree(int p, int l, int r) {
    if (l == r) {
        sum[p] = a[id[l]];
        return;
    }
    int mid = (l+r)/2;
    buildTree(lc(p), l, mid);
    buildTree(rc(p), mid+1, r);
    pushUp(p);
}

void update(int p, int l, int r, int ql, int qr, int d) {
    if (ql <= l and r <= qr) {
        sum[p] += (r-l+1)*d;
        tag[p] += d;
        return;
    }
    int mid = (l+r)/2;
    pushDown(p, l, r);
    if (ql <= mid) {
        update(lc(p), l, mid, ql, qr, d);
    }
    if (mid < qr) {
        update(rc(p), mid+1, r, ql, qr, d);
    }
    pushUp(p);
}

ll query(int p, int l, int r, int ql, int qr) {
    ll res = 0;
    if (ql <= l and r <= qr) {
        return sum[p];
    }
    pushDown(p, l, r);
    int mid = (l+r)/2;
    if (ql <= mid) {
        res += query(lc(p), l, mid, ql, qr);
    }
    if (mid < qr) {
        res += query(rc(p), mid+1, r, ql, qr);
    }
    return res;
}

void updatePath(int u, int v, int d) { // 路径修改 O(log^2)
    while (top[u] != top[v]) { // 循环最多调用 log 次
        if (dep[top[u]] < dep[top[v]]) { // u, v 所在重链的链头谁深就优先处理谁
            std::swap(u, v);
        }
        update(1, 1, n, pre[top[u]], pre[u], d);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) {
        std::swap(u, v);
    }
    update(1, 1, n, pre[v], pre[u], d);
}

ll queryPath(int u, int v) {
    ll res = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) {
            std::swap(u, v);
        }
        res += query(1, 1, n, pre[top[u]], pre[u]);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) {
        std::swap(u, v);
    }
    res += query(1, 1, n, pre[v], pre[u]);
    return res;
}

void updateTree(int u, int d) {
    update(1, 1, n, pre[u], pre[u]+sz[u]-1, d);
}

ll queryTree(int u) {
    return query(1, 1, n, pre[u], pre[u]+sz[u]-1);
}

int main() {
    cin >> n;
    rep(i, n) cin >> a[i];

    rep(i, n-1) {
        int x, y;
        cin >> x >> y;
        to[x].push_back(y);
        to[y].push_back(x);
    }

    dfs1(1, 0);
    dfs2(1, 1);
    buildTree(1, 1, n);

    int q;
    cin >> q;
    rep(qi, q) {
        int type;
        cin >> type;
        if (type == 1) {
            int x, y, z;
            cin >> x >> y >> z;
            updatePath(x, y, z);
        }
        else if (type == 2) {
            int x, z;
            cin >> x >> z;
            updateTree(x, z);
        }
        else if (type == 3) {
            int x, y;
            cin >> x >> y;
            cout << queryPath(x, y) << '\n';
        }
        else {
            int x;
            cin >> x;
            cout << queryTree(x) << '\n';
        }
    }

    return 0;
}

树剖求 LCA

常数比倍增法小一点，可以把两点放在同一条重链上

如果 $(u, v)$ 已经处于同一条重链上，那么显然它们深度更浅的那个一定是 $\operatorname{LCA}$
否则我们取 top[u] 和 top[v] 中深度更深的那个，不妨设为 top[u]，我们让 $u$ 跳到 fa[top[u]]，也就是一次性跳一条重链+一条轻链。
这样操作后，我们可以保证 $u$ 不会跳到 $\operatorname{LCA}$ 的上面，最多只会和 $v$ 跳到同一条重链。
不断进行这两个判断和操作，最终一定会跳到同一条重链上，然后就停止了。

整理一下树链剖分求 $\operatorname{LCA}$ 的过程：

首先预处理每个子树的大小和每个节点的深度，并对每个点选择子树大小最大的儿子作为重儿子，然后顺着重儿子 $\operatorname{dfs}$ ，把重链顶点标记到每个点上。
接着求 $\operatorname{LCA}$ 的时候，就从两个点选 dep[top[x]] 更大的，跳到 fa[top[x]]，直到两个点都在同一条重链上（即 top[x] 相等）
这样我们就在 $O(n)$ 预处理的情况下， $O(\log n)$ 地在线回答了 $\operatorname{LCA}$ 问题，并且常数因子非常小，比倍增小的多。

~~树链剖分是半个 $\log$ 的！~~

例题2：P3379 【模板】最近公共祖先（LCA）

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using std::cin;
using std::cout;
using std::swap;
using std::vector;
using ll = long long;

const int MX = 500005;

vector<int> to[MX];
int n;
int a[MX], fa[MX], dep[MX], son[MX]; // 点权，父节点，深度，重儿子
int top[MX], sz[MX], pre[MX], id[MX], k; // 所在的链头，子树大小，变灰时间，每个时间对应的点，当前时间

int dfs1(int v, int p=0) {
    fa[v] = p;
    dep[v] = dep[p]+1;
    sz[v] = 1;
    for (int u : to[v]) {
        if (u == p) continue;
        sz[v] += dfs1(u, v);
        if (sz[u] > sz[son[v]]) {
            son[v] = u;
        }
    }
    return sz[v];
}

void dfs2(int v, int t) { // t: 链头
    pre[v] = ++k;
    id[k] = v;
    top[v] = t;
    if (son[v] != 0) dfs2(son[v], t);
    for (int u : to[v]) {
        if (u != fa[v] and u != son[v]) {
            dfs2(u, u);
        }
    }
}

int lca(int u, int v) {
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) {
            swap(u, v);
        }
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) {
        return u;
    }
    else {
        return v;
    }
}

int main() {
    int q, s;
    cin >> n >> q >> s;

    rep(i, n-1) {
        int x, y;
        cin >> x >> y;
        to[x].push_back(y);
        to[y].push_back(x);
    }

    dfs1(s);
    dfs2(s, s);

    rep(qi, q) {
        int a, b;
        cin >> a >> b;
        cout << lca(a, b) << '\n';
    }

    return 0;
}

例题：种草

把边权挂在深度较大的那个点上跑一遍树剖即可

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)

using namespace std;
using ll = long long;
using P = pair<int, int>;

const int MX = 100005;

vector<int> g[MX];
int n;
int a[MX], fa[MX], dep[MX], son[MX]; // 点权，父节点，深度，重儿子
int top[MX], sz[MX], pre[MX], id[MX], k; // 所在的链头，子树大小，变灰时间，每个时间对应的点，当前时间

int dfs1(int v, int p) {
    fa[v] = p;
    dep[v] = dep[p]+1;
    sz[v] = 1;
    for (int u : g[v]) {
        if (u == p) continue;
        sz[v] += dfs1(u, v);
        if (sz[u] > sz[son[v]]) {
            son[v] = u;
        }
    }
    return sz[v];
}

void dfs2(int v, int t) { // t: 链头
    pre[v] = ++k;
    id[k] = v;
    top[v] = t;
    if (son[v] != 0) dfs2(son[v], t);
    for (int u : g[v]) {
        if (u != fa[v] and u != son[v]) {
            dfs2(u, u);
        }
    }
}

ll sum[MX*4];
ll tag[MX*4];

inline int lc(int x) { return x<<1; }
inline int rc(int x) { return x<<1|1; }

void pushUp(int x) {
    sum[x] = sum[lc(x)] + sum[rc(x)];
}

void moveTag(int p, int l, int r, int t) {
    sum[p] += (r-l+1)*t;
    tag[p] += t;
}

void pushDown(int p, int l, int r) {
    if (tag[p] != 0) {
        int mid = (l+r)/2;
        moveTag(lc(p), l, mid, tag[p]);
        moveTag(rc(p), mid+1, r, tag[p]);
        tag[p] = 0;
    }
}

void buildTree(int p, int l, int r) {
    if (l == r) {
        sum[p] = a[id[l]];
        return;
    }
    int mid = (l+r)/2;
    buildTree(lc(p), l, mid);
    buildTree(rc(p), mid+1, r);
    pushUp(p);
}

void update(int p, int l, int r, int ql, int qr, int d) {
    if (ql <= l and r <= qr) {
        sum[p] += (r-l+1)*d;
        tag[p] += d;
        return;
    }
    int mid = (l+r)/2;
    pushDown(p, l, r);
    if (ql <= mid) {
        update(lc(p), l, mid, ql, qr, d);
    }
    if (mid < qr) {
        update(rc(p), mid+1, r, ql, qr, d);
    }
    pushUp(p);
}

ll query(int p, int l, int r, int ql, int qr) {
    ll res = 0;
    if (ql <= l and r <= qr) {
        return sum[p];
    }
    pushDown(p, l, r);
    int mid = (l+r)/2;
    if (ql <= mid) {
        res += query(lc(p), l, mid, ql, qr);
    }
    if (mid < qr) {
        res += query(rc(p), mid+1, r, ql, qr);
    }
    return res;
}

void updatePath(int u, int v, int d=1) { // 路径修改 O(log^2)
    while (top[u] != top[v]) { // 循环最多调用 log 次
        if (dep[top[u]] < dep[top[v]]) { // u, v 所在重链的链头谁深就优先处理谁
            std::swap(u, v);
        }
        update(1, 1, n, pre[top[u]], pre[u], d);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) {
        std::swap(u, v);
    }
    update(1, 1, n, pre[v]+1, pre[u], d);
}

ll queryPath(int u, int v) {
    ll res = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) {
            swap(u, v);
        }
        res += query(1, 1, n, pre[top[u]], pre[u]);
        u = fa[top[u]];
    }
    if (dep[u] < dep[v]) {
        swap(u, v);
    }
    res += query(1, 1, n, pre[v]+1, pre[u]);
    return res;
}

int main() {
    int m;
    cin >> n >> m;

    rep(i, n-1) {
        int x, y;
        cin >> x >> y;
        g[x].push_back(y);
        g[y].push_back(x);
    }

    dfs1(1, 0);
    dfs2(1, 1);
    buildTree(1, 1, n);

    rep(i, m) {
        char type;
        int x, y;
        cin >> type >> x >> y;
        if (type == 'P') {
            updatePath(x, y);
        }
        else {
            cout << queryPath(x, y) << '\n';
        }
    }

    return 0;
}

3 评论

Gzm1317 2022-05-31 21:14

谢谢爹爹

Hanasaki 2022-05-31 20:44

感谢大神总结Orz

shiye 2022-05-31 20:35

mark一个

App 内打开