高斯消元解线性方程组

作者： 作者的头像   009JEAN ,  2022-05-30 20:36:50 ,  所有人可见 ,  阅读 220

0


高斯消元解线性方程组

原题链接：883. 高斯消元解线性方程组 - AcWing题库

解题思路

我们可以把这样一个方程组的系数表示成矩阵的形式

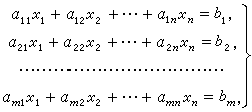
9a504fc2d5628535be9dcb5f90ef76c6a7ef634a.gif

用题目中的样例举例子：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

可以表示为：

i = 0 i = 1 i = 2 i = 3
j = 0 1.00 2.00 -1.00 -6.00
j = 1 2.00 1.00 -3.00 -9.00
j = 2 -1.00 -1.00 2.00 7.00

接下来我们可以利用矩阵初等行列变换的三种操作：

1、把某一行乘以一个非零的数

2、交换某两行

3、把某行的若干倍加到另一行上去

把某一行把矩阵变成上三角形式（最简阶梯型等式）

i = 0 i = 1 … i = n-1 i = n
j = 0 a11*x1 a12*x2 … a1n*xn b1
j = 1 0 a22*x2 … a2n*xn b2
… … … … … …
j = n 0 0 … ann*xn bn

通过这个形式我们就可以从第n行一行一行往上求解b

化简上成三角形式

枚举每一列

1、找到绝对值最大的一行

这样可以保证浮点数的精度

在样例中第一列绝对值最大的是2.00

[i = 0] i = 1 i = 2 i = 3
j = 0 1.00 2.00 -1.00 -6.00
[j = 1] [2.00] 1.00 -3.00 -9.00
j = 2 -1.00 -1.00 2.00 7.00 
for(int j = r;j < n;j ++)
{
    if(fabs(a[j][i]) > fabs(a[big][i]))big = j;
}

2、将改行换到最上面（未确定或者说经过操作的行（i < r）在的最上面）

[i = 0] i = 1 i = 2 i = 3
[j = 0] 2.00 1.00 -3.00 -9.00
[j = 1] 1.00 2.00 -1.00 -6.00
j = 2 -1.00 -1.00 2.00 7.00 
for(int j = i;j <= n;j ++)swap(a[big][j],a[r][j]);

3、将该行的第一个数变成1

我们可以把这行都除以第一个数

样例中这行的第一个数是2就除以2

[i = 0] i = 1 i = 2 i = 3
[j = 0] 1.00 0.50 -1.50 -4.50
j = 1 1.00 2.00 -1.00 -6.00
j = 2 -1.00 -1.00 2.00 7.00 
for(int j = n;j >= i;j --)a[r][j] /= a[r][i];

4、把下面的几行行的这一列削成0

这样就可以构造正三角

我们把其他几行减去这一行乘对应的倍数

[i = 0] i = 1 i = 2 i = 3
[j = 0] 1.00 0.50 -1.50 -4.50
j = 1 0.00 1.50 0.50 -1.50
j = 2 0.00 -0.50 0.50 2.50 
for(int j = r + 1;j < n;j ++)
{
    if(fabs(a[j][i]) > zero)
    {
        for(int k = n;k >= i;k --)a[j][k] -= a[r][k] * a[j][i];
    }
}

然后继续下一个循环

最终求解

如果化简之后是阶梯型说明有唯一解：

就可以从第n行一行一行往上求解b

如果不是就说明没有唯一解：

说明等式中有几行是0 = ?的

如果有0 = 非零数矛盾了就是无解

如果没有0 = 非零数就说明有几行是0 = 0可以被多种方式表达就是有无数多组解

if(r < n)//判断非唯一解情况
{
    for(int j = r;j < n;j ++)
    {
        if(fabs(a[j][n]) > zero)return 1;//1表示无解
    }
    return 0;//0表示无数解
}

for(int x = n - 1;x >= 0;x --)//遍历上三角，求解方程
{
    for(int y = x + 1;y < n;y ++)
    {
        a[x][n] -= a[x][y] * a[y][n];
    }
}

return 2;//2表示唯一解

源代码

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>

using namespace std;

const int N = 110;
const double zero = 1e-6;//浮点有误差，不能直接判断是不是等于零

int n;
double a[N][N];

int func()//构造上三角，判断无数解，唯一解和无解
{
    int i = 0;//i是遍历到的列
    int r = 0;//r是已经确定的行
    for(;i < n;i ++)
    {
        int big = r;//big是绝对值最大的数所在的行数
        for(int j = r;j < n;j ++)
        {
            if(fabs(a[j][i]) > fabs(a[big][i]))big = j;
        }

        if(fabs(a[big][i]) < zero)
        {
            continue;
        }

        for(int j = i;j <= n;j ++)swap(a[big][j],a[r][j]);
        for(int j = n;j >= i;j --)a[r][j] /= a[r][i];
        for(int j = r + 1;j < n;j ++)
        {
            if(fabs(a[j][i]) > zero)
            {
                for(int k = n;k >= i;k --)a[j][k] -= a[r][k] * a[j][i];
            }
        }

        r ++;
    }


    if(r < n)//判断非唯一解情况
    {
        for(int j = r;j < n;j ++)
        {
            if(fabs(a[j][n]) > zero)return 1;//1表示无解
        }
        return 0;//0表示无数解
    }

    for(int x = n - 1;x >= 0;x --)//遍历上三角，求解方程
    {
        for(int y = x + 1;y < n;y ++)
        {
            a[x][n] -= a[x][y] * a[y][n];
        }
    }

    return 2;//2表示唯一解
}

int main()
{
    scanf("%d",&n);

    for(int i = 0;i < n;i ++)
    {
        for(int j = 0;j < n + 1;j++)
        {
            cin >> a[i][j];
        }
    }    

    int re_1 = func();
    if(re_1 == 0)puts("Infinite group solutions");
    else if(re_1 == 1)puts("No solution");
    else 
    {
        for(int i = 0;i < n;i ++)
        {
            if(fabs(a[i][n]) == 0)//防止-0.00
            {
                puts("0.00");
                continue;
            }
            printf("%.2f\n",a[i][n]);
        }
    }

    return 0;
}

0 评论

1024
x