1. 中序遍历

中序遍历过程的顺序是 左 -> 根 -> 右

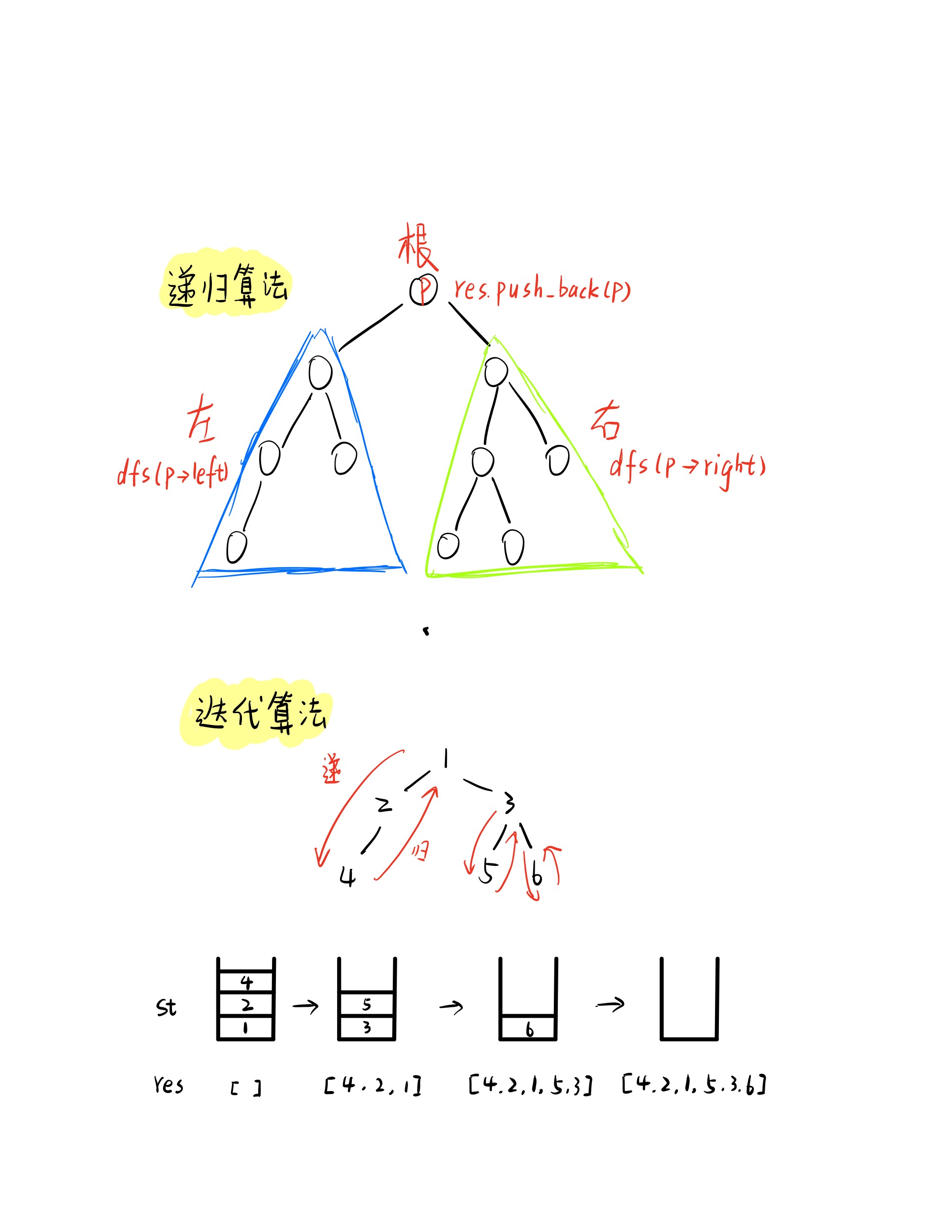
递归算法

递归算法比较简单，就根据中序遍历的过程，先遍历左子树，再遍历当前根，然后遍历右子树。递归函数的中止条件是当前结点为空，同时当遍历当前结点时，将该点加入遍历数组即可。

调用递归函数时可以看作它已经帮你完成了你所想要完成的所有事，它已经将答案封装好交到了你的手上。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> res;
    vector<int> inorderTraversal(TreeNode* root) {
        dfs(root);
        return res;
    }

    void dfs(TreeNode* root)
    {
        if (!root) return;
        dfs(root -> left);
        res.push_back(root -> val);
        dfs(root -> right);
    }
};

迭代算法

递归函数实现的过程其实就是系统帮我们调用栈的过程，所以如果换为迭代算法来写，我们只需要自己模拟实现一个栈。

递归的实现也可以反映成一棵树，就是所谓的递归树，当我们调用递归函数的时候，其实有两个过程，一个是向下的递的过程，然后再是向上的归的过程。递归函数很好地封装了这一点，然而当我们用迭代算法时，需要自己去模拟递和归的过程。

遍历是，我们需要将所有左子树链上的所有点放入栈中，该过程即为递,然后取出栈顶，加入遍历数组，之后再放入右子树，同时注意这里的右子树指的是整个右子树的左子树链。直到遍历完所有结点。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> st;

        auto p = root;

        while (p || !st.empty())
        {
            while (p)
            {
                st.push(p);
                p = p -> left;
            }

            p = st.top();
            st.pop();
            res.push_back(p -> val);
            p = p -> right;
        }

        return res;
    }
};

2. 前序遍历

前序遍历顺序为根 -> 左 -> 右，所以运用递归算法时，先将该点放入遍历数组，再递归遍历左子树和右子树

递归算法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> res;
    vector<int> preorderTraversal(TreeNode* root) {
        dfs(root);
        return res;
    }

    void dfs(TreeNode* root)
    {
        if (!root) return;
        res.push_back(root -> val);
        dfs(root -> left);
        dfs(root -> right);
    }
};

迭代算法

当前遍历结点即为根，所以在迭代算法中，先将该点放入遍历数组，然后将左子树链递到最低层，然后出栈，放入右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> st;
        auto p = root;

        while (p || !st.empty())
        {
            while (p)
            {
                res.push_back(p -> val);
                st.push(p);
                p = p -> left;
            }

            p = st.top();
            st.pop();
            p = p-> right;
        }

        return res;
    }
};

3. 后序遍历

后序遍历的顺序为左 -> 右 -> 根

根据观察，后序遍历倒过来的顺序为根 -> 右 -> 左

而我们已经知道如何进行先序遍历根 -> 左 -> 右

在递归算法中比较好些，只需要调整遍历顺序。但是在迭代算法中，我们首先需要先模拟先序遍历的过程，同时将先序遍历中左右子树遍历过程对换，最后还需将遍历数组翻转才可以得到后序遍历。

递归算法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> res;
    vector<int> postorderTraversal(TreeNode* root) {
        dfs(root);
        return res;
    }

    void dfs(TreeNode* root)
    {
        if (!root) return;
        dfs(root -> left);
        dfs(root -> right);
        res.push_back(root -> val);
    }
};

迭代算法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> st;

        auto p = root;
        while (p || !st.empty())
        {
            while (p)
            {
                res.push_back(p -> val);
                st.push(p);
                p = p -> right;
            }

            p = st.top();
            st.pop();
            p = p -> left;
        }
        reverse(res.begin(), res.end());
        return res;
    }
};

4. 层次遍历

算法思路

层序遍历，顾名思义需要对二叉树进行一层一层的遍历。因此可以采用BFS的思路，根据BFS的性质，每进行一次扩展，会将下一层的点全部放入队列中，所以每次在对队列进行取出操作时，当前队列中的所有元素均当前层元素。因为我们需要一边取出元素，一边放入元素。所以在每一次更迭前，先记录当前的队列的大小，即为当前层的元素，然后取出队头的该几个元素，放入当前层遍历数组level中，同时对左右儿子进行扩展。每遍历完一层，最后将level数组插入最终遍历数组中。

C ++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if (!root) return res;

        queue<TreeNode*> q;
        q.push(root);

        while (q.size())
        {
            int n = q.size();
            vector<int> level;

            for (int i = 0; i < n; i ++)
            {
                auto t = q.front();
                q.pop();
                level.push_back(t -> val);
                if (t -> left) q.push(t -> left);
                if (t -> right) q.push(t -> right);
            }

            res.push_back(level);
        }

        return res;
    }
};