初见安~欢迎到原博客地址食用： 专题·LCA

LCA——最近公共祖先，即在一棵树上任意两点向根节点靠近的路上重合的深度最深的点。【自己的理解，可能不准确】

就比如下面这棵树：

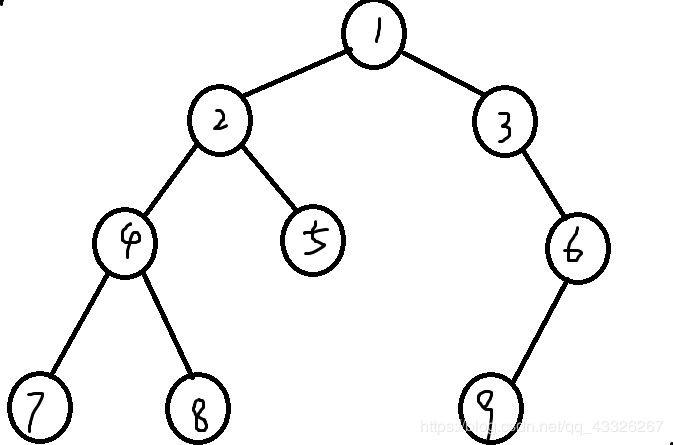
节点4和6的最近公共祖先是点1，节点7和5的最近公共祖先是点2。

【后文三种解法题目均为：洛谷P3379 【模板】最近公共祖先】 】

LCA的用处不少，所以掌握求LCA的方法也是很重要的。如下【本人只会三种】有三种解法：

1.倍增法

我们首先脑补一下求LCA的过程——两个节点平层同时往上跳，直到相遇，相遇的点就是他们的LCA。但是很明显，如果这棵树的深度较大，那么就要跳很久了【这是最最朴素的做法，复杂付O(n*m)】。所以可以采用倍增优化——大步大步地跳。

我们首先要记录下每个节点的父节点和各个祖先借点，可以开一个fa[maxn][25]，fa[x][i]表示节点x的第i+1位祖先，也就是说x的父亲节点就是fa[x][0]，爷爷就是fa[x][1]亦是父亲的父亲fa[fa[x][0]][0]……以此类推，这样在更新的时候我们就可以得到一个递推式：fa[x][i] = fa[fa[x][i - 1]][i - 1].就可以预处理出每个节点的各个祖先。

再者就是——大步大步跳，跳多少呢？明显是（dep为节点深度）。每一次都log一下还要换底（log函数默认底数为e），所以log我们也打表预处理出来。

在向上跳时，我们先让x和y处于同一层，让深度更深的一个先往上跳，然后两个再一起跳，直到两点有了同一个父亲。当然，在刚刚得到两点平层的时候可以特判一下：是否两点已经汇合了，是则可以返回了。

以上是思路，下面上代码及详解——

#include<bits/stdc++.h>
#define maxn 500005
using namespace std;
int n, m, root;
int read()
{
    int x = 0, f = 1, ch = getchar();
    while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();};
    while(isdigit(ch)) x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
    return x * f;
}

struct edge
{
    int to, nxt;
    edge() {}
    edge(int tt, int nn) {to = tt, nxt = nn;}
}e[maxn << 1];

int head[maxn], k = 0;
void add(int u, int v)
{
    e[k] = edge(v, head[u]);
    head[u] = k++;
}

int fa[maxn][25], dep[maxn], lg[maxn];
void dfs(int now, int fath)//初始化深度及祖祖辈辈
{
    dep[now] = dep[fath] + 1;
    fa[now][0] = fath;
    for(int i = 1; (1 << i) <= dep[now]; i++)
        fa[now][i] = fa[fa[now][i - 1]][i - 1];//前文的递推式

    for(int i = head[now]; ~i; i = e[i].nxt)
        if(e[i].to != fath) dfs(e[i].to, now);//继续往下遍历
}

int lca(int x, int y)
{
    if(dep[x] < dep[y]) swap(x, y);//保证x的深度更大，跳x
    while(dep[x] > dep[y]) x = fa[x][lg[dep[x] - dep[y]] - 1];
    if(x == y) return x;//特判
    for(int i = lg[dep[x]]; i >= 0; i--)//倍增一起往上跳
        if(fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];

    return fa[x][0];
}

int main()
{
    memset(head, -1, sizeof head);
    n = read(), m = read(), root = read();
    register int u, v;
    for(int i = 1; i < n; i++)
    {
        u = read(), v = read();
        add(u, v);
        add(v, u);
    }

    dfs(root, 0);
    for(int i = 1; i <= n; i++)
        lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);//log打表，后面那一坨是特判一下i是否进位了
    for(int i = 1; i <= m; i++)
    {
        u = read(), v = read();
        printf("%d\n", lca(u, v));
    }
    return 0;
}

最后测出来跑了1300+ms，讲真还是比较慢了，毕竟倍增也可以在跳多少这种问题上徘徊很久。复杂度大约是O（mlogn）。

2.Tarjan

前面的倍增很明显，是强制在线算法，必须针对每一个问题单独去操作一次。而Tarjan则恰恰相反，是强制离线算法。

大致思路是这样的：先很自然地深优遍历下去，如果当前节点x涉及到某一个询问且询问的另一个点已经访问过了，那么就可以得出答案了；反之标记点x已经访问过，直到访问到另一个节点。可能比较抽象，我们抽象地看图理解一下这个思路：

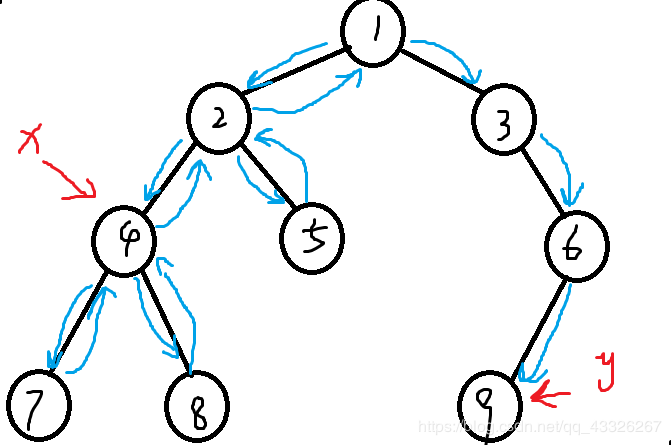
假设询问为点4和9，我们从根节点出发，访问到了x，标记访问过了；发现9并没有被访问到，所以不管，继续走；回溯，遍历，当遇到9的时候，发现另一个点4已经访问过了，所以此时两个点的LCA就是更新到了的4的祖先，节点1。

你可能会问——从1开始遍历，不本来就是每个点的祖先都是1么？那么如果我们在回溯的时候才更新呢？我们设fa[maxn]，fa[x]为点x的祖先节点，用法同并查集。如图，也就是说我们从：1->2->4->7，到了叶子节点了，开始回溯，标记fa[7] = 4；再遍历，到8，回溯，标记fa[8] = 4；再回，b标记fa[4] = 2；下走，至5，回溯，标记fa[5] = 2……也就是说随着回溯的当前层的深度越来越浅，各个节点最终指向的祖先也越来越高。所以说在当前思路下，发现另一个点已经标记了，那么那个点的祖先就一定是两个点的LCA。

同时，在访问到一个点时，我们可以一并解决所有与这个点有关的询问，所以我们的询问也要用邻接表来存贮。当然用vector也可以的。这就是问什么Tarjan强制离线。

下面是代码及详解——

#include<bits/stdc++.h>
#define maxn 500005
using namespace std;
int n, m, root, lca[maxn << 1];
int read()
{
    int x = 0, f = 1, ch = getchar();
    while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
    while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
    return x * f;
}

struct edge
{
    int to, nxt;
    edge(){}
    edge(int tt, int nn) {to = tt, nxt = nn;}
}e[maxn << 1], qe[maxn << 1];

int head[maxn], k = 0;
void add(int u, int v)
{
    e[k] = edge(v, head[u]);
    head[u] = k++;
}

int qhead[maxn], qk = 0;
void qadd(int u, int v)
{
    qe[qk] = edge(v, qhead[u]);
    qhead[u] = qk++;
}

int fa[maxn];
int get(int x) {return fa[x] == x? x : fa[x] = get(fa[x]);}//记得路径压缩！！

bool vis[maxn];
void tarjan(int u)
{
    register int v;
    vis[u] = 1;
    for(int i = head[u]; ~i; i = e[i].nxt)//先深优遍历下去
    {
        v = e[i].to;
        if(vis[v]) continue;//vis过了，就说明是父亲
        tarjan(v);
        fa[v] = u;//回溯时记录
    }

    for(int i = qhead[u]; ~i; i = qe[i].nxt)//开始扫一遍关于u的所有询问
    {
        v = qe[i].to;
        if(vis[v])//另一个点访问过了，可以得出答案了
        {
            lca[i] = get(v);
            if(i & 1) lca[i - 1] = lca[i];//这里特殊处理是因为每个询问存了两次
            else lca[i + 1] = lca[i];
        }
    }
}

int main()
{
    memset(head, -1, sizeof head);
    memset(qhead, -1, sizeof qhead);
    n = read(), m = read(), root = read();
    register int u, v;
    for(int i = 1; i < n; i++)
    {
        u = read(), v = read();
        add(u, v);
        add(v, u);
        fa[i] = i;//顺便初始化fa
    }

    fa[n] = n;
    for(int i = 1; i <= m; i++)
    {
        u = read(), v = read();//存储询问
        qadd(u, v);
        qadd(v, u);
    }

    tarjan(root);//开始遍历

    for(int i = 0; i < m; i++)
        printf("%d\n", lca[i << 1]);//每个询问都存了两次，所以要*2
}

Tarjan最后耗时是900+ms，少了很多，大概时间复杂度为O(n+m)，也就是说在m很小的时候用倍增更优，在m较大的时候用Tarjan更优。毕竟若是有说一种比另一种绝对更优的话，就不会同时存在了。

3.树剖解法

首先树剖入门一下：传送门：树链剖分

我们知道树剖是把一棵树按子树大小分为链。树剖基本操作中有一个是求x到y的路径的边权和，或者是所有边权进行修改。那就很明显了——我们可以用树剖的思路来写LCA！！！直接看点x和y是否在一条链上，不在则深度较大者跳到链头的父亲节点处，也就是跳出这条链；在则深度较浅者为LCA。

树剖的话很明显——一跳就是一条链，对于n极大的情况就相当于是倍增的再一优化。最后这份代码跑出来是1100+ms。尽管还是比Tarjan慢，但是一定是比倍增优的，而且相比之下思路也要简单很多！！！

#include<bits/stdc++.h>//都是树剖模板操作，就不做多解释了。
#define maxn 500005
using namespace std;
int n, m, root;
int read()
{
    int x = 0, f = 1, ch = getchar();
    while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
    while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
    return x * f;
}
struct edge
{
    int to, nxt;
    edge(){}
    edge(int tt, int nn)
    {
        to = tt, nxt = nn;
    }
}e[maxn << 1];

int k = 0, head[maxn];
void add(int u, int v)
{
    e[k] = edge(v, head[u]);
    head[u] = k++;
}

int fa[maxn], dep[maxn], size[maxn], son[maxn];
void dfs_getson(int u)
{
    size[u] = 1;
    for(int i = head[u]; ~i; i = e[i].nxt)
    {
        int v = e[i].to;
        if(v == fa[u]) continue;
        dep[v] = dep[u] + 1;
        fa[v] = u;
        dfs_getson(v);
        size[u] += size[v];
        if(size[v] > size[son[u]]) son[u] = v;
    }
}

int top[maxn];
void dfs_rewrite(int u, int tp)
{
    top[u] = tp;
    if(son[u]) dfs_rewrite(son[u], tp);
    for(int i = head[u]; ~i; i = e[i].nxt)
    {
        int v = e[i].to;
        if(v != fa[u] && v != son[u]) dfs_rewrite(v, v);
    }
}

void ask(int x, int y)
{
    while(top[x] != top[y])//不同则跳
    {
        if(dep[top[x]] > dep[top[y]]) swap(x, y);
        y = fa[top[y]];
    }
    if(dep[x] > dep[y]) swap(x, y);
    printf("%d\n", x);//输出深度较小者
}

int main()
{
    memset(head, -1, sizeof head);
    n = read(), m = read(), root = read();
    int u, v;
    for(int i = 1; i < n; i++)
    {
        u = read(), v = read();
        add(u, v);
        add(v, u);
    }
    //树剖初始化
    dfs_getson(root);
    dfs_rewrite(root, root);

    for(int i = 1; i <= m; i++)
    {
        u = read(), v = read();
        ask(u, v);
    }
    return 0;
}

作为一个第一次接触LCA竟然是用树剖过的的人表示终于整理完了！！！

迎评：）
——End——