0. 集合角度看DP问题

1. 集合划分的原则：不重不漏
2. 划分的依据：最后一个不同的状态

1. 数字三角形模型

摘花生

$O(n^2)$

$$DP \begin{cases} 状态表示f[i, j] \begin{cases} 集合：所有从点(1, 1)走到点(i, j)的路线 \\\\ 属性：\fbox{Max}/Min/数量 \\\\ \end{cases} \\\\ \\\\ 状态计算-集合的划分 \begin{cases} 1. 最后一步从上面下来 \to f[i - 1, j] + w[i, j] \\\\ 2. 最后一步从左边过来 \to f[i, j - 1] + w[i, j] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

最低通行费

$O(n^2)$

$$DP \begin{cases} 状态表示f[i, j] \begin{cases} 集合：所有从点(1, 1)走到点(i, j)的路线 \\\\ 属性：Max/\fbox{Min}/数量 \\\\ \end{cases} \\\\ \\\\ 状态计算-集合的划分 \begin{cases} 1. 最后一步从上面下来 \to f[i - 1, j] + w[i, j] \\\\ 2. 最后一步从左边过来 \to f[i, j - 1] + w[i, j] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

方格取数

$O(n^3)$
走两次：$f[i1, j1, i2, j2]$表示所有从(1, 1), (1, 1)分别走到(i1, j1), (i2, j2)的路径的最大值
处理同一个格子不能被重复选择的问题
当且仅当$i1 + j1 = i2 + j2$时，两条路径的格子才可能重合
k表示两条路线当前走到的格子的横纵坐标之和

$$DP \begin{cases} 状态表示f[k, i1, i2] \begin{cases} 集合：表示所有从(1, 1), (1, 1)分别走到(i1, k - i1), (i2, k - i2)\\\\ 的所有路径 \\\\ 属性：\fbox{Max}/Min/数量 \\\\ \end{cases} \\\\ \\\\ 状态计算-看最后一步 \begin{cases} 1. 第一条和第二条路径都从上面下来 \\\\ 2. 第一条和第二条路径都从左边过来 \\\\ 3. 一上，二左 \to f[k - 1, i1 - 1, i2] \begin{cases} 重合：w[i1, j1] \\\\ 不重合：w[i1, j1] + w[i2, j2] \\\\ \end{cases} \\\\ \\\\ 4. 一左，二上 \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

传纸条

$O(n^3)$
与方格取数不同的是，除了开始和结束节点，两条路径不允许走相同的节点

2. 最长上升子序列模型（LIS）

怪盗基德的滑翔翼

$O(n^2)$

1. 只能选一个方向且中途不能改变方向
2. 从左往右做一遍LIS，再从右往左做一遍LIS
3. 答案取最大值

合唱队形 & 登山

$O(n^2)$

1. 按照编号递增的顺序浏览
2. 相邻两个景点（同学）的高度不能相同
3. 一旦开始下降，就不能上升
4. 求最多能浏览多少景点（最多能有多少个同学能留在合唱队里）
5. 预处理出以每个点结尾的最长上升子序列和以每个点开始的最长下降子序列

友好城市

$O(n^2)$

1. 每个城市上只能建立一座桥
2. 桥间不能相交
3. 最多可以建多少桥
4. 两岸的桥不相交，等价于将一端城市排序后，桥的另一端对应的城市也应该是有序的，否则就会有交叉
5. 于是问题转化为求另一端最长有序子序列是多少

最大上升子序和

$O(n^2)$

$$DP \begin{cases} 状态表示f[i] \begin{cases} 集合：表示所有以a[i]结尾的上升子序列 \\\\ 属性：和的最大值 \\\\ \end{cases} \\\\ \\\\ 状态计算-看倒数第2个数 \begin{cases} 1. 倒数第2个数不存在 \to a[i] \\\\ 2. 倒数第2个数是a[1] \to f[1] + a[i] \\\\ 3. 倒数第2个数是a[2] \to f[2] + a[i] \\\\ 4. \cdots \\\\ i. 倒数第2个数是a[i - 1] \to f[i - 1] + a[i] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

拦截导弹

$O(n^2)$

1. 第一问：求最长下降子序列
2. 第二问：贪心流程，从前往后扫描每个数，对于每个数：
   • 情况1：如果现有的子序列的结尾都小于当前数，则创建新子序列；
   • 情况2：将当前数放到结尾大于等于它的最小的子序列后面。
3. 证明贪心法得到的解和最优解相等：A表示贪心算法得到的序列个数；B表示最优解。显然$A \geq B$；然后使用调整法说明$A \leq B$，假设最优解对应的方案数和贪心方案数不同，即当前扫描到的数为$x$，最优解方案中$x$应该放到子序列$l_1$的结尾$b$，而贪心方案中$x$应该放到子序列$l_2$的结尾$a$（$l_1$和$l_2$是子序列集合中的两个不同子序列），于是有$b \geq a$，那么交换两个方案中$x$之后的序列并不会增加子序列的个数，也就是最优解经过某种调整方式一定能变成贪心解，而且还不会使得答案的值变大，即$B \geq A$，综上有$A = B$，这种贪心思路与贪心解法的最长上升子序列是一样的，问题就转变为求最长上升子序列。

导弹防御系统

1. 数列中的每个值要么属于某个上升子序列，要么属于某个下降子序列
2. 最少需要多少个上升和下降子序列能把整个数列完全覆盖
   参考 题解1, 题解2

最长公共上升子序列

$$DP \begin{cases} 状态表示f[i, j] \begin{cases} 集合：表示所有由第一个序列前i个字母和第二个序列前j个字母构成的，\\\\ 且以b[j]结尾的公共上升子序列 \\\\ 属性：Max \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 1. 所有包含a[i]的公共上升子序列 \\\\ 根据数列b划分所有情况 \begin{cases} 1. 倒数第2个数不存在 \to 1 \\\\ 2. 倒数第2个数是b[1] \to f[i, 1] \\\\ 3. 倒数第2个数是b[2] \to f[i, 2] \\\\ 4. \cdots \\\\ j. 倒数第2个数是b[j - 1] \to f[i, j - 1] \\\\ \end{cases} \\\\ 2. 所有不包含a[i]的公共上升子序列 \to f[i - 1, j] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

3. 背包模型

组合类DP，不考虑相邻两个数之间的关系，只考虑全局的信息（相比于序列DP）

不同背包模型之间状态表示都是一样的，区别在于状态的划分

$$01背包 \begin{cases} 状态表示f[i, j] \begin{cases} 集合：所有只从前i个物品中选，且总体积不超过j的选法的集合 \\\\ 属性：Max（最大价值？）/Min（最小重量？）/数量（求方案数？） \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 1. 不选第i个物品的所有方案 \to f[i - 1, j] \\\\ 2. 选第i个物品的所有方案 \to f[i - 1, j - v_i] + w_i \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

$$完全背包的状态划分 \begin{cases} 不选第i个物品的所有方案 \to f[i - 1, j] \\\\ 第i个物品选1个的所有方案 \to f[i - 1, j - v_i] + w_i \\\\ 第i个物品选2个的所有方案 \to f[i - 1, j - 2 \ast v_i] + 2 \ast w_i \\\\ \cdots \\\\ 第i个物品选s个的所有方案 \to f[i - 1, j - s \ast v_i] + s \ast w_i \\\\ \end{cases} \\\\ $$

$$分组背包 \begin{cases} 状态表示f[i, j] \begin{cases} 集合：所有只从前i组物品中选，且总体积不超过j的选法的集合 \\\\ 属性：Max/Min/Count \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 1. 不选第i组物品的所有方案 \to f[i - 1, j] \\\\ 2. 选第i组物品中的第k个物品所有方案 \to f[i - 1, j - v[i, k]] + w[i, k] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

数字组合

$$DP \begin{cases} 状态表示f[i, j] \begin{cases} 集合：表示所有只从前i个物品中选，且总体积\fbox{恰好}是j的方案的集合 \\\\ 属性：Count \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 不包括物品i的所有选法 \to f[i - 1, j] \\\\ 包括物品i的所有选法 \to f[i - 1, j - v_i] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

$$状态转移方程：f[i, j] = f[i - 1, j] + f[i - 1, j - v_i]$$

潜水员

$$DP \begin{cases} 状态表示f[i, j, k] \begin{cases} 集合：表示所有从前i个物品中选，且氧气含量\fbox{至少}是j，\\\\ 氮气含量\fbox{至少}是k的所有选法 \\\\ 属性：Min \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 不包括物品i的所有选法 \to f[i - 1, j, k] \\\\ 包括物品i的所有选法 \to f[i - 1, j - v_{i1}, k - v_{i2}] + w_i \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

$$一些区别 \begin{cases} 1. 体积最多是j：f[i] = 0, V \geq 0 \\\\ 2. 体积恰好是j：f[0] = 0, f[i] = +\infty, V \geq 0 \\\\ 3. 体积至少是j：f[0] = 0, f[i] = +\infty, V可以小于0 \\\\ \end{cases}$$

背包问题求具体方案

先把答案求出来再反着推

$判断每个物品是否被选 \begin{cases} 1. 只能选物品i，则必选物品i \\\\ 2. 只能不选物品i，则必不选物品i \\\\ 3. 可选也可不选物品i，则必选物品i（选的字典序比不选的小） \\\\ \end{cases}$

货币系统

【性质1】：$a_1, a_2, \cdots, a_n$一定都可以被$b$表示出来
【性质2】：在最优解中，$b_1, b_2, \cdots, b_m$一定都是从$a_1, a_2, \cdots, a_n$中选择的

说明：若存在$b_k$不属于集合$A$，则它能被表示为$a_1, a_2, \cdots, a_n$的线性组合，又因为$a_i$可以被$b_i$的线性组合表示出来，那么也能被$b_i$的线性组合表示出来，所以$b_k$是多余的。

【性质3】：$b_1, b_2, \cdots, b_m$一定不能被其他$b_i$表示出来

有依赖的背包问题

$$DP \begin{cases} 状态表示f[u, j] \begin{cases} 集合：所有从以u为根的子树中选，且总体积不超过j的方案 \\\\ 属性：Max \\\\ \end{cases} \\\\ \\\\ 状态计算（为每棵子树分别分配多少体积使总体积不超过j时价值最大） \begin{cases} 子树1 \\\\ 子树2 \\\\ \cdots \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

能量石

1. 不同石头每秒损失的能量不同，因此相同的一批石头按照不同顺序吃获得的能量不同
2. 如果暴力枚举石头顺序，那么$n$个石头有$n!$种排列，超时
3. 通过寻找最优解下石头被吃顺序的性质缩小枚举空间，若存在两个石头被吃的顺序不满足性质，则交换吃的顺序
4. 确定石头被吃的顺序后，即可按01背包的思路枚举每个石头吃或者不吃求最大能量

说明：对于石头序列中的两个石头$Stone_i(S_i, E_i, L_i)$和$Stone_{i + 1}(S_{i + 1}, E_{i + 1}, L_{i + 1})$，假设已经过了$t$个时间，现在要选择先吃$Stone_i$还是$Stone_{i + 1}$，那么
$$先吃Stone_i获得的能量为：\epsilon_{i} = \Delta E_{before} + \overbrace{E_i - t \ast L_i}^{\Delta E_i} + \overbrace{E_{i + 1} - (t + S_i) \ast L_{i + 1}}^{\Delta E_{i + 1}} \\\\ 先吃Stone_{i + 1}获得的能量为：\epsilon_{i + 1} = \Delta E_{before} + \overbrace{E_{i + 1} - t \ast L_{i + 1}}^{\Delta E_{i + 1}} + \overbrace{E_i - (t + S_{i + 1}) \ast L_i}^{\Delta E_i} \\\\ \epsilon_{i} > \epsilon_{i + 1} \implies \frac{S_i}{L_i} < \frac{S_{i + 1}}{L_{i + 1}}$$

4. 状态机模型

大盗阿福

(1) 闫氏DP分析法
$$DP \begin{cases} 状态表示f[i] \begin{cases} 集合：从前i家偷的所有合法方案 \\\\ 属性：最大收益 \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 偷第i家店铺 \to f[i - 2] + w[i] \\\\ 不偷第i家店铺 \to f[i - 1] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

(2) 状态机

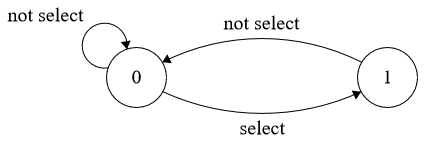
• 0: 未选最后一个店铺
• 1: 选最后一个店铺

$$DP \begin{cases} 状态表示f[i, 0], f[i, 1] \begin{cases} 集合：所有走了i步，且当前位于状态j（0/1）的所有走法 \\\\ 属性：最大收益 \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} f[i, 0] \begin{cases} 最后一步从0到0 \to f[i - 1, 0] \\\\ 最后一步从1到0 \to f[i - 1, 1] \\\\ \end{cases} \\\\ f[i, 1]：只有一种走法，最后一步从0到1 \to f[i - 1, 0] + w[i] \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

股票买卖IV

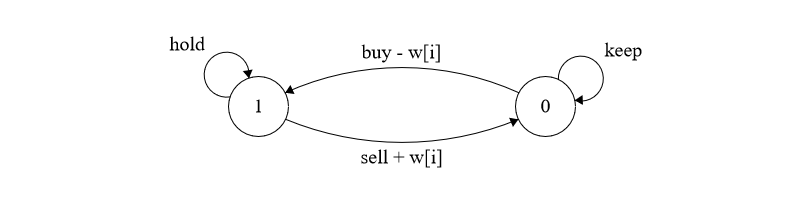
• 0：手中无货
• 1：手中有货

$$DP \begin{cases} 状态表示 \\\\ f[i, j, 0/1] \begin{cases} 集合： \begin{cases} f[i, j, 0]：所有经过了i天，已经进行过j场交易，\\\\ 且手中无货的所有集合 \\\\ f[i, j, 1]：所有经过了i天，已经进行过j - 1场交易，\\\\ 且手中有货正在进行第j场交易的所有集合 \\\\ \end{cases} \\\\ 属性：最大收益 \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} f[i, j, 0] = max(f[i - 1, j, 0], f[i - 1, j, 1] + w[i]) \\\\ f[i, j, 1] = max(f[i - 1, j, 1], f[i - 1, j - 1, 0] - w[i]) \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

股票买卖V

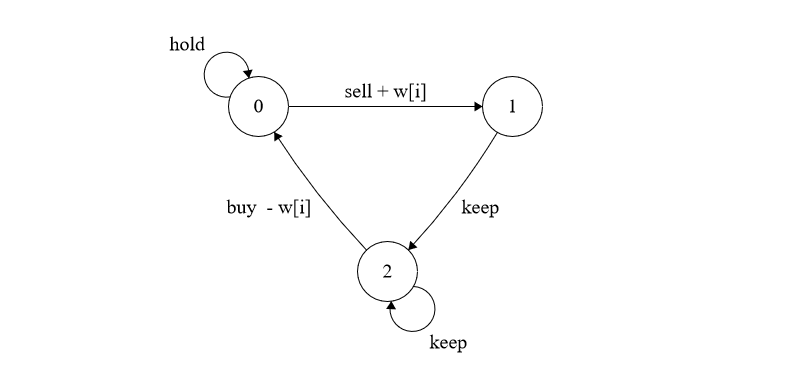
• 0：手中有货
• 1：手中无货的第一天
• 2：手中无货多于一天

$$\begin{cases} f[i, 0] = max(f[i - 1, 0], f[i - 1, 2] - w[i]) \\\\ f[i, 1] = f[i - 1, 0] + w[i] \\\\ f[i, 2] = max(f[i - 1, 1], f[i - 1, 2]) \end{cases} \\\\ $$

设计密码

$f[i, j]$表示当密码（长度为$n$）已经设计到第$i$位时，匹配串（长度为$m$）已经匹配到第$j$位的所有方案，由于最后设计的密码不能包含匹配串，因此j不能跳到$m$，$j$跳的位置看成状态，每一次跳跃看成是状态转换，$j$往哪跳取决于密码的第$i$位与匹配串的第$j+1$位的匹配情况。

5. 状压DP

• 棋盘式（基于连通性）DP
• 集合式DP

蒙德里安的梦想

1. 先放横着的，再放竖着的
2. 总方案数等于只放横着的小方块的合法方案数
3. 判断当前方案是否合法：所有剩余位置能否填满竖着的方块。可以按列来看，每一列内部所有连续的空着的小方块，需要是偶数个
4. 状态表示：f[i, j]表示已经将前i-1列摆好，且从第i-1列，伸出到第i列的状态是j的所有方案
5. 预处理出所有可能的状态转移避免超时

最短Hamilton路径

$$DP \begin{cases} 状态表示f[i, j] \begin{cases} 集合：所有从0走到j，走过的所有点是i的所有路径 \\\\ 属性：Min \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} 倒数第二个点是0 \to f[i - {j}, 0] + w[0, j] \\\\ 倒数第二个点是1 \to f[i - {j}, 1] + w[1, j]\\\\ \cdots 倒数第二个点是n-1 \to f[i - {j}, n-1] + w[n-1, j]\\\\ \end{cases} \\\\ \end{cases} \\\\ $$

骑士

$O(n * k * a * b), a * b \ll 2^n * 2^n$

1. $f[i, j, s]$表示所有只摆在前$i$行，已经摆了$j$个国王，并且第$i$行摆放状态是$s$的所有方案的集合
2. 对于某个状态，不能有两个1相邻
3. 相邻两行不能相互攻击到
4. 对于满足2、3性质的两行对应的状态，则存在状态转移：$f[i, j, a] += f[i - 1, j - count(a), b]$

$f[i, j, a]: 已经摆完了前i排，并且第i排的状态是a，第i-1排的状态是b，已经摆了j个国王的所有方案$
$f[i - 1, j - count(a), b]: 已经摆完了前i-1排，并且第i-1排的状态是b，已经摆了j-count(a)个国王\\\\ 的所有方案$

玉米田

$O(n * a * b), a * b \ll 2^m * 2^m$
$f[i, s]$表示所有只摆在前$i$行，且第$i$行摆放状态是$s$的所有方案的集合

炮兵阵地

$O(n * a * b * c), a * b * c \ll 2^m * 2^m * 2^m$
$f[i, j, k]$表示已经摆了前$i$行，且第$i$行摆放状态是$k$，第$i-1$行摆放状态是$j$的所有方案的集合

愤怒的小鸟

参考 题解

6. 区间DP

• 环形区间转链式区间
• 记录方案数
• 区间DP + 高精度
• 二位区间DP

石子合并

$O(n ^ 3)$

$f[i, j]$表示所有所有将第$i$堆到第$j$堆石子合并成一堆石子的合并方式

环形石子合并

$O(n ^ 3)$

1. 环形相对于链形的区别在于首尾的石子能合并
2. 很直接的一个想法就是枚举断开的位置，然后变成链形石子合并问题，就跟上题一样了；但这样做的时间开销是$O(n ^ 4)$，会超时
3. 类似旋转字符串那种思路，把环形链随机从一处断开然后复制一份接在后面，可以发现不同位置断开得到的$n$个链都包含在其中，这样最外一层的枚举就被消去了，时间开销还是$O(n ^ 3)$

棋盘分割

$f[x_1, y_1, x_2, y_2, k]$表示把子矩阵$(x_1, y_1)(x_2, y_2)$切分成$k$部分的所有方案

7. 树形DP

树的最长路径, 数字转换

找树的直径的步骤：
1. 任取一点作为起点，找到距离该点最远的一个点$u$
2. 再找距离$u$最远的一个点$v$
3. 那么$u$和$v$之间的路径就是一条直径

所有路径的分类标准：按照路径中最高的点进行划分

树的中心

点$i$到树中其他节点的距离可以分为两类
1. 以该点为根往下走的点
2. 以该点为根往上走的点

第一类距离的求法跟树的直径一样
第二类距离的求法又分两种情况（假设$i$的父节点是$u$）
1. 父节点$u$往下走的最长路径穿过了点$i$
2. 父节点$u$往下走的最长路径没有穿过点$i$

二叉苹果树

$f[i, j]表示以i为根的子树中选j条边的最大价值$

战略游戏

1. 每条边都要被观察到
2. $f[i, 0]$：父节点$i$没有放，所以所有子节点$j$一定要放，这样中间的边才能被观察到
3. $f[i, 1]$：父节点$i$放了，那么子节点$j$可放可不放，选择放置数量较小的方案即可

$$DP \begin{cases} 状态表示 \begin{cases} 集合： \begin{cases} f[i, 0]：以i为根节点，且i处不放士兵的所有摆放方案 \\\\ f[i, 1]：以i为根节点，且i处放置士兵的所有摆放方案 \\\\ \end{cases} \\\\ 属性：最小数量 \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} f[i, 0] = \sum f[j, 1] \\\\ f[i, 1] = \sum min(f[j, 0], f[j, 1]) \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

皇宫看守

1. 每个点都要被观察到
2. $f[i, 0]$：父节点$i$没有放警卫，所以子节点$j$只有两种情况
3. $f[i, 1]$：父节点$i$需要被子节点$j$看到，至少需要一个子节点能看到父节点即可
4. $f[i, 2]$：子节点$j$有三种情况

$$DP \begin{cases} 状态表示 \begin{cases} 集合： \begin{cases} f[i, 0]：以i为根节点，且i被父节点看到的所有摆放方案 \\\\ f[i, 1]：以i为根节点，且i被子节点看到的所有摆放方案 \\\\ f[i, 2]：以i为根节点，且在i上放置警卫的所有摆放方案 \\\\ \end{cases} \\\\ 属性：最小花费 \\\\ \end{cases} \\\\ \\\\ 状态计算 \begin{cases} f[i, 0] = \sum min(f[j, 1], f[j, 2]) \\\\ f[i, 2] = \sum min(f[j, 0], f[j, 1], f[j, 2]) \\\\ f[i, 1] = Min_{k}\(f[k, 2] + \sum_{j \neq k} min(f[j, 1], f[j, 2])\) \\\\ \end{cases} \\\\ \end{cases} \\\\ $$

8. 数位DP

1. 绝大多数的数位DP问题题面都是求区间$[L, R]$中满足某种性质的数的个数（或其他的值，比如求和等等）
2. 常用的策略就是将其转化为$[0, L - 1]$、$[0, R]$两个区间求解
3. 预处理DP + 分类讨论解决问题

$对于一个n位数A = \overline{a_{n - 1}a_{n - 2} \cdots a_2a_1}，可按如下方式划分成不同的集合$

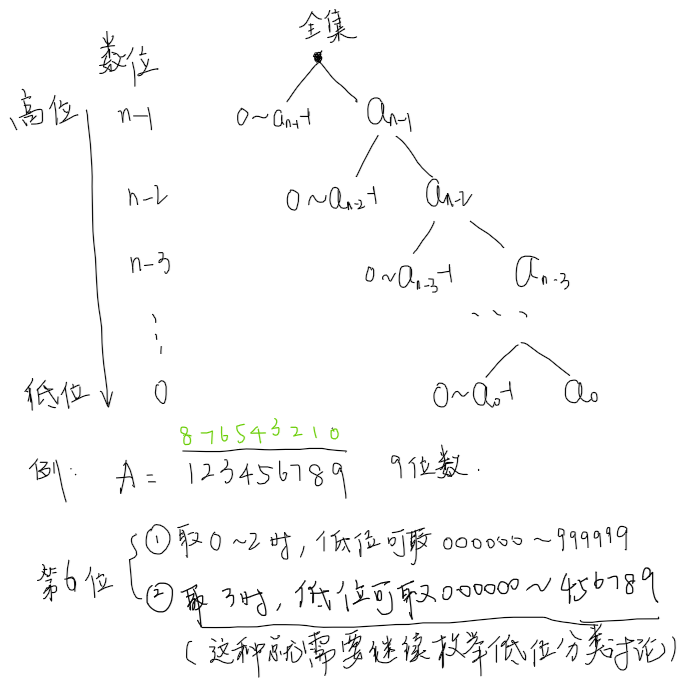
度的数量

1. 性质：恰好等于$K$个互不相等的$B$的整数次幂之和的数
2. 等价于数表示成$B$进制，正好有$K$个1，其余位都是0
3. 从$n$位中选$k$位填1，其他位填0，需要用到组合数，因此先预处理出要用到的所有组合数
4. 枚举每一位分类讨论

$对于A的第i位x \begin{cases} 1. x = 0，只能取0，相当于该位不存在左分支，直接跳过 \\\\ 2. x = 1 \begin{cases} 可取0，低位随便选，C_{i}^{k - last}，last表示已经选了多少个1 \\\\ 可取1，需要继续枚举低位分类讨论 \end{cases} \\\\ 3. x > 1 \begin{cases} 可取0，低位随便选，C_{i}^{k - last} \\\\ 可取1，同样低位随便选，C_{i}^{k - last - 1} \\\\ 不能取大于1的数，不满足性质了，结束枚举 \end{cases} \\\\ \end{cases} \\\\ 最后如果能枚举到第0位，且合法，那么A本身也是满足性质的数$

数字游戏

1. 性质：从高位到低位每一位的数字呈非降序排列
2. 需要预处理出满足性质的不降数，按位数划分集合
3. 在数位DP中常见的状态定义：$f[i, j]$表示一共有$i$位且最高位是$j$的满足某种性质的数的集合，这里的性质就是“不降数”

$DP \begin{cases} 状态表示 f[i, j] \begin{cases} 集合：所有最高位是j，且一共有i位的不降数的集合\\\\ 属性：Count \\\\ \end{cases} \\\\ \\\\ 状态计算：第i位填了j，则第i-1位只能填j \sim 9中的数，假设填的数是k，\\\\ 则 f[i, j] = \sum_{k \in [j, 9]}f[i - 1, k] \end{cases} \\\\ $

Windy数

1. 状态表示：$f[i, j]表示最高位是j的i位数的所有Windy数的集合$
2. 状态计算：$f[i, j] = \sum_{k \in [0, 9]}f[i - 1, k], |j - k| \geq 2$

数字游戏II

1. 状态表示：$f[i, j, k]表示最高位是j的i位数，且所有数位的和模N的余数是k的所有数的集合$
2. 状态计算：$f[i, j, k] = \sum_{x \in [0, 9]}f[i - 1, x, mod(k - j, N)]$

不要62

1. 性质：数字中不能出现子串4和62
2. 状态表示和状态计算注意细节

恨7不成妻

1. 性质：数字中不含7；各位数字之和模7不为0；不是7的整数倍
2. 状态表示：$f[i, j, a, b]表示最高位是j的i位数，且数本身模7的余数是a，各位数之和模7的余数是b的所有数的平方和$
3. 状态计算：
4. 本题的数据范围很大，若不频繁求模削弱数据范围，很容易造成数据溢出
   • 预处理10的幂时，记得求模
   • 每当可能乘一个很大的数时，先对它求模
   • 乘法运算得到的结果也可能很大，需要对它求模
   • 最后依据前缀和的思想求得的结果可能为负值，也需要求模

9. 单调队列优化DP

最大子序和

1. 求区间和，会直接想到前缀和
2. 暴力做法：枚举区间的右端点，对于每个右端点，向左枚举最长为$m$的区间左端点，更新答案
3. 暴力法时间开销$O(n ^ 2)$
4. 可以发现每次枚举都是固定右端点，再遍历左端点，左端点是会被重复枚举的
5. 因此考虑使用单调队列维护最大长度为$m$的从左至右单调递增的下标队列，只有左端点对应前缀和尽量小，区间和才会尽量大

修剪草坪

$$DP \begin{cases} 状态表示f[i] \begin{cases} 集合：从前i头牛中选，且合法的所有方案 \\\\ 属性：最大效率 \\\\ \end{cases} \\\\ \\\\ 状态计算： \begin{cases} 不选第i头牛 f[i - 1] \\\\ 选第i头牛，枚举最后一组连续选的牛的区间长度 f[i - j - 1] + s[i] - s[j] \\\\ \end{cases} \\\\ 状态转移方程：f[i] = max{f[i - 1], max{f[i - j - 1] + s[i] - s[j]]}}, 1 \leq j \leq k \end{cases} \\\\ $$

旅行问题

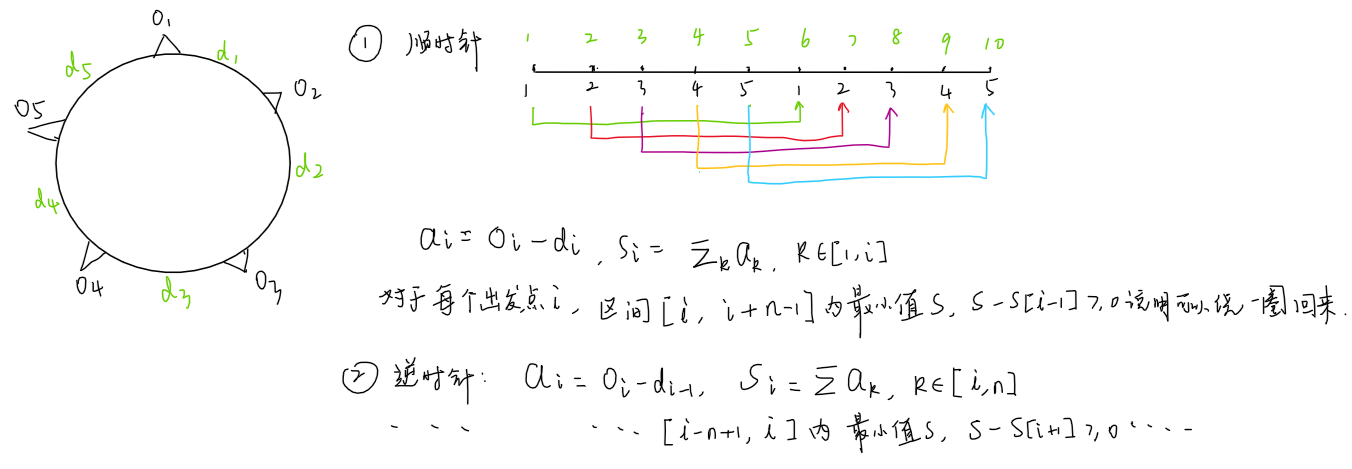
烽火传递

$$DP \begin{cases} 状态表示f[i] \begin{cases} 集合：前i座烽火台中第i座点火的所有点火方式的集合 \\\\ 属性：最小花费 \\\\ \end{cases} \\\\ \\\\ 状态计算：f[i] = min{f[j]} + w[i], j \in [i - m, i - 1] （维护一个长度为m的区间的最小值） \end{cases} \\\\ $$

绿色通道

二分+烽火传递

10. 斜率优化的DP

任务安排

运输小猫