欧拉函数

原题链接：873. 欧拉函数 - AcWing题库

解题思路

欧拉函数：ϕ(n) = n * (1 - 1/p1) + n * (1 - 1/p2)…

欧拉函数的证明：

p1、p2……为n的质因子

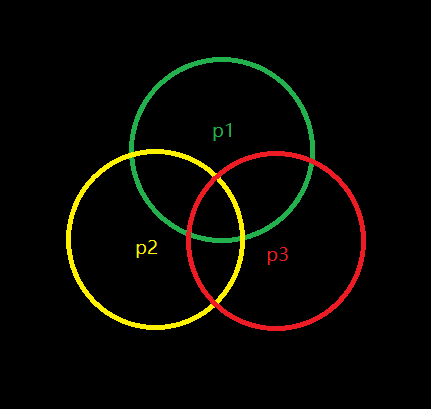
p1,p2,p3为n的质因子

我们可以用容斥原理证明——我们先减去那n以内的n的质因子倍数（n/p1、n/p2和n/p3）(三个圈)

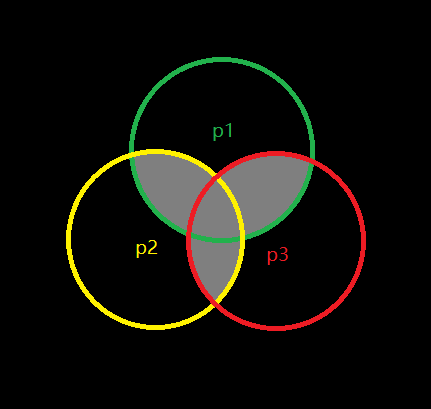
但是我们发现会有一些数被多加了——两个质因子的公倍数（n/p1p2、n/p2p3和n/p1p3）（灰色部分）

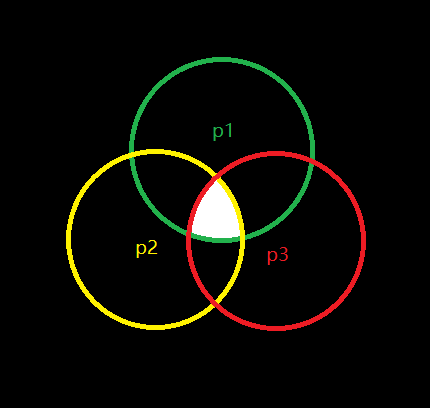
最后我们发现有一些部分被多加了——三个质因子的公倍数（n/p1p2p3）（白色部分）

ϕ(n) = n - n/p1 - n/p2 - n/p3 + n/p1p2 + n/p2p3 + n/p1p3 - n/p1p2p3

ϕ(n) = n * (-1/p1 - 1/p2 - 1/p3 + 1/p1p2 + 1/p2p3 + 1/p1p3 - 1/p1p2p3)

ϕ(n) = n * (1 - 1/p1) + n * (1 - 1/p2) + n * (1 - 1/p3)

化简后ϕ(n) = n * ((p1 - 1)/p1) * ((p2 - 1)/p2) * ((p2 - 1)/p2)

知道欧拉函数之后我们用一个分解质因数的程序加上欧拉函数就可以做出这道题

源代码

#include <iostream>
#include <cstdio>

using namespace std;

int main()
{
    int n;
    scanf("%d",&n);
    for(int x = 0;x < n;x ++)
    {
        int a;
        scanf("%d",&a);
        int b = a;
        int re = a;
        for(int i = 2;i <= a / i;i ++)
        {
            if(b % i == 0)
            {
                int s = 0;
                while(b % i == 0)
                {
                    s ++;
                    b /= i;
                }
                re = re / i * (i - 1);//欧拉函数，这样写可以防止小数
            }
        }
        if(b > 1)//大于sqrt(a)的质因子
        {
            re = re / b * (b - 1);
        }
        printf("%d\n",re);
    }
    return 0;
}