LCP 11. 期望个数统计

AC by : 胡图图

算法:贪心 O(n)

因为不同的数相互独立，考虑一段相同的数，假设长度为k,那么每个位置一一对应的概率为1/k，期望就是k * (1 / k),所以答案就是不同的数的数量。

class Solution {
public:
    int expectNumber(vector<int>& scores) {
        set<int> s;
        for(auto x : scores)
            s.insert(x);
        int res = s.size();

        return res;
    }
};

LCP 12. 小张刷题计划

AC by : 七月听雪眠

算法 : 二分 O(n * log(n))

二分答案然后check，check就是用最佳策略（最大的跳过）然后看书，看能不能用m天看完所有书

class Solution {
public:
    int a[100010];
    int n;
    int h;
    bool check(int mid){
        int maxv=0;
        int cnt=1;
        int sum=0;
        for(int i=1;i<=n;i++){
            maxv=max(maxv,a[i]);
            if(sum+a[i]-maxv<=mid){
                sum+=a[i];
            }else{
                cnt++;
                sum=a[i];
                maxv=a[i];
            }
        }
        // cout<<cnt<<endl;
        return cnt<=h;
    }
    int minTime(vector<int>& time, int m) {
        int l=0,r=1e9;
        h=m;
        n=time.size();
        cout<<check(2)<<endl;
        for(int i=1;i<=n;i++)a[i]=time[i-1];
        while(l<r){
            int mid=l+r>>1;
            if(check(mid))r=mid;
            else l=mid+1;
        }
        return l;
    }
};

LCP 13. 寻宝

AC by : 滑稽_ωﾉ

ps : M = 开关数量

$算法 : 状压DP + bfs预处理 O(2 ^ M * M + M * N ^ 2)$

通过bfs预处理出每个开关以及石头堆到每个点之间的距离，然后状压DP

状压DP：对于f[i][j],对于开关开启状态为i,以及当前在哪个开关编号（石头编号），然后通过预处理好的距离，直接进行转移即可

 const int N = 110, M = N * N, INF = 0x3f3f3f3f;

struct PII{
    int x, y;
};

int n, m;
char s[N][N];
vector<PII> os, ms;
int d[N][N][N];
PII op, ed;

PII q[M];
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, -1, 0, 1};
void bfs(int u, int x, int y)
{
    d[u][x][y] = 0;
    int hh = 0, tt = -1;
    q[++ tt] = {x, y};

    while(hh <= tt)
    {
        PII t = q[hh ++];
        x = t.x, y = t.y;
        for(int i = 0; i < 4; i ++)
        {
            int a = x + dx[i], b = y + dy[i];
            if(a >= 0 and a < n and b >= 0 and b < m and s[a][b] != '#' and d[u][a][b] == INF)
            {
                d[u][a][b] = d[u][x][y] + 1;
                q[++ tt] = {a, b};
            }
        }
    }
}


const int P = 17, K = 1 << P;
int f[K][60];

class Solution {
public:

    int minimalSteps(vector<string>& maze) {
        memset(d, -1, sizeof d);
        memset(s, 0, sizeof s);
        memset(d, 0x3f, sizeof d);
        os.clear(),  ms.clear();

        n = maze.size(),  m = maze[0].size();

        for(int i = 0; i < maze.size(); i ++)
            for(int j = 0; j < maze[i].size(); j ++)
            {
                s[i][j] = maze[i][j];
                if(s[i][j] == 'O')  os.push_back({i, j});
                else if(s[i][j] == 'M')  ms.push_back({i, j});
                else if(s[i][j] == 'S')  op = {i, j};
                else if(s[i][j] == 'T')  ed = {i, j};
            }

        int p = ms.size();
        for(int i = 0; i < os.size(); i ++)  ms.push_back(os[i]);

        for(int i = 0; i < ms.size(); i ++)
            bfs(i, ms[i].x, ms[i].y);

        int q = ms.size();
        bfs(q, op.x, op.y);
        bfs(q + 1, ed.x, ed.y);

        if(!p)
        {
            int res = d[q][ed.x][ed.y];
            if(res == INF)  res = -1;
            return res;
        }

        memset(f, 0x3f, sizeof f);
        for(int i = p; i < q; i ++)
            f[0][i] = d[i][op.x][op.y];

        for(int i = 1; i < (1 << p); i ++)
        {
            for(int j = 0; j < p; j ++)              //  搬石头过去开机关
                if((i >> j & 1))
                    for(int k = p; k < q; k ++)
                        f[i][j] = min(f[i][j], f[i ^ (1 << j)][k] + d[k][ms[j].x][ms[j].y]);

            for(int j = p; j < q; j ++)
                for(int k = 0; k < p; k ++)
                    f[i][j] = min(f[i][j], f[i][k] + d[k][ms[j].x][ms[j].y]);

        }
        int res = INF;
        for(int i = 0; i < p; i ++)  res = min(res, f[(1 << p) - 1][i] + d[i][ed.x][ed.y]);
        if(res == INF)  res = -1;
        return res;
    }
};

LCP 14. 切分数组

AC by : 胡图图

ps: M 为数据范围

$算法 ： 线性DP + 优化 O(N * \sqrt{M})$

ps:可以用线性筛选优化成$O(N * \sqrt{M / ln(M)})$

f[i] 表示从1切到i为止的最小值。

根据题意：很容易得到一个结论，只要首尾公共素因子，即可转移，显然我们可以暴力去找，但是时间复杂度是$O(n ^ 2)$,这就启发我们记录每个素因子能转移到的最小值，然后我们可以直接分解i的a[i]的质因数去找到一个最小值，那么时间复杂度就降为$O(N * \sqrt{M})$了

const int N = 1e6 + 10;

int f[N],minv[N];

class Solution {
public:
    int n;
    int splitArray(vector<int>& nums) {
        memset(f,0,sizeof f);
        memset(minv,0x3f,sizeof minv);

        n = nums.size();

        for(int i=1;i<=n;i++)
        {
            int x = nums[i - 1];
            f[i] = f[i - 1] + 1;
            for(int j=2;j * j <= x;j ++ )
            {
                if(x % j == 0)
                {
                    f[i] = min(f[i],minv[j] + 1);
                    minv[j] = min(minv[j],f[i - 1]);
                    while(x % j == 0) x = x / j;
                }
            }

            if(x > 1) 
            {
                f[i] = min(f[i],minv[x] + 1);
                minv[x] = min(minv[x],f[i - 1]);
            }

        }
        return f[n];
    }
};

LCP 15. 游乐园的迷宫

AC by : (惨遭团灭)

很早七月听雪眠 就给出解法了，然后我2h多没写出来QWQ。。
我太菜了~

$ 算法:贪心O(n ^ 2 * log(n))$

贪心思路：起点选一个凸包上的点，然后对于字母’L’,则选斜率最小的，对于字母’R’,则选斜率最大的。（因为如果我们这样做，以’L’为例对于i，i-1和i的斜率最小，那么在选i+1的时候，我们无论选什么，都会满足条件。）

#define pii pair<int,int>

const int N = 1010;

pii p[N];
bool st[N];
int last;
int idx[N],top;

int mul(pii a,pii b)
{
    return a.first * b.second - b.first * a.second;
}

bool CMP(int a,int b)
{
    pii t1 = {p[a].first - p[last].first,p[a].second - p[last].second};
    pii t2 = {p[b].first - p[last].first,p[b].second - p[last].second};
    return mul(t1,t2) > 0;
}

class Solution {
public:
    int n;
    vector<int> visitOrder(vector<vector<int>>& points, string direction) {
        vector<int> res;
        n = points.size();

        for(int i=0;i<n;i++)
        {
            p[i] = {points[i][0],points[i][1]};
            st[i] = false;
        }

        int cur = 0;

        for(int i=1;i<n;i++)
            if(p[i].first < p[cur].first)
                cur = i;

        res.push_back(cur);
        last = cur;
        st[cur] = true;
        for(int i=0;i<n-2;i++)
        {
            last = cur;
            top = 0;
            for(int j=0;j<n;j++)
                if(!st[j])
                    idx[top ++ ] = j;

            sort(idx,idx + top,CMP);

            if(direction[i] == 'L')
                cur = idx[0];
            else
                cur = idx[top - 1];
            res.push_back(cur);
            st[cur] = true;
        }

        for(int i=0;i<n;i++)
            if(!st[i])
                res.push_back(i);

        return res;   
    }
};

LCP 16. 游乐园的游览计划
AC by : (惨遭团灭)

$ 算法:暴力 + 贪心 O (n ^ 2) $

通过固定一条边，然后找第三个点（两个点同时拥有的公共点），暴力找出所有的以该点为中心，所有满足条件的点对。

贪心思路：对于每个点为中心，除了下图情况最大点对和，一定会出现在最大值内，出现了下图情况我们就可以认为次大点对和一定会出现在最大值内。

ps : ABC为点对和
(B为最大值，但如果选B，则会阻断AC,致使答案可能会变小)

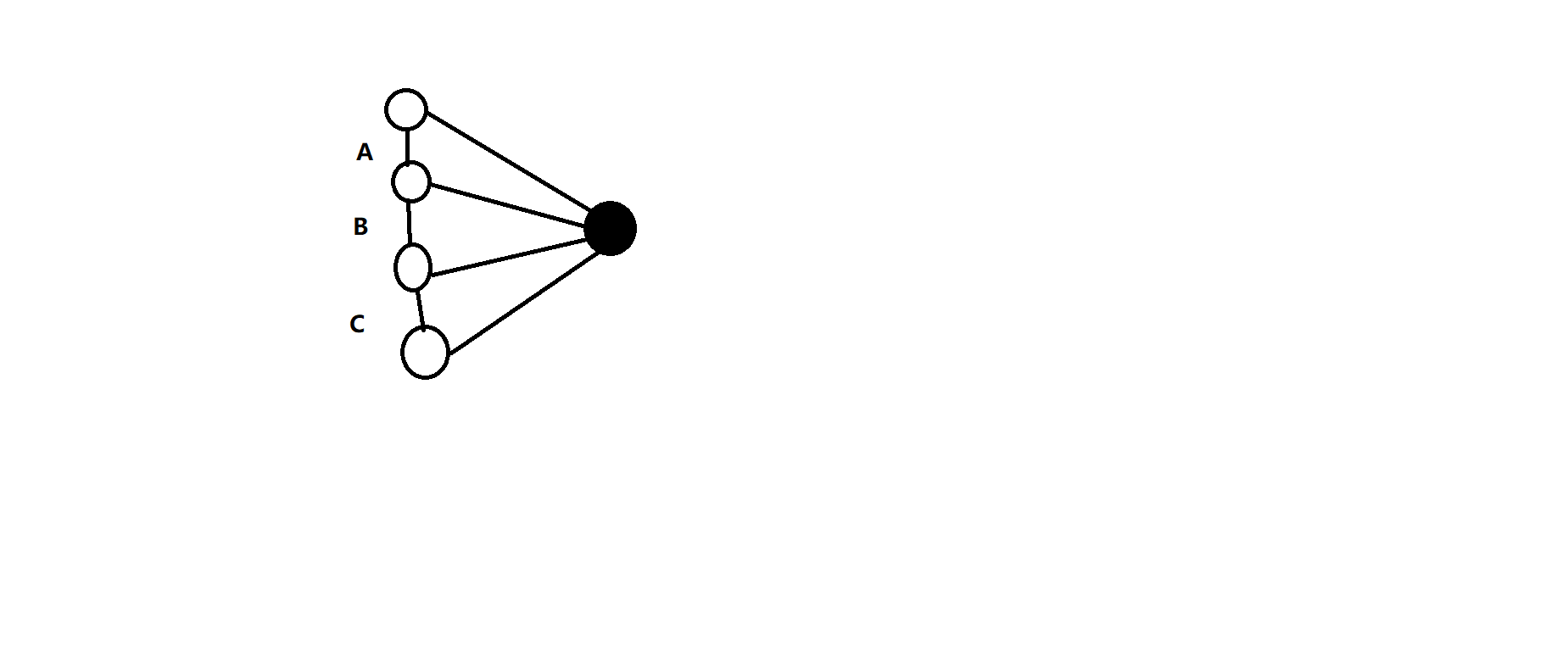
找到一个点对之后再暴力找另一个点对，这题就结束了。

#define pii pair<int,int>

const int N = 1e4 + 10;

int h[N],e[N << 1],ne[N << 1],idx;

int res;
int vis[N],stamp;
int n;

vector<pii> ver[N];
vector<int> w;

inline void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx ++ ;
}

inline bool CMP(pii &a,pii &b)
{
    return w[a.first] + w[a.second] > w[b.first] + w[b.second];
}

int calc(vector<pii> &a,pii &b)
{
    int res = -1;

    for(auto x : a)
    {
        int cur = w[x.first] + w[x.second];
        if(b.first != x.first && b.first != x.second) cur += w[b.first];
        if(b.second != x.first && b.second != x.second) cur += w[b.second];
        res = max(res,cur);
    }
    return res;
}

class Solution {
public:
    int maxWeight(vector<vector<int>>& edges, vector<int>& value) {

        w = value;
        n = value.size();

        for(int i=0;i<n;i++) ver[i].clear();

        res = stamp = idx = 0;

        memset(h,-1,sizeof h);
        memset(vis,-1,sizeof vis);

        for(auto x : edges)
        {
            add(x[0],x[1]);
            add(x[1],x[0]);
        }

        for(auto x : edges)
        {
            ++ stamp;
            int u = x[0],v = x[1];
            if(u > v) swap(u,v);
            for(int i=h[u];~i;i=ne[i])
            {
                int p = e[i];
                vis[p] = stamp;
            }
            for(int i=h[v];~i;i=ne[i])
            {
                int p = e[i];
                if(vis[p] == stamp)
                {
                    ver[p].push_back({u,v});
                }
            }

        }

        for(int i=0;i<n;i++)
        {
            sort(ver[i].begin(),ver[i].end(),CMP);
            auto it = ver[i].begin();
            for(int j=0;j<2 && it != ver[i].end();it++,j++)
            {
                int cur = calc(ver[i],*it);
                if(cur == -1) continue;
                res = max(res,w[i]+cur);
            }
        }

        return res;
    }
};