一维树状数组

引入：现在有一个包含n个数的数列2,7,3,41,4,99…,请你计算一下前i个数的和。
我们很容易想到暴力相加。

int sum = 0;
for (int k = 1; k <= i; k ++ )
    sum += a[k];

若是用这个办法，则复杂度就是O(n),而我要是修改a[i],则前缀和数组的sum[i],sum[i+1]…,sum[n]都要发生改变，修改前缀和数组最坏情况下又是O(n)。故我们使用树状数组来解决程序效率不高的问题。

功能

树状数组可以高效地计算数列的前缀和，其查询前缀和与点更新（修改）操作都可以在O(logn)时间内完成。

由来

树状数组引入了分级管理制度且设置了一个管理小组，管理小组中的每个成员都管理了一个或多个连续的元素。一般我们把管理小组数组开为c[].

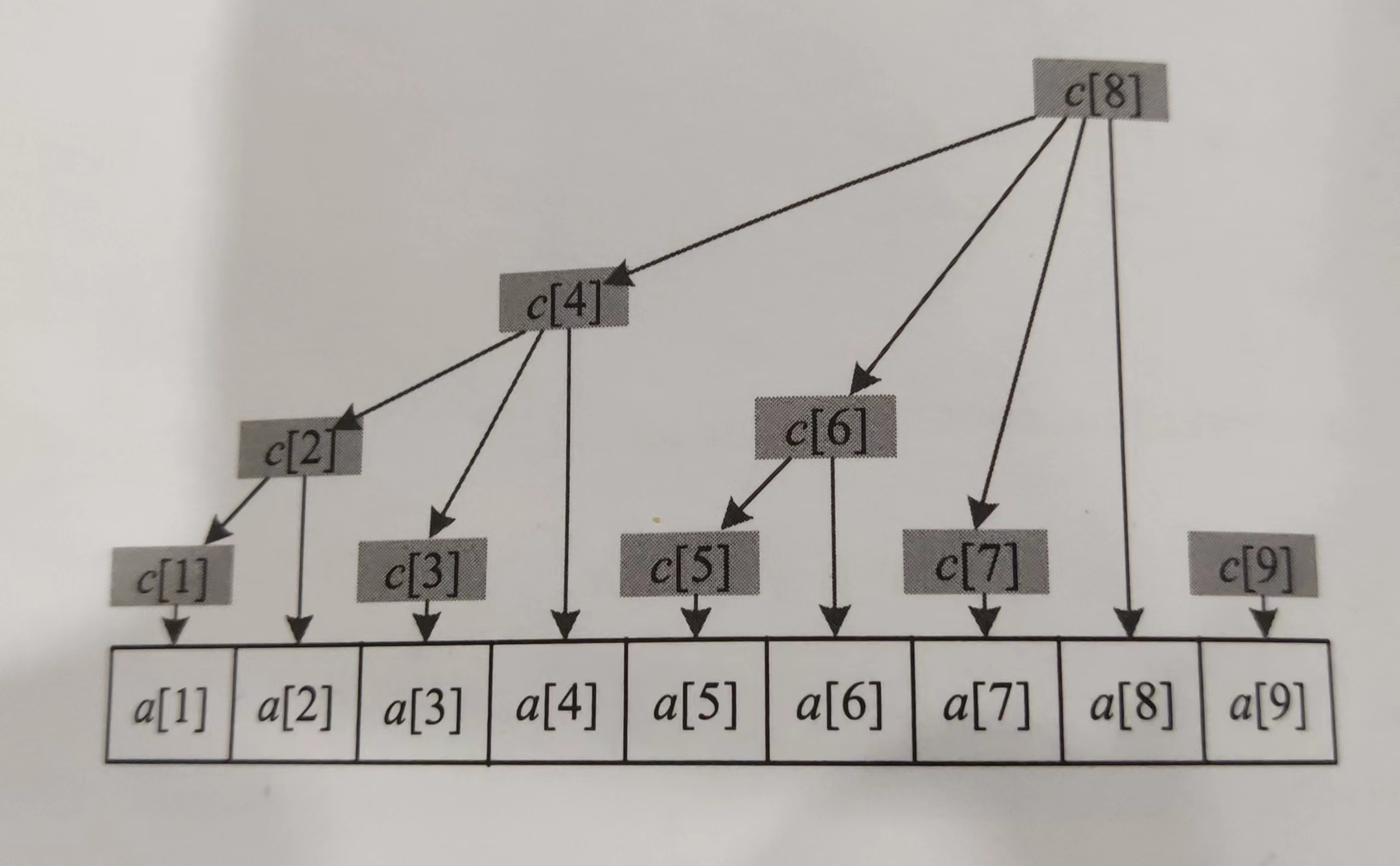
c[1]:存储a[1]
c[2]:存储c[1],a[2]的和，相当于存储a[1],a[2]的和
c[3]:存储a[3]
c[4]:存储c[2],c[3],a[4]的和，相当于存储a[1],a[2],a[3],a[4]的和
c[5]:存储a[5]
c[6]:存储c[5],a[6]的和，相当于存储a[5],a[6]的和
c[7]:存储a[7]
c[8]:存储c[4],c[6],c[7],a[8]的和，相当于存储a[1]~a[8]的和
c[9]:存储a[9]
我们可以看到这个管理数组c[]是树状的，所以我们命名为树状数组。

必备知识

树状数组，又叫作二进制索引树，通过二进制分解划分区间。
(1)lowbit操作
代码：

#define lowbit(x) -x&x

推导：
若i的二进制表示（即01串）的末尾有k个连续的0，则c[i]存储的区间长度为$2^k$.
即c[i]=a[i-$2^k$+1]+a[i-$2^k$+2]+…+a[i]

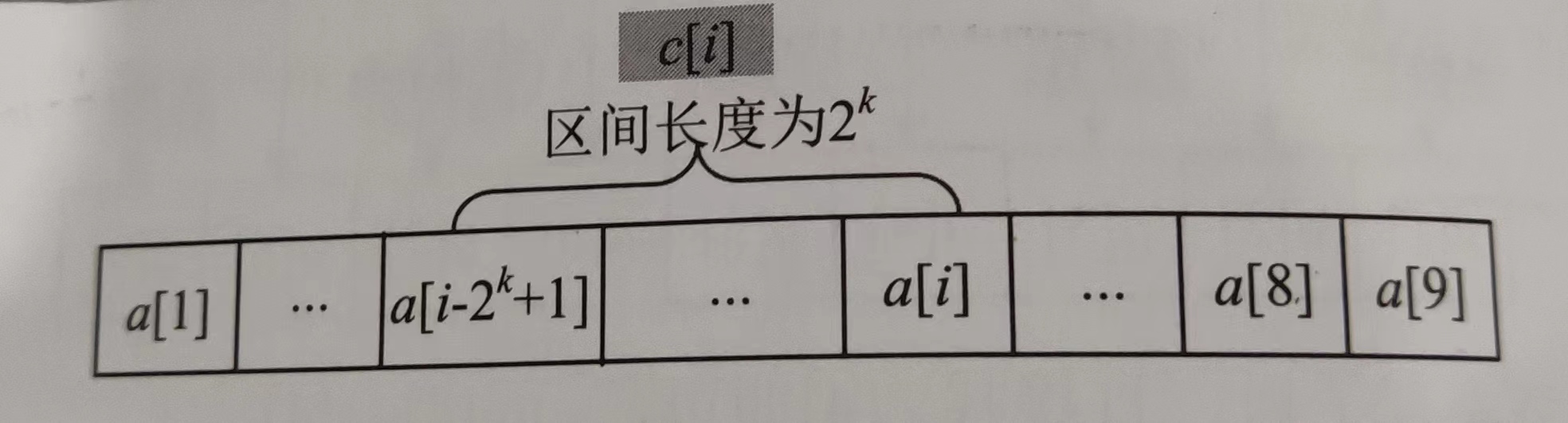
根据位运算和二进制的知识，我们不难得知c[i]的区间长度就是i的二进制表示下最低位的1以及它后面的0所构成的数值。
我们以10100（即20的二进制）为例，我们要得到100（十进制为4，$2^2$）.
首先我们可先对10100按位取反得01011,然后加1得01100.此时我们发现最低位的1和后面的0都和原表示一致，而前面的0与1都与原表示相反，此时我们只需再与原值10100进行与运算即可。
在计算机当中，二进制数采用补码表示，-i的补码就是i取反再加1，所以-i&i就是c[i]的区间长度
(2)前驱和后继
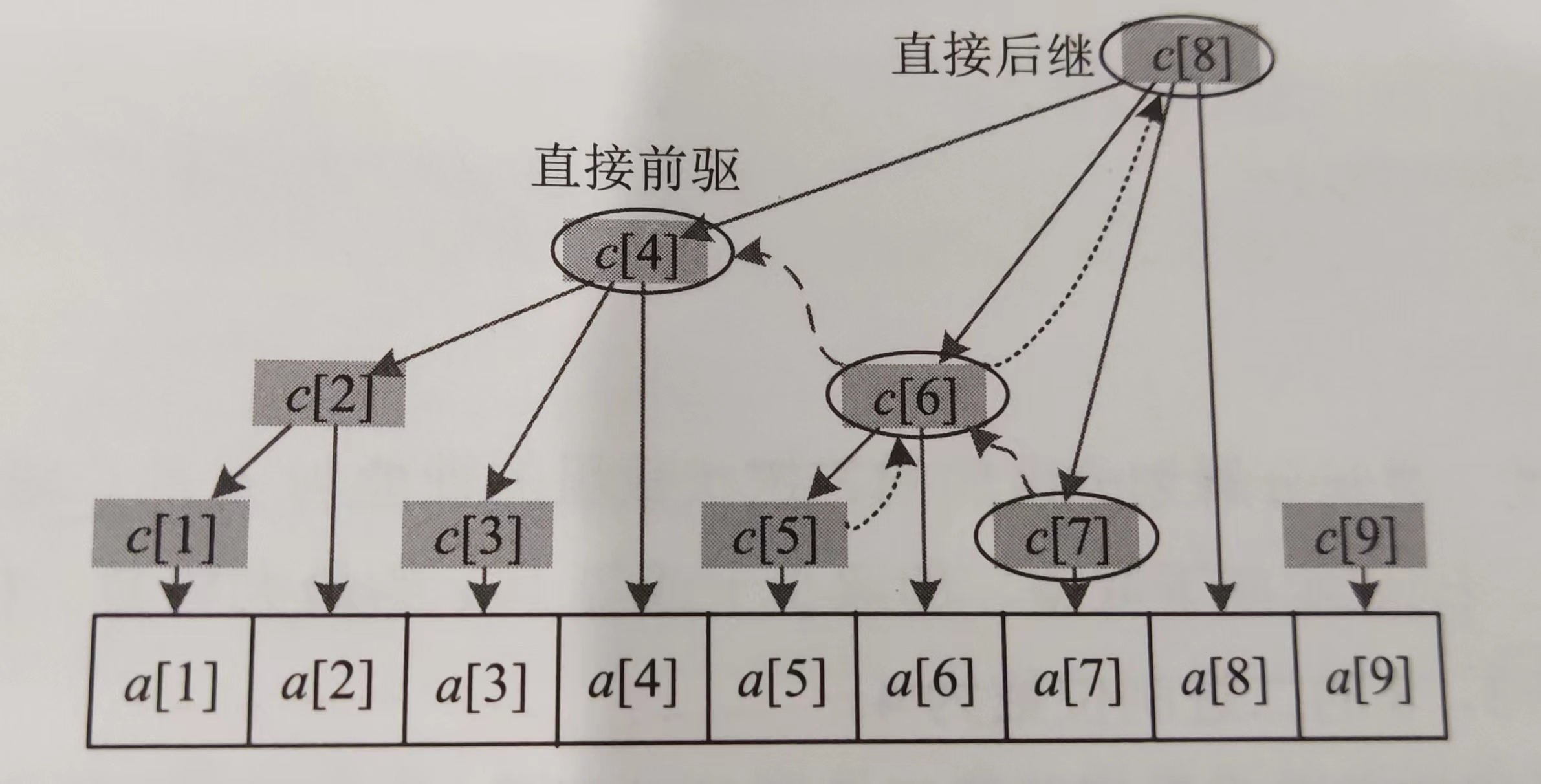
直接前驱：c[i]的直接前驱为c[i-lowbit(i)],即c[i]左侧紧邻的子树的根。
直接后继：c[i]的直接后继为c[i+lowbit(i)],即c[i]的父节点。
前驱：c[i]的直接前驱、其直接前驱的直接前驱等，即c[i]左侧所有子树的根。
后继：c[i]的直接后继，其直接后继的直接后继等，即c[i]的所有祖先。

查询前缀和

前i个元素的前缀和sum[i]等于c[i]+c[i]的前驱。

int sum(int i) {
    int s = 0;
    for (; i; i -= lowbit(i) )
        s += c[i];
    return s;
}
若查询[l,r]的和，sum(r)-sum(l-1);

点更新

若对a[i]进行修改，令a[i]加上一个数z，只需更新c[i]及其后继，令这些节点都加上z。

void add(int i, int z) {
    for (; i <= n; i += lowbit(i) )
        c[i] += z;
}

注：树状数值的下标从1开始，不能从0开始，因为lowbit(0)=0，会出现死循环。

分析时间复杂度

树状数组的性能与n的二进制位数有关，n的二进制位数为logn下取整+1
树高h=logn
查询前缀和与点更新的复杂度均为O(logn)

多维树状数组

m维树状数组的复杂度为$O(log^mn)$

查询前缀和

以二维为例

int sum(int x, int y) { // 求左上角(1,1)到右下角(x,y)的矩阵区间和
    int s = 0;
    for (int i = x; i; i -= lowbit(i) )
        for (int j = y; j; j -= lowbit(j) )
            s += c[i][j];
    return s;
}

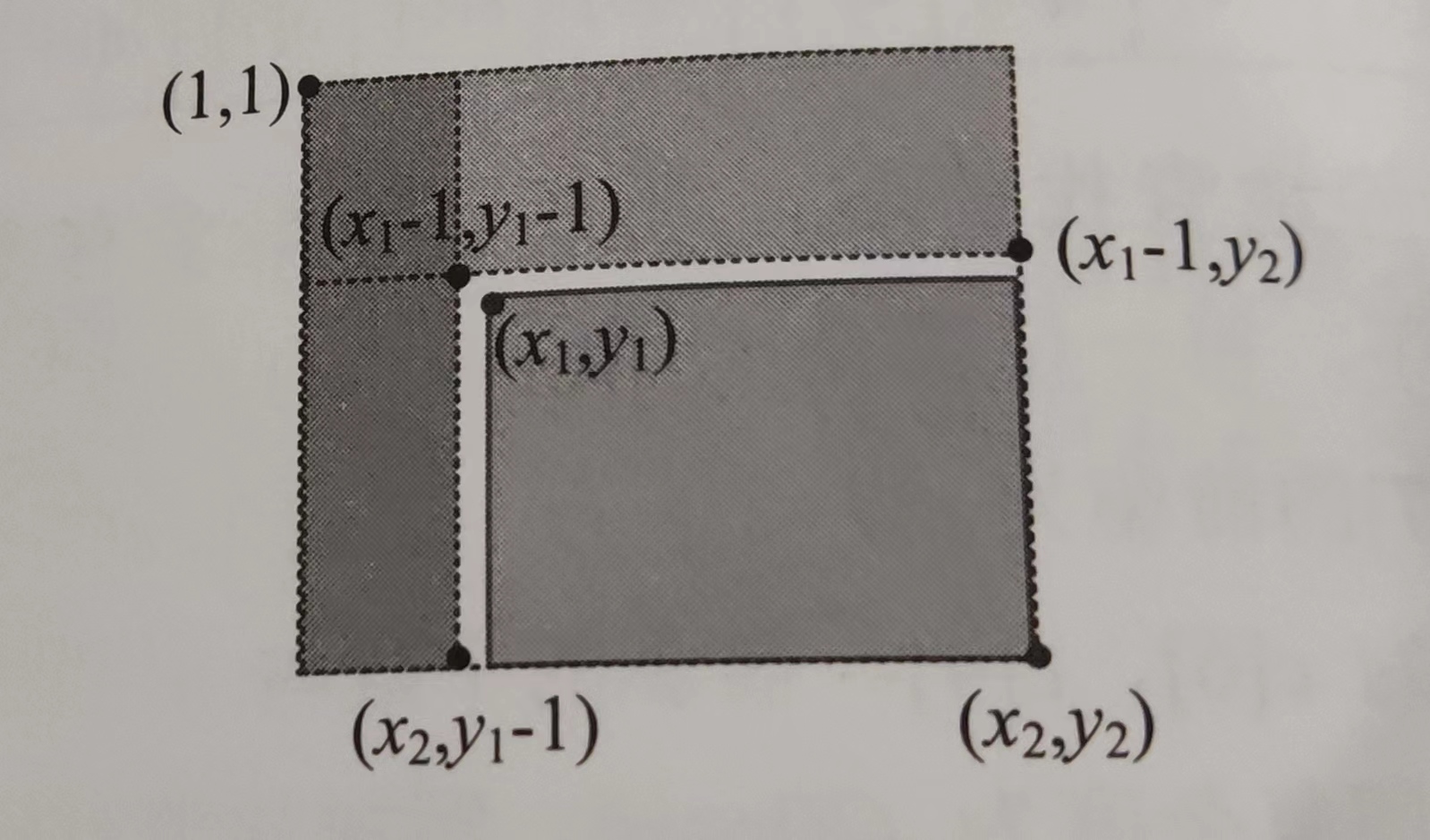
查询区间和可以参考**_二维前缀和的思想（容斥原理）_**
求左上角(x1, y1)到右下角(x2, y2)子矩阵的区间和?
sum(x2, y2) - sum(x1-1, y2) - sum(x2, y1-1) + sum(x1-1, y1-1)

点更新

以二维为例, 若对a[x][y]进行修改（+z）

void add(int x, int y, int z) {
    for (int i = x; i <= n; i += lowbit(i) )
        for (int j = y; j <= n; j += lowbit(j) )
            c[i][j] += z;
}

树状数组的局限性

树状数组主要用于查询前缀和、区间和以及点更新，对点查询、区间修改的执行效率较低。

减法规则：当问题满足减法规则时(例如求区间[l,r]的和，sum[l,r]=sum[r]-sum[l-1])，可以使用树状数组
不满足减法规则(例如求区间[l,r]的最大值)，此时可选择使用线段树解决。

扩展

引入差分数组b[], 用树状数组c[]维护b[]的前缀和(增量数组)
单点查询: 查询a[x]：a[x] + ask(x)
区间修改：给区间[l, r]中的每个数加上c：add(l, c), add(r + 1, -c)

引入差分数组b[]
引入树状数组c1(维护b[i]的前缀和(增量数组))和c2(维护b[i] * i的前缀和)
不方便(可以用更方便的线段树)
区间查询: 查询[l, r]的和：(s[r] + (r + 1) * ask1(r) - ask2(r)) - (s[l - 1] + l * ask1(l - 1) - ask2(l - 1))
区间修改：给区间[l, r]中的每个数加上c：add1(l, c), add1(r + 1, -c), add2(l, l * c), add2(r + 1, (r + 1) * -c)

树状数组能维护：和、异或和、min、max······

维护最值

void add(int x, int k) {
    for ( ; x <= n; x += lowbit(x)) {

        c[x] = k;

        for (int i = 1; i < lowbit(x); i <<= 1)

            c[x] = max(c[x], c[x - i]);
    }
}

int sum(int l, int r) {
    int res = 0;

    while (l <= r) {
        res = max(res, a[r]);
        r -- ;

        for ( ; l <= r - lowbit(r); r -= lowbit(r))

            res = max(res, c[r]);
    }

    return res;
}

例题

单点修改、区间查询

敌兵布阵

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 50010;

int t[N];
int c, n;
int casei;

int lowbit(int x) {
    return x & -x;
}

void add(int x, int k) {
    for ( ; x <= n; x += lowbit(x))

        t[x] += k;
}

int ask(int x) {
    int res = 0;

    for ( ; x; x -= lowbit(x))

        res += t[x];
    return res;
}

int main() {
    int T;
    scanf("%d", &T);

    while (T -- ) {
        memset(t, 0, sizeof t);
        scanf("%d", &n);

        for (int i = 1; i <= n; i ++ ) {

            scanf("%d", &c);
            add(i, c);
        }

        printf("Case %d:\n", ++ casei);
        char op[6];

        while (~scanf("%s", op)) {
            if (op[0] == 'E')
                break;
            int a, b;
            scanf("%d%d", &a, &b);

            if (op[0] == 'A')
                add(a, b);
            else if (op[0] == 'S')
                add(a, -b);
            else
                printf("%d\n", ask(b) - ask(a - 1));
        }
    }

    return 0;
}

区间修改、单点查询

Color the ball

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int t[N];
int n;

int lowbit(int x) {
    return x & -x;
}

void add(int x, int k) {
    for ( ; x <= N; x += lowbit(x))

        t[x] += k;
}

int ask(int x) {
    int res = 0;

    for ( ; x; x -= lowbit(x))

        res += t[x];
    return res;
}

int main() {
    while (~scanf("%d", &n)) {
        if (n == 0)
            break;
        memset(t, 0, sizeof t);

        for (int i = 1; i <= n; i ++ ) {

            int a, b;
            scanf("%d%d", &a, &b);
            add(a, 1), add(b + 1, -1);
        }

        for (int i = 1; i <= n; i ++ )

            if (i != n)
                printf("%d ", ask(i));
            else
                printf("%d\n", ask(i));
    }

    return 0;
}

求逆序对

Minimum Inversion Number

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 5010, INF = 0x3f3f3f3f;

typedef long long LL;

int tree[N], arr[N];
int n;

int lowbit(int x) {
    return x & -x;
}

void add(int x) {
    for ( ; x <= n; x += lowbit(x))

        tree[x] ++ ;
}

int ask(int x) {
    int res = 0;

    for ( ; x; x -= lowbit(x))

        res += tree[x];
    return res;
}

int main() {
    while (~scanf("%d", &n)) {
        memset(tree, 0, sizeof tree);

        for (int i = 1; i <= n; i ++ )

            scanf("%d", &arr[i]);

        LL ans = INF;
        LL cnt = 0;

        for (int i = 1; i <= n; i ++ ) {

            add(arr[i] + 1);
            cnt += i - ask(arr[i] + 1);
        }

        ans = cnt;

        for (int i = 1; i <= n; i ++ ) {

            cnt = cnt - arr[i] + n - 1 - arr[i];
            ans = min(ans, cnt);
        }

        printf("%lld\n", ans);
    }

    return 0;
}