前言

传送门 :
难得用大号打一次,差点掉分
因为太菜都没有时间看E

A.

题意 :
给定一个$a[]$,询问是否可以通过操作使得其变为升序排序

操作如下 :
对于$i,j\ a[i]*a[j]<0$则$a[i]=-a[i],a[j]=-a[j]$

思路 :
因为不存在交换(听说很多人读错)

因此我们只需要按序枚举,对于当前的$i$

如果$a[i]<0$的话,显然可以提供一次操作的机会,因此我们令$a[i]=-a[i],++cnt$

因为数组必须是升序,也就是所有负号都应该在左边,所以我们根据可以操作的次数进行修改,然后判断即可

code :

void solve(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];

    int cnt = 0;
    for(int i = 1;i<=n;i++){
        if(a[i] < 0){
            cnt++;
            a[i] = -a[i];
        }
    }

    for(int i=1;i<=cnt;i++){
        a[i] = -a[i];
    }
    for(int i=2;i<=n;i++){
        if(a[i] < a[i-1]){
            cout<<"NO"<<endl;
            return;

        }
    }
    cout<<"YES"<<endl;
}

B.

题意 :
给定一个$s$和一个字符数组$ch[]$,询问最多可以进行多少次操作

操作定义如下 :
对于每次操作,寻找所有的$s[i]=ch[i]$删除$s[i-1]$

思路 :
因为数据范围很大,考虑$O(n)$

显然对于$s[i]\in ch[]$我们都需要考虑计算答案

对于每次计算答案之后,因为每次操作

都是对整个数组进行操作, 所以我们的$ans$ 不能往后继续累加,所以$ans=1$

因此,如此反复计算即可

处理和思维方式有点类似于贡献

code :

void solve(){
    cin>>n;
    string s;cin>>s;
    int m;cin>>m;

    for(int i = 'a' ;i<='z' ; i ++ )st[i] = 0 ;
    for(int i = 0 ;i <m;i++){
        getchar();char c;cin>>c;
        st[c] = 1;
    }

    int cnt = 0;
    int maxn = 0 ;

    for(int i = 0; i<n;i++){
        if(st[s[i]]){
            maxn = max(maxn,cnt);
            cnt = 1;
            continue;
        }else cnt++;
    }
    cout<<maxn<<endl;
}

signed main(){
    int t;cin>>t;while(t--)
    solve();
    return 0 ;
}

C.

思路 :
给定$a[]$,$b[]$,$d[]$,询问$c[]$有多少种合法方案

合法 : 指的是$c[]$是$1-n$的排列
数组的关系 : 对于$c[i]=d[i](d[i]\neq0)$,$c[i]=a[i]orb[i](d[i]==0)$

思路 :

对于样例$1$进行分析
$1\ 2\ 3\ 4\ 5\ 6\ 7$
$2\ 3\ 1\ 7\ 6\ 5\ 4$
$2\ 0\ 1\ 0\ 0\ 0\ 0$

为了使得最后是$1-n$的排列我们就需要保证不出现重复

观察样例我们会发现$a[]={1,2,3}和b[]={2,3,1}$构成了一个环,但是因为$b[]$的两个数已经确定你,所以对于$c[2]$就固定了

但是对于$a[]={5,6},b[]={6,5}$和$a[]={4,7},b={7,4}$这两个每个环都有$2$种选择

因此根据乘法原理$2^2$所以我们只需要找环即可

code :

const int N = 5e5+10,mod  = 1e9+7;

int in[N],flag[N];
int nxt[N];
int a[N],b[N],c[N];

int n;
// int st[N];

ll qmi(ll a,ll b){
    ll res = 1;
    while(b){
        if(b&1) res = res*a%mod;
        a = a*a%mod;
        b >>=1;
    }
    return res;

}
void solve(){
    cin>>n;

    for(int i=1;i<=n;i++)in[i]=0,flag[i]=0;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>nxt[a[i]];

    for(int i=1;i<=n;i++){
        int x;cin>>x;
        in[x] = 1;

    }
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        int ok=1;
        if(flag[i])continue;
        int cur=i,sz=0;
        while(!flag[cur])
        {
            sz++;
            flag[cur]=1;
            if(in[cur])ok=0;
            cur=nxt[cur];
        }
        if(sz==1)ok=0;
        cnt+=ok;
    }
    cout<<qmi(2,cnt)<<endl;
}

D.

题意 :
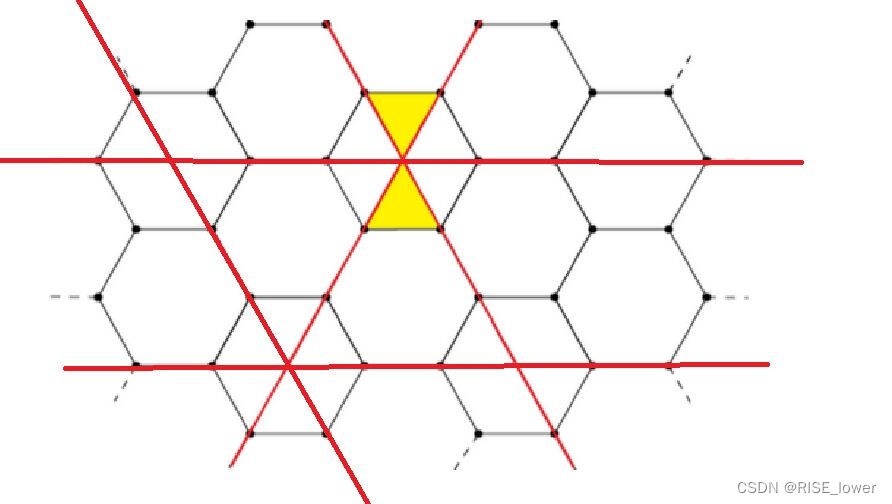
给定一个蜂窝,问需要切多少刀,才有$n$个等边三角形

思路 :
(这里就是数学基础或者天赋题了,我感觉)

首先肯定是去$OEIS$找,结果没找到

那么只能手画了,通过手画出来的规律我们会发现
$0,1,2 |2,3,4|4,5,6$
当然因为对称应该是$0,2,4|4,6,8|8,10,12$
然后对其求一个前缀和在进行二分即可

(图片来源于群友)

code :

const int N = 1e5+10 ;
const ll MAXN = 1e9;

ll b[N];
ll sum[N];

int idx =3;

void init(){
    b[1] = 0;
    sum[1]  = 0 ;
    b[2] = 2;
    sum[2] =2;
    b[3] = 4;
    sum[3] = 6;



    for(int i=4;i<=N;i++){
        b[i] = ((b[i-3]/2)+2)*2;
        sum[i] = sum[i-1]+b[i];
        ++idx;
        if(sum[i] > MAXN) return;
    }

}
void solve(){

    ll n;cin>>n;

    ll l = 1,r = idx;
    while(l<=r){
        ll mid = (l+r)/2;
        if(sum[mid] >= n)r =mid-1;
        else l = mid+1;
    }
    cout<<l<<endl;


}

int main(){
    init();
    for(int i=1;i<=idx;i++)cout<<sum[i]<<" ";
    cout<<endl;

    int t;cin>>t;while(t--)
    solve();
    return 0 ;
}