背包问题

01背包

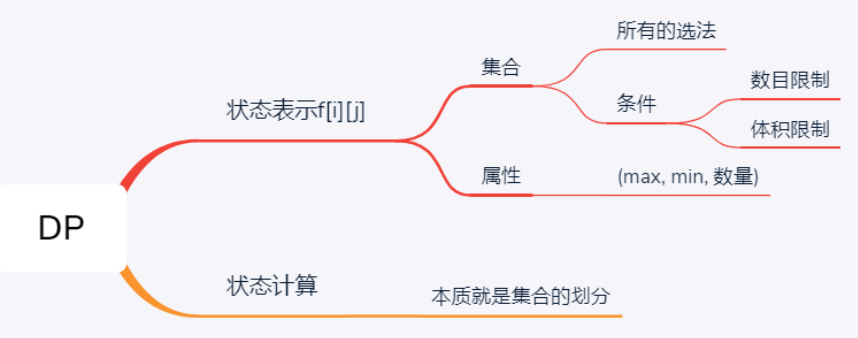
状态f[i][j]定义：前 $i$ 个物品，背包容量 $j$ 下的最优解（最大价值）

二维：状态转移方程dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i])

f[i-1][j]:不选第 $i$ 个物品的集合中的最大值
f[i-1][j-v[i]]+w[i]:选第 $i$ 个物品的集合,但是直接求不容易求所在集合的属性,先将第 $i$ 个物品的体积减去,求剩下集合中选法的最大值

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++)
        {
            f[i][j] = f[i - 1][j];//如果不选，那么f[i][j]就等于上一个不包含i的f[i - 1][j]
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);//包含i，就要选一下
        }

    cout << f[n][m] << endl;

    return 0;
}

一维优化版

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= v[i]; j --)
            if(j >= v[i]) f[j] = max(f[j], f[j - v[i]] + w[i]);
//f[i] 仅用到了f[i-1]层, j与j-v[i] 均小于j,若用到上一层的状态时,从大到小枚举, 反之从小到大哦

    cout << f[m] << endl;

    return 0;
}

完全背包问题

朴素版

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++ ) cin >> v[i] >>w[i];

    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= m; j ++)
            for(int k = 0; k * v[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + w[i] * k);

    cout << f[n][m] << endl;
}

二维优化版

dp[i][j - v] = max(dp[i - 1][j - v], dp[i - 1][j - 2 * v] + w, dp[i - 1][j - 3 * v] + 2 * w, .....)；
而我们需要的dp[i][j]的状态表示是：
dp[i][j]= max(dp[i - 1][j], dp[i - 1][j - v] + w, dp[i - 1][j - 2 * v] + 2 * w, dp[i - 1][j - 3 * v] + 3 * w);
将每一项一一比对，我们可以得到下列状态表示:
dp[i][j] = max(dp[i - 1][j], dp[i][j - v] +w)；

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= m; j ++)
        {
            f[i][j] = f[i - 1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;

    return 0;
}

一维优化版

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i ++)
        for(int j = 0; j <= m; j ++)
        {
            if(j >= v[i]) f[j] = max(f[j], f[j - v[i]] + w[i]);
        }

    cout << f[m] << endl;

    return 0;
}

多重背包问题一

朴素版

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];

    for(int i = 1; i<= n; i ++)
        for(int j = 0; j <= m; j ++) 
            for(int k = 0; k <= s[i] && k * v[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);

    cout << f[n][m] << endl;

    return 0;
}

多重背包问题二

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 25000, M = 2010;

int n, m;

int v[N], w[N];
int f[M];

int main()
{
    cin >> n >> m;

    int cnt = 0;//分的组
    for(int i = 1; i <= n; i ++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;//组里的个数
        while(k <= s)
        {
            cnt ++;//组数 + 1
            v[cnt] = a * k;//整体体积
            w[cnt] = b * k;//整体价值
            s -= k;
            k *= 2;
        }

        if(s > 0)//剩下的
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }

    }

    n = cnt;

    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;


    return 0;
}

分组背包问题

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;

    for(int i = 1; i <= n; i ++)
    {
        cin >> s[i];
        for(int j = 0; j < s[i]; j ++)
            cin >> v[i][j] >> w[i][j];
    }

    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= 0; j --)
            for(int k = 0; k < s[i]; k ++)
                if(v[i][k]<= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;

    return 0;
}