李超线段树

首先，引入一道例题：
[HEOI2013]Segment
题目大意：

维护两种操作。
1. 插入一条 $(x_0,y_0)$ 到 $(x_1,y_1)$ 的线段。
2. 查询与直线 $x=k$ 相交的线段中，交点 $y$ 坐标最大的那条线段的编号（若有多个，则输出编号最小的那个）。

Ex

1. 插入 $((11,4),(5,14))$ 和 $((19,19),(8,10))$。
   
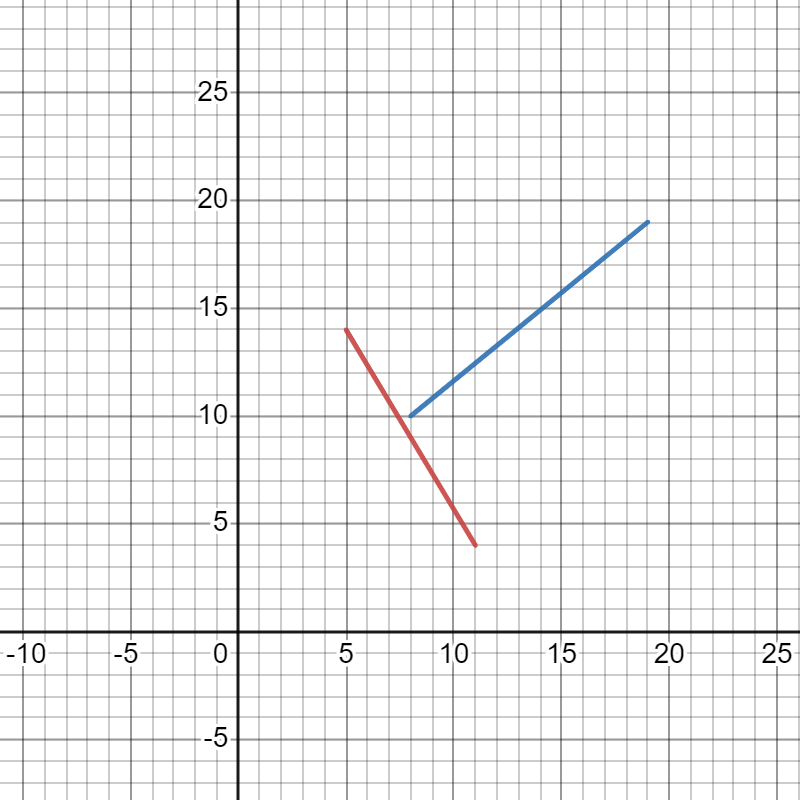
   (红色线段编号为1，蓝色线段编号为2。)
2. 查询与直线 $x=10$ 相交的线段中交点 $y$ 坐标最大的线段的编号。
   

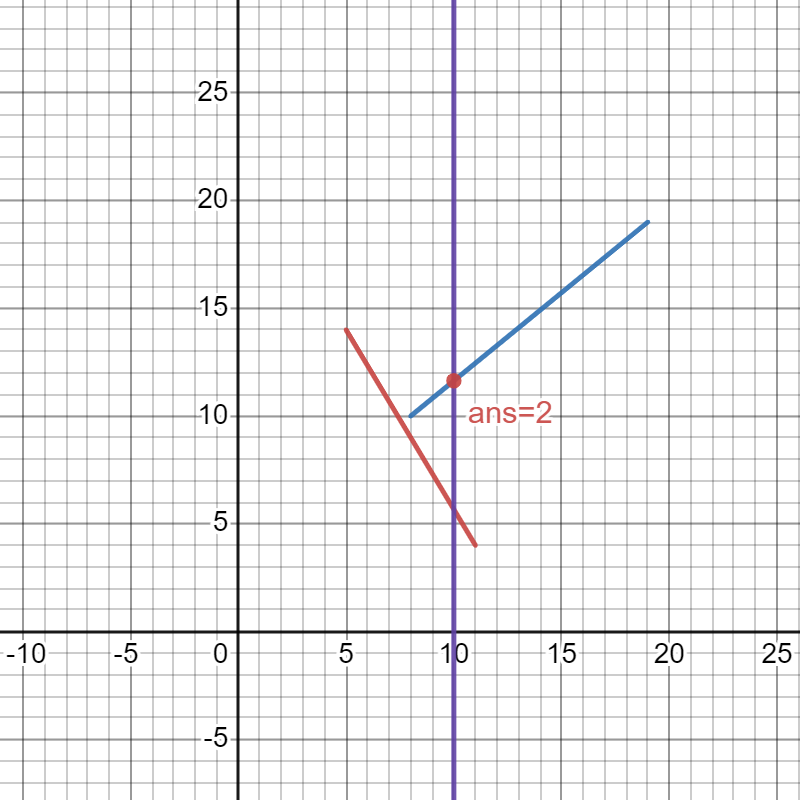
思路

首先，普通的线段树不容易直接维护答案，那我们就引入一种比普通线段树更高级的数据结构——李超线段树。

Q1:我们要维护什么？

A1:我们要维护该区间内在 $mid$ 处取值最大的线段，并认为它在整个区间内优势最大。

Ex

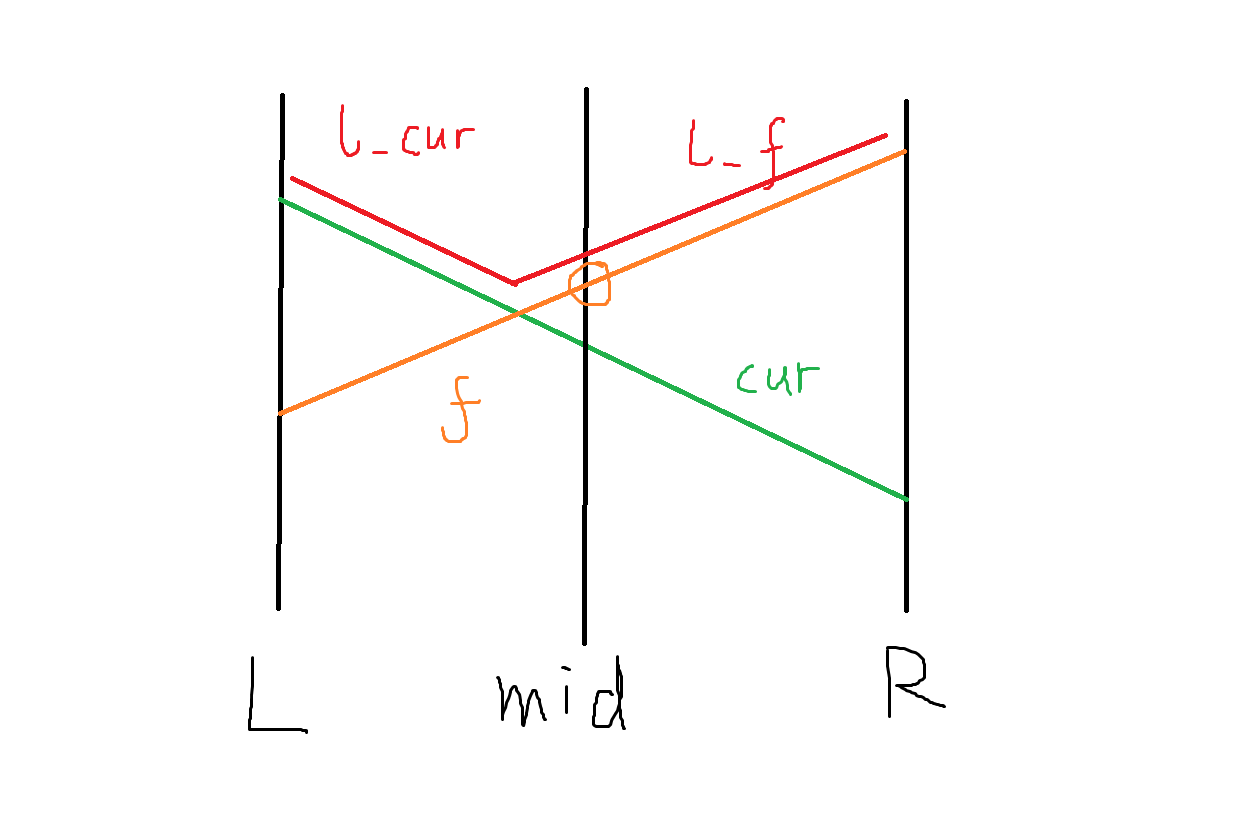
$$\tiny\color{grey}p.s.:我用鼠标写字的技术还是不错的$$
$cur$ 为之前的最优线段，$f$ 为要插入的线段，由于 $f$ 在 $mid$ 处的取值更优，所以显然，$l_f$ 的长度大于 $l_{cur}$，那么在区间 $[l,r]$ 中，$f$ 取到最大值的可能性更大。

Q2:插入操作是怎么实现的？

A2:我们要找到每一个需要更新的区间（注：是需要更新而不是可能被更新，因为需要被更新的节点可能有 $n$ 个，全部更新直接T飞，道理和普通线段树一样），并更新最优线段的编号。
（这里插入操作没有懒标记！）
那么如何确定一个区间可能被更新呢？
假设该区间已经被更新（$cur$ 和 $f$ 的值交换了），需要判断左半区间和右半区间需不需要更新：
1. 若 $cur$ 在左端点的取值小于 $f$，则左半区间需要进一步更新。
2. 反之，则左半区间不需要更新（因为 $cur$ 在左半区间绝对最优）。
3. 右半区间同理。

Ex：

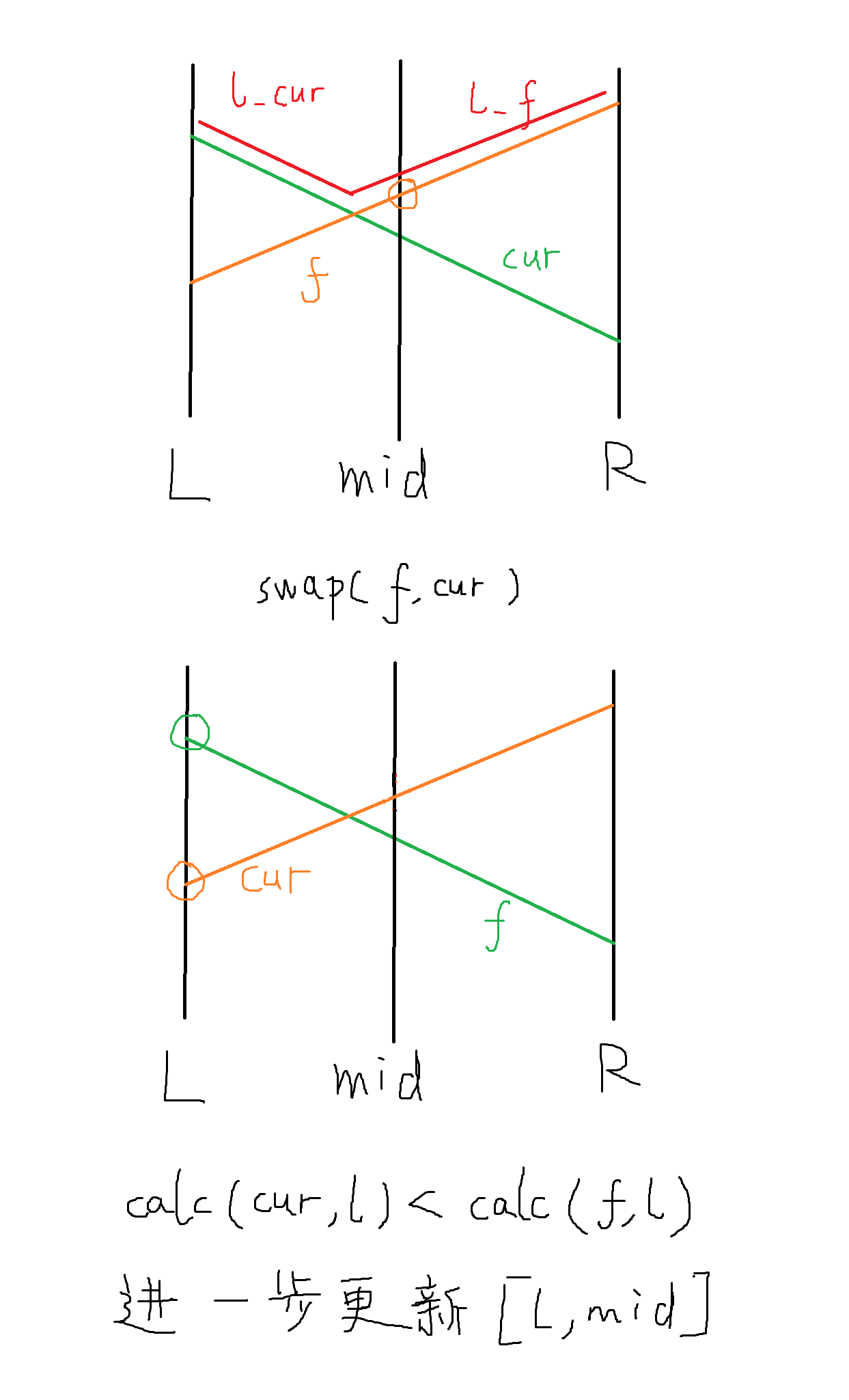
Q3:查询操作是怎么实现的？

A3:这个简单，找到所有包含 $k$ 的区间，取 $\begin{eqnarray} \min_{k\in [l,r]}\operatorname{calc}(best\text{_}segment([l,r]),k) \end{eqnarray}$，即所有包含 $k$ 的区间最优线段在 $k$ 处的最大值。

code:

#include<bits/stdc++.h>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
#include<map>
#include<unordered_map>
#include<set>
#include<list>
#define db double
#define inf 0x3f3f3f3f3f
#define INF 0x7f7f7f7f7f
using namespace std;
namespace Iwara{
    template<class T> T MAX(T x,T y){
        return x>y?x:y;
    }
    template<class T,class ... Arg> T MAX(T x,T y,Arg ... arg){
        return MAX(x>y?x:y,arg...);
    }
    template<class T> T MIN(T x,T y){
        return x<y?x:y;
    }
    template<class T,class ... Arg> T MIN(T x,T y,Arg ... arg){
        return MIN(x<y?x:y,arg...);
    }
    template<class T> T lowbit(T x){
        return x&-x;
    }
    template<class T> void SWAP(T &x,T &y){
        T qwq;
        qwq=x;
        x=y;
        y=qwq;
        return;
    }
}
using namespace Iwara;
const int MAXN=1e5+5,MOD1=39989,MOD2=1e9;
int n,lastans=0;
struct line{
    db k=0,b=0;
};
line Line[MAXN];
int tot=0;
void add_line(db x0,db y0,db x1,db y1){
    tot++;
    if(x0==x1){
        Line[tot].k=0,Line[tot].b=MAX(y0,y1);
        return;
    }
    Line[tot].k=1.0*(y1-y0)/(x1-x0),Line[tot].b=y0-Line[tot].k*x0;
    return;
}
db calc(int id,db d){
    return Line[id].b+Line[id].k*d*1.0;
}
int s[MOD1<<2];
void update(int id,int L,int R,int UL,int UR,int f){
    if(UR<L||R<UL||L>R)return;
    int mid=(L+R)>>1;
    if(UL<=L&&R<=UR){
        if(calc(f,mid)>calc(s[id],mid))SWAP(s[id],f);
        if(calc(f,L)>calc(s[id],L))update(id<<1,L,mid,UL,UR,f);
        if(calc(f,R)>calc(s[id],R))update(id<<1|1,mid+1,R,UL,UR,f);
        return;
    }
    update(id<<1,L,mid,UL,UR,f);
    update((id<<1)+1,mid+1,R,UL,UR,f);
    return;
}
pair<db,int> p_max(pair<db,int> p1,pair<db,int> p2){
    return p1.first!=p2.first?(p1.first>p2.first?p1:p2):(p1.second<p2.second?p1:p2);
}
pair<db,int> query(int id,int L,int R,db d){
    if(d<L||d>R)return {0,0};
    int mid=(L+R)>>1;
    db res=calc(s[id],d);
    if(L==R)return {res,s[id]};
    return p_max({res,s[id]},p_max(query(id<<1,L,mid,d),query((id<<1)+1,mid+1,R,d)));
}
int main(){
    cin>>n;
    int op;
    db qwq,x0,x1,y0,y1;
    for(int i=1;i<=n;i++){
        cin>>op;
        if(op==0){
            cin>>qwq;
            qwq=(((int)(qwq)+lastans-1+MOD1)%MOD1+1);
            lastans=query(1,1,MOD1,qwq).second;
            cout<<lastans<<endl;
        }
        else{
            cin>>x0>>y0>>x1>>y1;
            x0=(((int)(x0)+lastans-1+MOD1)%MOD1+1);
            x1=(((int)(x1)+lastans-1+MOD1)%MOD1+1);
            y0=(((int)(y0)+lastans-1+MOD2)%MOD2+1);
            y1=(((int)(y1)+lastans-1+MOD2)%MOD2+1);
            if(x0>x1)swap(x0,x1),swap(y0,y1);
            add_line(x0,y0,x1,y1);
            update(1,1,MOD1,x0,x1,tot);
        }
    }
    return 0;
}

应用

还是，先引入例题：
[CEOI2017]Building Bridges
$\tiny\color{grey}据说这是Liu\text{_}kevin巨佬模拟赛的场切题，然而他不会李超树所以只写了个\mathcal{O}(n^2)的暴戾。$
这是一道明显到不能再明显的斜率优化dp，根据题意，状态转移方程不难推出：
$\begin{align} dp[i]=h[i]^2+s[i-1]+\min (dp[j]-2h[i]h[j]+h[j]^2-s[j]) \end{align}$（$sum$ 为 $w$ 的前缀和）。
$\tiny\color{grey}由于我想毒瘤一下大家，特意省掉了推导过程/xyx$
（这个不是普通的斜率优化。）
这样，我们可以把问题转换成：
1. 插入一条斜率为 $-2h[j]$，截距为 $dp[j]+h[j]^2-s[j]$ 的直线。
2. 查询所有直线中，$x=h[i]$ 能截到的最小值。

这样，就可以用李超线段树维护了。