P1228 地毯填补问题
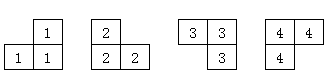
相传在一个古老的阿拉伯国家里，有一座宫殿。宫殿里有个四四方方的格子迷宫，国王选择驸马的方法非常特殊，也非常简单：公主就站在其中一个方格子上，只要谁能用地毯将除公主站立的地方外的所有地方盖上，美丽漂亮聪慧的公主就是他的人了。公主这一个方格不能用地毯盖住，毯子的形状有所规定，只能有四种选择（如图）：

并且每一方格只能用一层地毯，迷宫的大小为 $2^k$ * $2^k$ (0 < k <= 10)的方形。当然，也不能让公主无限制的在那儿等，对吧？由于你使用的是计算机，所以实现时间为1s

输入格式

第一行：k；

第二行：x,y，即给出公主所在方格的坐标（x 为行坐标，y 为列坐标），x 和 y 之间有一个空格隔开

输出格式

将迷宫填补完整的方案：每一补(行)为x\ y\ cx y c（x,yx,y 为毯子拐角的行坐标和列坐标， cc 为使用毯子的形状，具体见上面的图 11，毯子形状分别用 1,2,3,41,2,3,4 表示，x,y,cx,y,c 之间用一个空格隔开）。

输入样例

3 3 3

输出样例

5 5 1
2 2 4
1 1 4
1 4 3
4 1 2
4 4 1
2 7 3
1 5 4
1 8 3
3 6 3
4 8 1
7 2 2
5 1 4
6 3 2
8 1 2
8 4 1
7 7 1
6 6 1
5 8 3
8 5 2
8 8 1

说明

事实上感觉四个的形状分别是这样

此题使用递归分治的思想来做!!!!

假设 只有2 * 2:

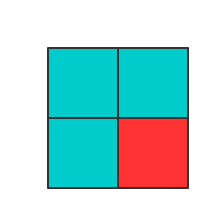
4 * 4 方格可以转化到 2 * 2的方格:

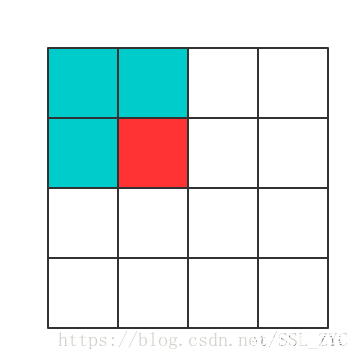
转化方法:在中间位置贴一个1号地毯:

在把贴的地毯当公主,这样就可以把没有公主的其它三个方向的所有方格铺面

再看 8 * 8的情况:
把中间点当成公主,铺一个合适的地毯.这样每个地毯所在的4*4的方格都有一个虚拟公主.

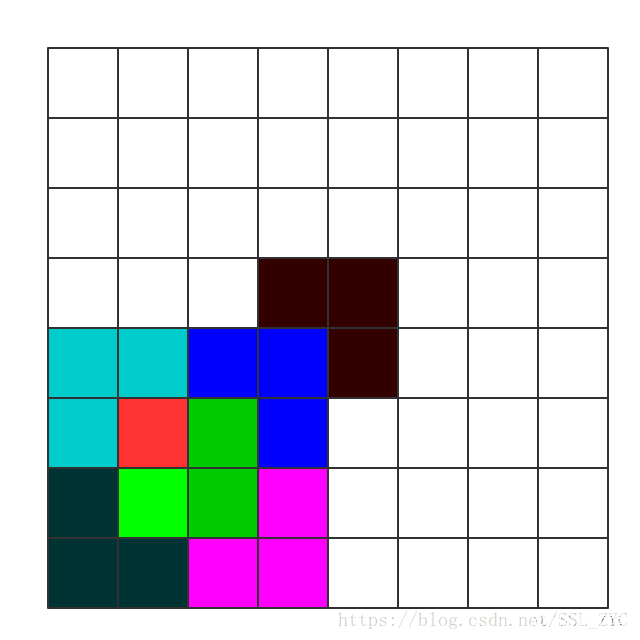
则按上面规则可以铺满所有的方格.

#include <iostream>

using namespace std;
#define leftup dfs(x1, y1, mid_x, mid_y, mid_x, mid_y); 
#define rightup dfs(x1, mid_y + 1, mid_x, y2, mid_x, mid_y + 1);
#define leftdown dfs(mid_x + 1, y1, x2, mid_y, mid_x + 1, mid_y);
#define rightdown dfs(mid_x + 1, mid_y + 1, x2, y2, mid_x + 1, mid_y + 1);
int x, y, k, n; // x, y 公主的坐标，k 2的次方数 
void dfs(int x1, int y1, int x2, int y2, int X, int Y){ // x1,y1:起点，x2, y2 :终点 ，X,Y 公主位置 

    if (x1==x2 && y1 == y2) return;// 终点和起点重合 
    //中点 
    int mid_x = (x2 - (x1 - 1)) / 2 + (x1 - 1); 
    int mid_y = (y2 - (y1 - 1)) / 2 + (y1 - 1);

    if (X <= mid_x && Y <= mid_y){ // 公主在中点的左上角 

        dfs(x1, y1, mid_x, mid_y, X, Y); // 左上角
        printf("%d %d 1\n", mid_x + 1, mid_y + 1); // 把中点当公主位置点， 用1号填补
        leftdown // 左下角     
        rightdown// 右下角
        rightup // 原公主的右上，这个点当公主继续填补 

    } else if (X <= mid_x && Y > mid_y){ // 右上角 

        dfs(x1, mid_y + 1, mid_x, y2, X, Y); // 右上角  
        printf("%d %d 2\n", mid_x + 1, mid_y);  // 2 号填补
        leftup// 左上角↖ 
        leftdown//左下 
        rightdown// 右下角 
    } else if (X > mid_x && Y <= mid_y){ // 左下 
        dfs(mid_x + 1, y1, x2, mid_y, X, Y);//左下角
        printf("%d %d 3\n", mid_x, mid_y + 1); // 左下 
        rightdown// 右下 
        leftup//左上
        rightup //右上 
    } else { // 右下 
        dfs(mid_x + 1, mid_y + 1, x2, y2, X, Y); // 右下 
        printf("%d %d 4\n",mid_x, mid_y);
        leftup//左上 
        rightup//右上
        leftdown//左下

    }
} 

int main() {
    cin >> k >> x >> y;
    n = 1 << k; // 方格的最大坐标
    dfs(1, 1, n, n, x, y);  

    return 0;
}