syf公式

syf公式又称两直线交点公式，它是利用两条直线上的任意四个点（每条直线各两个）来求解两直线交点坐标的算法公式。C++代码如下：

// (x,y)为两条直线的交点坐标
// 第一条直线上的点（(x1,y1),(x2,y2)）
// 第二条直线上的点（(x3,y3),(x4,y4)）
void syf(double &x, double &y, double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4)
{
    if (x1 == x2)
    {
        x = x1;
        y = (-x * (y4 - y3) - x4 * y3 + x3 * y4) / (x3 - x4);
        return;
    }
    else if (x3 == x4)
    {
        x = x3;
        y = (-x * (y2 - y1) - x2 * y1 + x1 * y2) / (x1 - x2);
        return;
    }
    else
    {
        double k1 = (y2 - y1) / (x2 - x1);
        double k2 = (y4 - y3) / (x4 - x3);
        double b1 = y1 - k1 * x1;
        double b2 = y3 - k2 * x3;
        if (y1 == y2)
        {
            y = y1;
            x = (y - b2) / k2;
            return;
        }
        if (y3 == y4)
        {
            y = y3;
            x = (y - b1) / k1;
            return;
        }
        x = (b2 - b1) / (k1 - k2);
        y = k1 * x + b1;
        return;
    }
}

公式推导

由于我们只知道每条直线上的任意两点坐标，故应用直线的两点式方程是比较好的选择。

由于题目保证两条直线会存在交点，故根据横坐标可分为三种情况：
①x1==x2 && x3!=x4
②x3==x4 && x1!=x2
③x1!=x2 && x3!=x4

对于①和②，我们已经清楚了交点的横坐标，直接代入两点式公式即可。

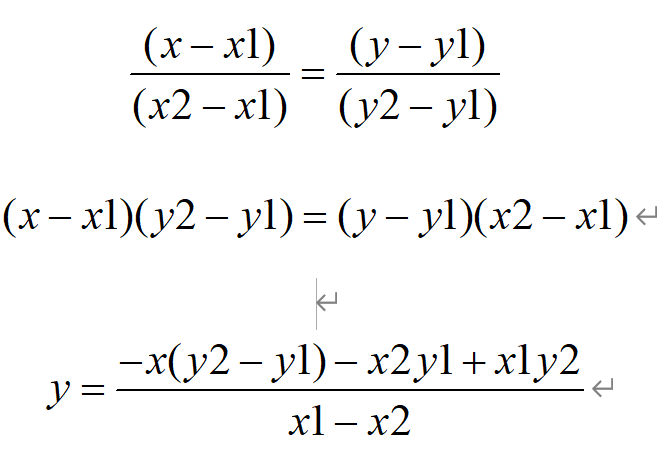
接下来我们来分析③
这种情况的两条直线不满足垂直于x轴，故我们可以使用直线的斜截式方程。

于是我们又可以细分纵坐标的情况
①y1==y2 && y3!=y4
②y3==y4 && y1!=y2
③y1!=y2 && y3!=y4

对于①和②，我们确定了交点的纵坐标，故代入斜截式方程可求。

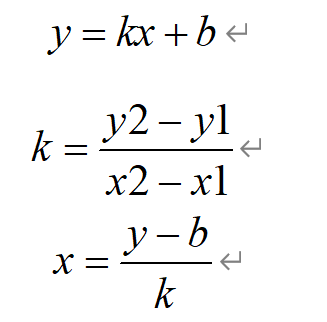
而对于③，我们一般推导即可。

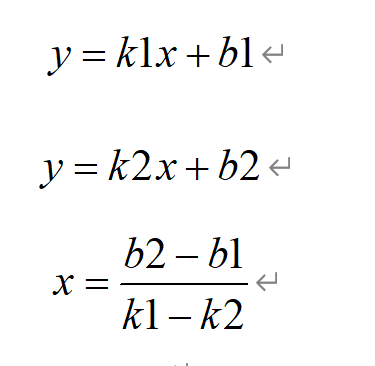
sxy同学改进版

void syf_sxy(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4)
{
    double x = (x1 * y2 - x2 * y1) * (x3 - x4) - (x3 * y4 - x4 * y3) * (x1 - x2);
    x /= (x1 - x2) * (y3 - y4) - (x3 - x4) * (y1 - y2);
    double y = (x1 * y2 - x2 * y1) * (y3 - y4) - (x3 * y4 - x4 * y3) * (y1 - y2);
    y /= (x1 - x2) * (y3 - y4) - (x3 - x4) * (y1 - y2);
}