Trie

高效地存储和查找字符串集合的数据结构

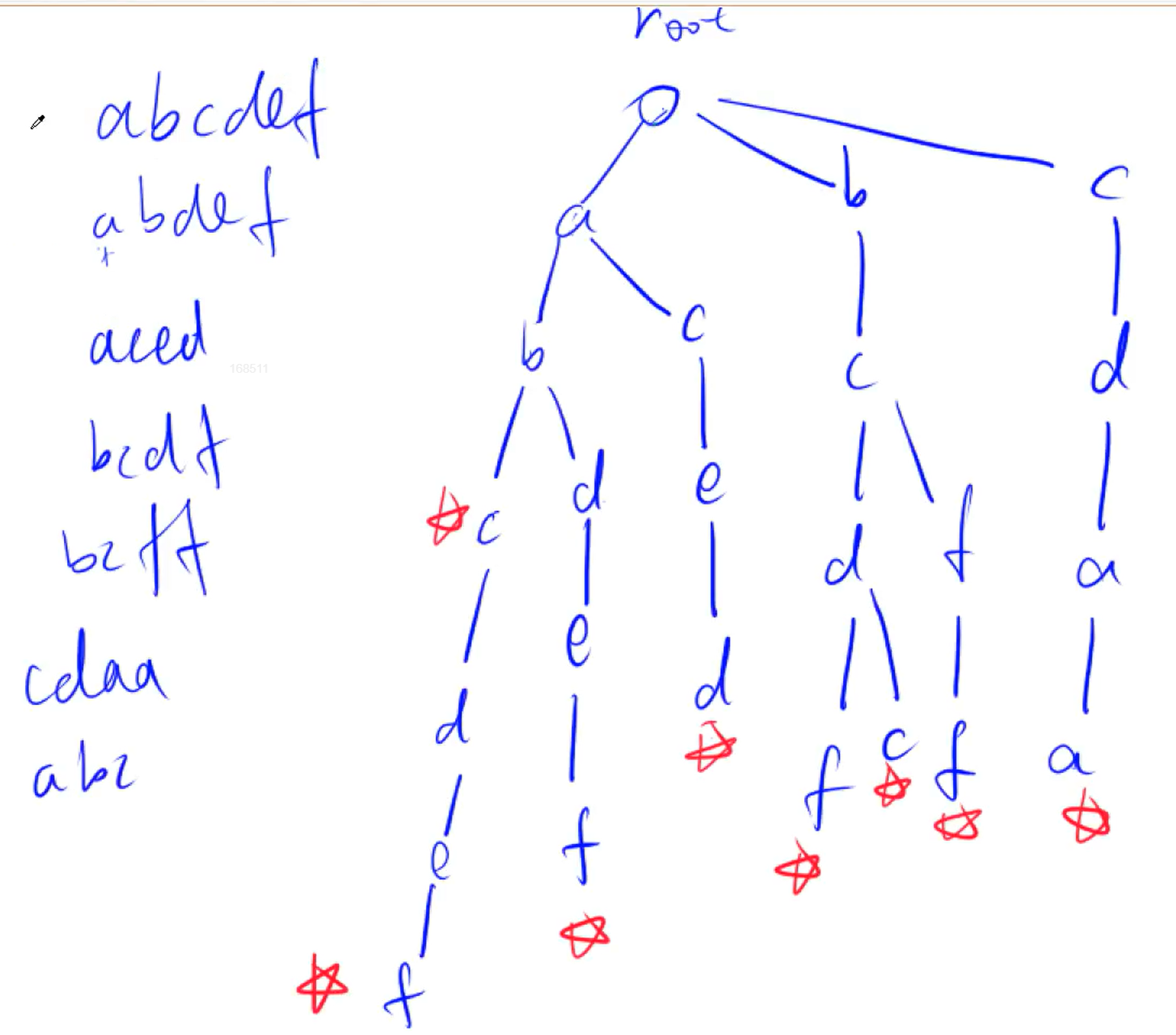
• “高效”体现在Trie存储了公共的前缀。

Trie树的模板

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int son[N][26];    //son[i][j]表示第i个节点的a~z儿子是否存在(0表示不存在)，且是第几个节点，因为全是小写字母，所以一个节点最多26个儿子
int idx;  //和单链表里的idx是一个东西，表示"第几个"节点，第0个节点既是空节点也是根节点
int cnt[N];  //cnt[i]表示以第i个节点结尾的单词有多少个

//在Trie树中插入字符串
void insert(char str[])
{
    int p = 0;  //从根节点（第0个节点）开始，p的作用类似指针，指向当前节点
    for(int i = 0;str[i];i++)
    {
        int u = str[i] - 'a';  //获取字母的“代号”，0~25分别表示a~z

        //比如字母"c"的u是2，那么son[p][2]就是表示"c"是否是第p个节点的儿子
        //若c不是第p个节点的儿子，那表示没有存储这个前缀，就自己开拓一个分支
        //idx++即创建一个新节点
        if(!son[p][u]) son[p][u] = ++idx;  
        //创建一个新节点的时候会分配一个新的idx
        //表示第p个节点的字母“c”这个儿子有了，并且是第++idx个节点

        p = son[p][u];  //往下走，研究下一个节点。
    }

    cnt[p] ++;  //结束循环后，cnt[p]++，表示以第p个节点作为结尾的单词数+1
}

//查找某个字符串出现了多少次
int query(char str[])
{
    int p = 0;
    for(int i = 0;str[i];i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;  //一路往下找，要找某个字母的时候发现前一个字母没有这个儿子，即没有这个单词
        p = son[p][u];
    }
    //若在for循环内对要查找的单词每个字母都能找到已有前缀节点，则跳出循环执行这句
    return cnt[p];

}

并查集

1. 将两个没有相交元素的集合合并
2. 询问某两个元素是否在一个集合中

基本原理

• 每个集合用一棵树表示，树根节点root的编号就是当前这个集合的编号。对于每一个节点，都存储它的父节点是谁（p[x]表示x的父节点）；当想求某个点属于哪个集合的时候，先找它的father，直到找到树根，树根的编号就是当前这个节点属于的集合编号。
• 如何判断树根：p[x] == x （x的父节点就是x自己，那么x就是根节点）
• 如何求x的集合编号：while(p[x]!=x) x = p[x] （只要x不是树根，就继续往上走） 跳出循环时的x就是根节点的编号即集合编号
• 如何合并两个集合：把一个集合的根节点当做另一个集合的根节点的儿子。比如，px是x集合的编号，即x集合这棵树的根节点的编号，py是y的集合编号。p[x] = y，即x集合的树根的父亲节点是y集合的树根。

求某个节点属于哪个集合这一步的时间复杂度还可以得到优化：路径压缩

• 当某个节点一路往上爬，找到了根节点，确定了自己属于哪个集合之后，直接把经过路径上的所有节点的父节点直接设为根节点，即将这些节点直接指向根节点。这样以后求这些节点属于哪个集合的时候，往上爬只需要爬一步就到根节点了，就可以确定自己属于哪个集合了。

模板题原题链接

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int p[N];   //father数组，存储每个元素的父节点是谁

int n,m;

int find(int x) //返回x所在集合的编号（祖宗节点的编号） + 路径压缩优化
{
    if (p[x]!=x)  //x不是根节点
    {
        p[x] = find(p[x]);  //往上走调用x的父节点，直接把祖宗节点作为路径上每一个节点的父节点
    }
    return p[x];
}

int main()
{
    cin>>n>>m;
    for(int i = 1;i<=n;i++) p[i] = i;  //一开始n个数，分别是n个集合，初始化树根。

    while(m--)
    {
        char op;
        int a,b;
        cin>>op>>a>>b;

        if(op == 'M')  //合并两个集合
        {
            p[find(a)] = find(b);  //b集合根节点作为a集合根节点的父亲
        //若ab已经在同一集合，find(a)==find(b)，即p[x]=x(根节点的定义)，即直接忽略此操作
        }
        else if(op=='Q')  //查询两个节点是否在一个集合中
        {
            if(find(a)==find(b)) puts("Yes");
            else puts("No");
        }

    }
    return 0;
}

并查集的核心就是这个find函数，其他都是可以自己推的

int find(int x) //返回x所在集合的编号（祖宗节点的编号） + 路径压缩优化
{
    if (p[x]!=x)  //x不是根节点
    {
        p[x] = find(p[x]);  //往上走调用x的父节点，直接把祖宗节点作为路径上每一个节点的父节点
    }
    return p[x];
}

堆（手写）

• 堆是完全二叉树。
• 小根堆：每个点都小于等于左右儿子，即根节点是最小值
• 存储堆数据结构的方式：用一维数组。 x的左二子：2x；右儿子：2x+1

基本操作：

1. 插入一个数
2. 求集合中的最小值
3. 删除最小值
4. 删除任意一个元素
5. 修改任意一个元素

其中前三个操作是STL可以直接实现的，后面两个是STL不能直接实现的
这五个基本操作，都可以用两个函数：donw(x)和up(x)组合起来

具体实现；

• 插入一个数x，就是在一维数组的最后插入x：heap[++size] = x，再把x不断用up(x)往上移

• 求集合中的最小值：即堆顶元素heap[1]

• 删除最小值：用整个堆的最后一个元素heap[1] = heap[size]，覆盖堆顶元素，然后size--，再把新堆顶元素往下移down(1)

• 删除任意一个元素：同理，heap[k] = heap[size]，size--,然后看看是down还是up

• 修改任意一个元素：heap[k] = x，看看是down还是up

down和up操作

void down(int u) //每次看要不要down，就是看该点是否小于他的左右儿子
{
    int t = u;  //用t来表示他自己、和他左右儿子这三个节点中的最小节点的编号

    if(2*u<=cnt && h[2*u]<h[t]) t = 2*u;   //左儿子是最小节点。2*u<=cnt是用来判断它是否有左儿子
    if(2*u+1<=cnt && h[2*u+1]<h[t]) t = 2*u+1;   //左儿子是最小节点

    if(u!=t)
    {
        swap(h[u],h[t]);  //交换值，没交换序号
        down(t);   //第u个节点被换到第t个节点的位置了，递归调用，继续down
    }
}

void up(int u)
{
    while(u/2 >= 1 &&h[u]<h[u/2])  //有父节点，且父节点比我大
    {
        swap(h[u/2],h[u]);
        u /= 2;
    }
}