本部分是树上dp的习题讲解 基础知识见 树形dp知识全解
本章涉及的题单
树形dp
1. P1122 最大子树和 枚举每个点的最长路径权值和
2. 1072. 树的最长路径 枚举每个点的最长路次长路求和即可
3. 1075. 数字转换 对本题的关系建树 最后转化为最长路径问题
4. P2796 Facer的程序 分布乘法 转化为分别计算不同子树下的子树大小成绩
5. P1131 [ZJOI2007] 时态同步 简易的树上dp问题 修改在根节点位置处修改即可
6. 285. 没有上司的舞会
7. 323. 战略游戏 本题是对于边的判断 对每一条边的状态只有强制选与不选两种
8. 1077. 皇宫看守 本题是对于点的判断 所以定义三维转态
9. P4395 [BOI2003]Gem 气垫车 暴力枚举点的可选权值判断换根dp
1. 1073. 树的中心 换根dp入门
2. P3478 [POI2008] STA-Station 换根dp 处理某个点到其余每个节点深度和最小
$\space\space\space$ 2.1 (此处与上题思路类似 不再讲解)
$\space\space\space$ P2986 [USACO10MAR] Great Cow Gathering G
$\space\space\space$ CF1187E Tree Painting
$\space\space\space$ P1364 医院设置
3. 4381. 翻转树边 换根dp 每个边的贡献仅为1次
4. P3047 [USACO12FEB]Nearby Cows G
5. CF708C Centroids
6. P6419 [COCI2014-2015#1] Kamp树上分组背包
1. 1074. 二叉苹果树
2. P1273 有线电视网
3. P2014 [CTSC1997] 选课
4. P3698 [CQOI2017]小Q的棋盘
5. P3177 [HAOI2015] 树上染色
6. CF815C Karen and Supermarket
一 树形dp
1.1 P1122 最大子树和
题意
$\space\space\space\space\space$ 给定一个带有边权的子树 选择其中最大的子树 使得该子树的权值和最大
分析
$\space\space\space\space\space$ 从贪心的角度出发 要使剩余的子树权值和最大 则对每一个子节点枚举 如果该子树的权值和 $\geq$ 0 我们就选取进行累加即可
源码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e5 + 1e2, INF = 0x3f3f3f3f;
typedef long long LL;
#define int long long
int n;
int h[N], e[N], ne[N], w[N], idx;
int ans;
int f[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int father)
{
f[u] = w[u];
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(j == father) continue;
dfs(j, u);
if(f[j] > 0) f[u] += f[j]; //自底向上 用子节点更新父节点信息
}
}
signed main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 1; i <= n; i ++) cin >> w[i];
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs(1, -1);
int res = - INF;
for(int i = 1; i <= n; i ++) res = max(res, f[i]);
cout << res << endl;
}
1.2 1072. 树的最长路径
题意
$\space\space\space\space\space$ 找到一条路径,使得使得路径两端的点的距离最远
分析
$\space\space\space\space\space$ 我们先看下这个路径的组成 对于一条路径的最值 我们要么枚举一个端点 进而判断另一个最值的端点 要么就枚举其中的点 枚举该点到两个端点的距离 找到距离最远的两个端点 前者本文不在赘述 我们讲讲后者做法 我们发现 如果我们枚举一条路径的中间点 进而找到距离两个端点的最远距离进行求和 便恰好将最远的路径给不断地更新出来 进而我们对每个点进行枚举 找到距离的最值d1 次大值d2不断维护两个最值即可
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 2e4 + 10;
int h[N], e[N], ne[N], w[N], idx;
int f[N][N];
int d1[N], d2[N]; // d1 d2 记录以u为根节点的最长距离 次长距离
int n, m;
int ans;
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
int t = d1[v] + w[i];
if(t >= d1[u]) d2[u] = d1[u], d1[u] = t;
else if(t > d2[u]) d2[u] = t;
}
ans = max(ans, d1[u] + d2[u]);
}
int main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i < n; i ++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << ans << endl;
}
1.3 1075. 数字转换
题意
$\space\space\space\space\space$ 给定一个范围 求这个范围能进行 数字变化且不出现重复变换的最多的个数是多少个
分析
$\space\space\space\space\space$ 对于每次的变换我们可以通过暴力枚举进行完成所有的变换操作 而对于其中最长的一个变换路径 我们发现 当我们对变换进行树的构建的时候 最长的变换路径就是树的最长直径 另外需要注意的是 对于建边的枚举 我们直接暴力枚举显然会T 所以我们是通过倍数枚举进行排除冗余的判断 其次的注意在我们的建图中 我们是人为给建边定义一个从根节点到叶子节点的方向 所以我们只需要建立单向边即可
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int h[N], e[N], ne[N], idx;
int d1[N], d2[N];
int n, fsum[N];
int res;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{
if(d1[u]) return;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
dfs(v);
int dist = d1[v] + 1;
if(dist >= d1[u]) d2[u] = d1[u], d1[u] = dist;
else if(dist > d2[u]) d2[u] = dist;
}
res = max(res, d1[u] + d2[u]);
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 1; i <= n; i ++) //倍数枚举
for(int j = 2; j <= n / i; j ++)
fsum[i * j] += i;
for(int i = 2; i <= n; i ++) //如果符合关系 则建立一条边连接
if(fsum[i] < i) add(fsum[i], i);
for(int i = 1; i <= n; i ++) dfs(i);
cout << res << endl;
}
1.4 P2796 Facer的程序
题意
$\space\space\space\space\space$ 给定一个树 求有多少个子树满足形成的树的顺序是满足根节点->叶子节点有序的
分析
$\space\space\space\space\space$ 对一个节点u分析 它的每个儿子节点v 从u -> v 不管v是选择一个 还是两个还是 sz[v]个 只要满足$v_1, v_2.... v _{sz[v]}$ 的顺序无论如何选择都是有序的 所以对每个节点v的选择方式有 sz[v] + 1(1是不选)个情况 又因为只要按照从根节点出发遍历的顺序 节点与节点的选择方式是互不干涉的 即分布乘法 进而求解运算即可
源码
#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int N = 2e5 + 10, mod = 1e9 + 7;
int h[N], e[N], ne[N], idx;
int sum[N];
int n;
bool not_root[N];
int ans;
int f[N]; //f[u] 代表以u为根节点的子树的符合题意的方案数
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int father)
{
f[u] = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
f[u] = f[u] *(f[v] + 1) % mod; //计算 以u为节点的方案个数 分布乘法 可能不止一个子树
}
ans = (ans + f[u]) % mod;//统计求和
}
signed main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
not_root[b] = true;
}
int root = 1;
while(not_root[root]) root ++; //根节点不明 手动找根节点
dfs(root, -1);
cout << ans << endl;
}
1.5 P1131 [ZJOI2007] 时态同步
题意
$\space\space\space\space\space$ 我们将从根节点同时到所有叶子结点(每个路径的时间代价均为1)称为时态同步 而在任意一个树中 我们可以人为的将某个路径的代价+ 1 进而让你求得 给定的任意树 达成时态同步的最少代价是多少
分析
$\space\space\space\space\space$ 我们发现在所有的路径中 最长的一个路径最为标准存在 其余的到叶子结点的子树则都需要进行更改 而从贪心的角度出发 对于有多个子节点v的父亲节点u 显然在根节点处进行修改的代价更优(根节点的修改可以使得整个数中的众多子树都更改且代价仅为1) 所以我们的方案是 自底向上枚举 枚举到所含多个叶子节点的父节点处 进行修改 使得该节点的众多子树到达叶子节点的时间均相同进而进行下一个父节点的枚举
源码
#include<iostream>
#include<cstring>
#include<algorithm>
#define int long long
#define endl '\n'
using namespace std;
const int N = 5e5 + 10, M = N * 2;
int sz[M];
int n, m;
int e[M], ne[M], h[M], w[M], idx;
int d[N];
bool st[M];
int ans;
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
d[u] = max(d[u], d[v] + w[i]); //更新每个父节点的代价最值
}
for(int i = h[u]; i != -1; i = ne[i]) //对同属于一个父节点的所有子树遍历完后 开始计算代价
{
int v = e[i];
if(v == father) continue;
ans += d[u] - (d[v] + w[i]); //如果不是更新最值的来源的v子树 就计算代价
}
}
signed main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(m, -1);
cout << ans << endl;
}
1.6 285. 没有上司的舞会
题意
$\space\space\space\space\space$ 给定一棵树 子节点跟父节点只能同时选择一个 求所选择的方案中权值最大的一个
分析
$\space\space\space\space\space$ 自顶向上遍历每个节点 分别记录在该点选与不选的方案中的最值
定义f[u][0 / 1] 表示u这个节点选与不选的方案权值集合 0 表示该点不选 1表示选
f[u][0] += f[v][1]; //父节点不选 子节点必须选
f[u][1] += min(f[v][0], f[v][1]); //父节点选 则子节点选与不选都可 更新最少的一个
源码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 6010;
int f[N][2], happy[N];
int e[N], ne[N], h[N], idx;
bool has_fa[N];
int n;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{
if(f[u][1]) return;
f[u][1] = happy[u];
for(int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
dfs(v);
f[u][1] += f[v][0];
f[u][0] += max(f[v][0], f[v][1]);
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++) cin >> happy[i];
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; i ++)
{
int a, b;
cin >> a >> b;
add(b, a);
has_fa[a] = true;
}
int root = 1;
while(has_fa[root]) root ++;
dfs(root);
cout << max(f[root][0], f[root][1]);
return 0;
}
1.7 323. 战略游戏
题意
$\space\space\space\space\space$ 给定一个树 每个树的每条边必须放置一个哨兵 求怎样放置使得所需的哨兵数量最少
分析
$\space\space\space\space\space$ 本题是边强制问题 我们对每一个边进行抉择 发现仅仅只有选与不选两种 那么我们给这两个情况进行分别判断 进而转化为没有上司的舞会一题
f[u][0] += f[v][1]; //父节点不选 子节点必须选
f[u][1] += min(f[v][0], f[v][1]); //父节点选 则子节点选与不选都可 更新最少的一个
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1510;
int n;
int h[N], e[N], ne[N], idx;
int f[N][2];
bool not_root[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{
f[u][0] = 0, f[u][1] = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
dfs(v);
f[u][0] += f[v][1];
f[u][1] += min(f[v][0], f[v][1]);
}
}
int main()
{
while(~scanf("%d", &n))
{
memset(h, -1, sizeof h); idx = 0;
memset(not_root, 0, sizeof not_root);
for(int i = 0; i < n; i ++)
{
int a, b, Size;
scanf("%d:(%d)", &a, &Size);
while(Size --)
{
cin >> b;
add(a, b);
not_root[b] = true;
}
}
int root = 0;
while(not_root[root]) root ++;
dfs(root);
cout << min(f[root][0], f[root][1]) << endl;
}
return 0;
}
1.81077. 皇宫看守
题意
$\space\space\space\space\space$ 与上题不同的是 本题是每两个相邻的节点必须选择一个 进而判断选取方案中代价最少的一个方案
分析
$\space\space\space\space\space$ 我们先来看下与上题的不同之处
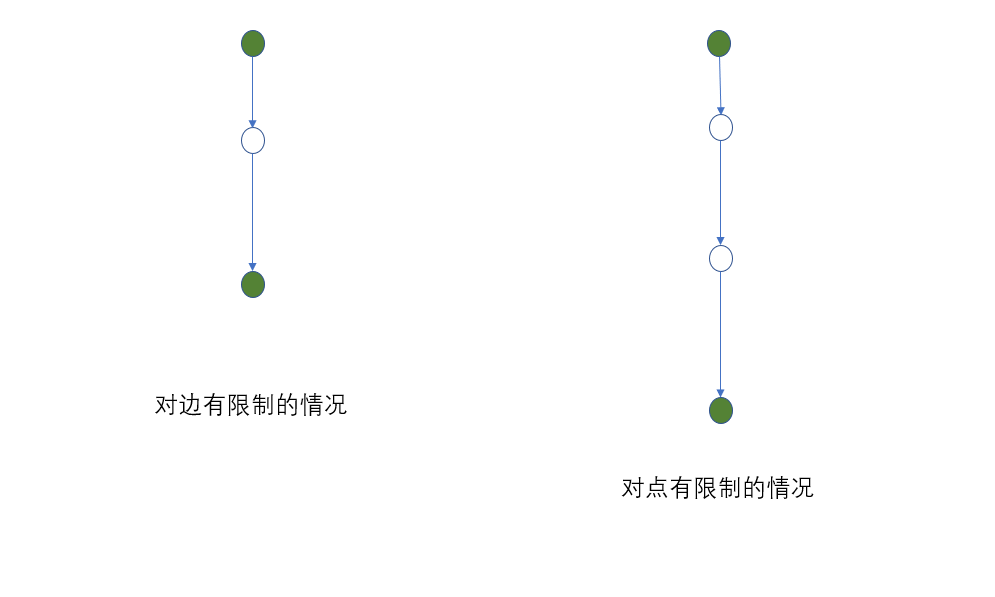
$\space\space\space\space\space$ 我们发现 对边的限制下 我们的边强制只有两个转态 选与不选 而对于点的限制 我们显然不能等同于边的情况 因为如图我们可能是相连的两个点 可能分别由其的父节点与子节点看到 致使这两个点虽属于同一条边 但该边并无任何选择 所以我们不能用上题的思路解释 不过本题中 我们对状态判读 发现最多仅仅三种状态
f[u][0] 代表被u的父节点看到
f[u][1] 代表被u的子节点看到
f[u][2] 代表u自己放置守卫
$\space\space\space\space\space$ 而我们对状态定义好了 进行状态转移
v 是 u的子节点
f[u][0] 被u点的父节点看到 f[u][1] = 被u点的子节点看到 f[u][2] = 自己放置守卫
f[u][0] = min(f[v][1], f[v][2]) // 如果 u是由父节点看到 那么子节点要合法 要么是由v的子节点看到 要么就是自己放置守卫
f[u][2] = min(f[v][0], f[v][1], f[v][2]) + w[u] //如果u是由自己放置 那么对于v的所有选择均合法 w[u]是在u点放置守卫的数量
f[u][1] = min(f[v][1], f[v][2]) if(选择的全是f[v][1]) 则在加上 min(f[v][2], f[v][1])
表示节点u是被自己的子节点观察到的 那么我们分析 观察的前提是需要满足以v为根节点的子树的状态是合法的
(dp是一种拓扑序 在状态被定义的时候 顺序就已经确定了 对于顺序的实现 要么自顶向下 要么自底向上 前者for循环 后者就是树上递归 而状态转移的设定
代表着 在枚举下一个点的时候 上一个点时候的状态结果已经被求出(不合法的标记INF 计算直接排除)) 所以这就是前面min(f[v][1], f[v][2])的由来
其次 根据我们的状态 我们是在每次枚举一个点的时候 就将当前子节点的合法状态记录总和 如果对所有的子节点求和的时候均是由字节点的子节点看到的话
即所有u的子节点没有一个选择的 那么要是满足u是由子节点看到 我们必须满足U的其中一个子节点必须将状态从f[v][1] -> f[v][2](从被子节点看到 -> 自己放置守卫看到子节点和u节点)
只有这样 才能存在一个子节点观察到u节点 所以我们必须对其中一个子节点进行决策转移 显然进行决策转移只需要一个就行 而且这一个一定是决策侧的代价最少的一个 进行决策的代价是什么
就是f[v][2] - f[v][1] (类似于补差价) 进而判断即可
源码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1510, INF = 1e9;
int n;
int h[N], w[N], e[N], ne[N], idx;
int f[N][3];// 0 父 1 子 2自己
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u)
{
f[u][2] = w[u];
//sum记录子节点有多少个是选择u的子节点放置 而不是由u的子节点的子节点观察到u的子节点
int sum = 0, cost_min = INF; //cost_min 记录差价
for (int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
dfs(v);
f[u][0] += min(f[v][1], f[v][2]); //
f[u][2] += min(min(f[v][0], f[v][1]), f[v][2]);
if(f[v][2] < f[v][1]) sum ++; //记录U的子节点放置的个数
else cost_min = min(cost_min, f[v][2] - f[v][1]); //记录差价
f[u][1] += min(f[v][1], f[v][2]);//合法的v的状态转移
}
if(!sum) f[u][1] += cost_min; //如果u的子节点均是由u的子节点的子节点观察 则必须选择一个最小的进行差价弥补
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ )
{
int id, cost, cnt;
cin >> id >> cost >> cnt;
w[id] = cost;
while (cnt -- )
{
int ver;
cin >> ver;
add(id, ver);
st[ver] = true;
}
}
int root = 1;
while (st[root]) root ++ ;
dfs(root);
cout << min(f[root][1], f[root][2]) << endl;
return 0;
}
1.9P4395 [BOI2003]Gem 气垫车
题意
$\space\space\space\space\space$ 给定一棵树 树的相邻两个节点不能选择相同的权值 权值从1开始选择 问如何选择 使得整个子树的权值和最小
分析
$\space\space\space\space\space$ 首先 我们可以考虑到12交替染色的贪心思路是错的 如下图
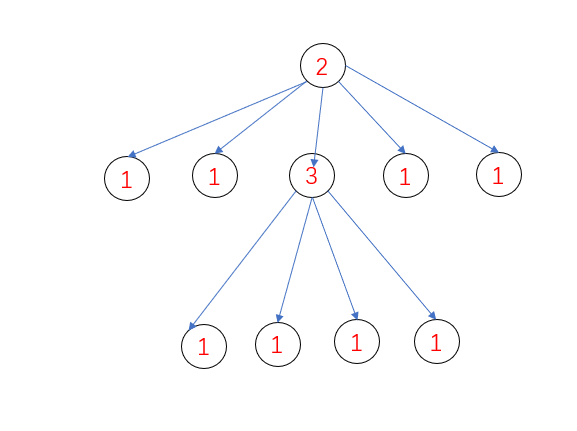
所以我们不能简易的通过交替染色进行判断 我们讨论最坏情况下的染色 我们发现这个能选举颜色的范围是有上限的 四色定理 所以我们对每个点进行枚举所有的状态 我们定义f[u][k]表示第u个节点选择k染色的方案 最后输出 for k 1 -> 4 min(f[u][k])即可 本题的状态是最小值的恰好问题 对状态的初始化需要设置为极值 详见初始化见背包问题全解
源码
#include<iostream>
#include<cstring>
#include<algorithm>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e5, INF = 1e18;
int f[N][20];
int sz[N];
int n, m;
int e[N], ne[N], h[N], w[N], idx;
int a[N], b[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int father)
{
for(int i = 1; i <= 4; i ++) f[u][i] = i; //状态初始化赋值
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
for(int j = 1; j <= 4; j ++) //枚举父节点的选择
{
int minn = INF;
for(int k = 1; k <= 4; k ++) //不同颜色的子节点更新父节点
{
if(j != k) minn = min(minn, f[v][k]);
}
f[u][j] += minn;
}
}
}
signed main()
{
cin >> n;
memset(f, 0x3f3f3f3f, sizeof f); //本题是最小值的恰好问题 所以对状态的更新需要先设置成INF
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs(1 ,-1);
int minn = INF;
for(int i = 1; i <= 4; i ++) minn = min(minn, f[1][i]);
cout << minn << endl;
}
二. 换根dp
2.1 1073. 树的中心
题意
$\space\space\space\space\space$ 给定一棵树 在树上找到一个点 使得该点到其他点的最远距离最近
分析
$\space\space\space\space\space$ 我们很容易联系到最长路径哪题 不过我们发现 如果使用简单的树形dp只能仅仅枚举到子节点的所有情况(树的遍历导致)而不能枚举到由父节点转移的所有情况(可以暴力枚举每个点作为根节点的情况进行更新 不过枚举所有点 显然容易T) 所以我们需要在进行一次dfs来更新父节点对子节点的操作局限 在第一次遍历时候 预处理出每个点的最长路和次长路 以及次长路的转移节点 然后再第二次的遍历时候 进行更新即可
$\space\space\space\space\space$ 其次为什么要设置次短路? 根据递归的性质 我们每次递归更新父节点的时候 子节点都是不同的 换句话说 就是最长路跟次长路所对应的子节点是不同的 我们记录下 最长路的出发子节点 判断进行更新 每个节点向下的最长节点 是子节点更新父节点 那么我们直接递归然后再更新即可 然而 向上则是用父节点的信息 更新子节点 所以直接先更新 在递归处理 期间注意最长路的判断更新即可
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 2e4 + 10, INF = 0x3f3f3f3f;
int h[N], w[N], e[N], ne[N], idx;
int d1[N], d2[N], pre[N], up[N]; //pre 记录该点是从哪个点转移来的
//为什么要设置次短路 根据递归的性质 我们每次递归更新父节点的时候 子节点都是不同的
//换句话说 就是最长路跟次长路所对应的子节点是不同的 我们记录下 最长路的出发子节点 判断进行更新
//每个节点向下的最长节点 是子节点更新父节点 那么我们直接递归然后再更新即可
//然而 向上则是用父节点的信息 更新子节点 所以直接先更新 在递归处理 期间注意最长路的判断更新即可
int n;
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
int dfs_d(int u, int father)//预处理以u为节点的最大值 和次大值(在求上方最长时 避免产生冲突)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(j == father) continue;
int t = dfs_d(j, u) + w[i];
if(t >= d1[u])
{
d2[u] = d1[u], d1[u] = t;
pre[u] = j;
}
else if(t > d2[u]) d2[u] = t;
}
return d1[u];
}
void dfs_u(int u, int father)//求该点的父节点方向的最大值 === 父节点的最长距离 + w[i] 如果最长路就是经过j的点 就用次大值更新
{
for(int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if(j == father) continue;
if(pre[u] == j) up[j] = max(up[u], d2[u]) + w[i];
else up[j] = max(d1[u], up[u]) + w[i];
dfs_u(j, u);
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i <= n; i ++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs_d(1, -1), dfs_u(1, -1);
int res = INF;
for(int i = 1; i <= n; i ++) res = min(res, max(d1[i], up[i]));
cout <<res <<endl;
}
2.2 P3478 [POI2008] STA-Station
题意
$\space\space\space\space\space$ 给定一棵树 选择一个节点 使得其余的所有点到这个点的路径之和最大
分析
$\space\space\space\space\space$ 考虑换根dp
f[u] 表示整棵树到u点的距离之和
g[u] 表示以u为根节点的子树到u的距离之和
sz[u] 表示以u为根节点的子树的大小之和
对于从u - > v的状态转移 f[v] = f[u] - 2 * g[v] + g[1]
见图解
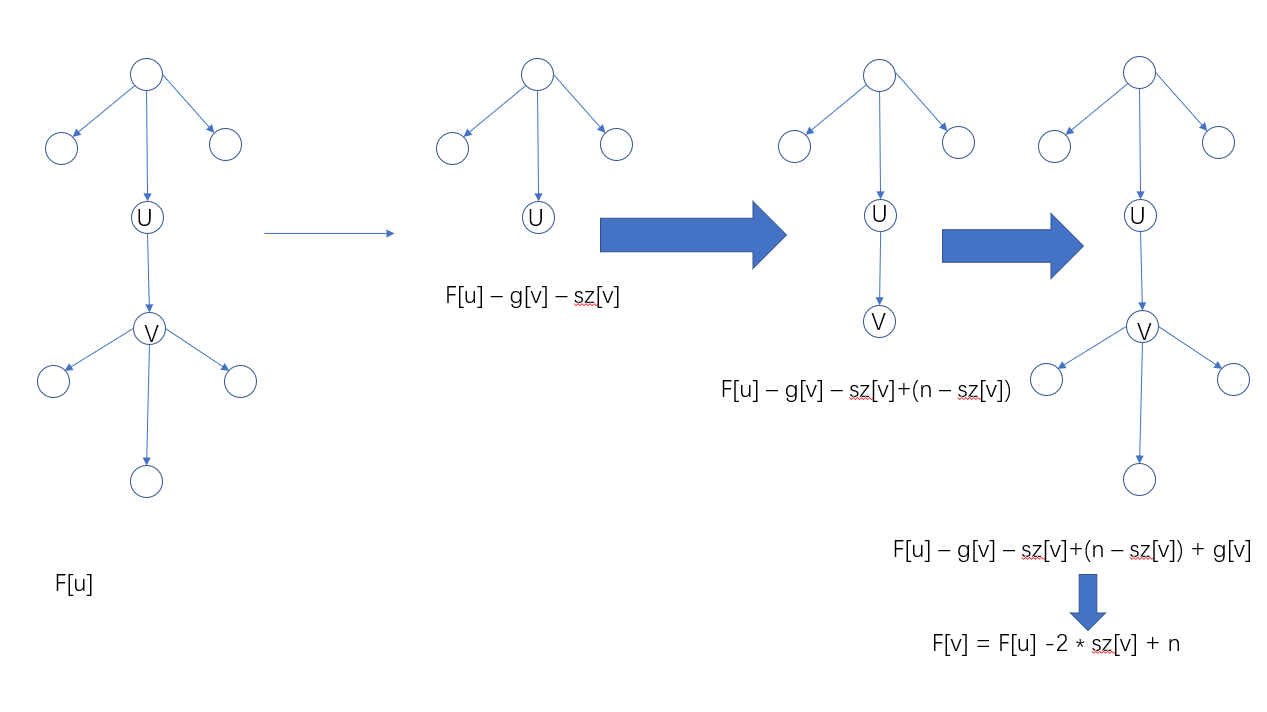
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define int long long
const int N = 2e6 + 10;
int h[N], e[N], ne[N], idx;
int death[N], sz[N], f[N];
int n;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs1(int u, int father)
{
sz[u] = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs1(v, u);
death[v] = death[u] + 1;
sz[u] += sz[v];
}
}
void dfs2(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
f[v] = f[u] - 2 * sz[v] + n;
dfs2(v, u);
}
}
signed main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs1(1, -1);
for(int i = 1; i <= n; i ++) f[1] += death[i];
dfs2(1, -1);
int maxx = 0, id;
for(int i = 1; i <= n; i ++)
if(f[i] > maxx) maxx = f[i], id = i;
cout << id << endl;
}
2.3 4381. 翻转树边
题意
$\space\space\space\space\space$ 给定一棵单向边的树 我们可以翻转边的方向进而使边可以通行 求点到其余所有点均抵达的前提下 翻转数量最少的数量
分析
$\space\space\space\space\space$ 与上题类似 也是换根dp 我们将原先方向直达的边权设置为0 反之设置为1 然后由上题的分析可得
$$ f[v] = f[u] + (w[i] == 1 ? -1 : 1)$$
源码
#include<iostream>
#include<cstring>
#include<algorithm>
#define int long long
using namespace std;
const int N = 2e6 + 10, INF = 1e18;
int f[N], g[N], depth[N];
int h[N], e[N], ne[N], w[N], idx;
int cnt[N];
int n;
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs_d(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs_d(v, u);
g[u] += g[v] + w[i];
}
}
void dfs_u(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
f[v] = f[u] + (w[i] == 1 ? -1 : 1);
dfs_u(v, u);
}
}
signed main()
{
memset(h, -1, sizeof h);
cin >> n;
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a, b, 0), add(b, a, 1);
}
dfs_d(1, -1);
f[1] = g[1];
dfs_u(1, -1);
int minn = INF;
for(int i = 1; i <= n; i ++) minn = min(f[i], minn);
cout << minn << endl;
for(int i = 1; i <= n; i ++)
if(f[i] == minn) cout << i << " ";
}
2.4 P3047 [USACO12FEB]Nearby Cows G
题意
$\space\space\space\space\space$ 给你一棵 n个点的树,点带权,对于每个节点求出距离它不超过 k 的所有节点权值和$m_i$
分析
$\space\space\space\space\space$ 考虑换根dp
f[N][M]; //以该点为中心距离不拆过k的范围的权值和
d[N][M]; //向下的深度的权值和
状态转移
d[u][j] += d[v][j - 1] 子节点更新父节点 自底向上递归
容斥思想 略证
f[v][j] = f[u][j - 1] + (d[v][j] - d[v][j - 2]) 父节点更新子节点 自顶向下 所以先转移在递归 并且 根节点的f[root][j] == d[root][j]
源码
#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int N = 2e5 + 10, mod = 1e9 + 7, M = 30;
int h[N], e[N], ne[N], w[N], idx;
int sum[N];
int n, m;
bool not_root[N];
int ans;
int f[N][M]; //以该点为中心距离不拆过k的范围的权值和
int d[N][M]; //向下的深度的权值和
/*
d[u][j] += d[v][j - 1] 子节点更新父节点 自底向上递归
f[v][j] = f[u][j - 1] + d[v][j] - d[v][j - 2] 父节点更新子节点 自顶向下 所以先转移在递归 并且 根节点的f[root][j] == d[root][j]
*/
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs_1(int u, int father)
{
for(int i = 0; i <= m; i ++) d[u][i] = w[u]; //初始化
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs_1(v, u);
for(int i = 1; i <= m; i ++) d[u][i] += d[v][i - 1];
}
}
void dfs_2(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
for(int j = 1; j <= m; j ++)
{
if(j >= 2) f[v][j] += f[u][j - 1] - d[v][j - 2]; //小容斥
else f[v][j] += d[u][j - 1];
}
dfs_2(v, u);
}
}
signed main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
not_root[b] = true;
}
for(int i = 1; i <= n; i ++) cin >> w[i];
int root = 1;
while(not_root[root]) root ++;
dfs_1(1, -1);
for(int i = 1; i <= n; i ++)
for(int j = 0; j <= m; j ++)
f[i][j] = d[i][j]; //值转移
dfs_2(1, -1);
for(int i = 1; i <= n; i ++) cout << f[i][m] << endl;
}
2.5 CF708C Centroids
题意
$\space\space\space\space\space$ 给定一颗树 你有一次将树改造的机会 改造的意思是删去一条边 再加入一条边 保证改造后还是一棵树 请问有多少点可以通过改造 成为这颗树的重心 (如果以某个点为根,每个子树的大小都不大于$\dfrac{n}{2}$ 则称某个点为重心)
分析
$\space\space\space\space\space$ 如果一个点是重心 不操作 否则该点一定有一个大于$\dfrac{n}{2}$ 的子树且只有一个 我们的操作就是在这样一个最大子树中 判断能否通过转移某个子节点的子树 使得该最大子树和转移的子树都满足 $\leq \dfrac{n}{2}$ 即可 我们用sz表示每个节点的子树大小 d1 d2 分别记录每个点由子节点转移来的最大和次大子树的根节点编号 我们用f1 f2 来表示该节点向下 向上的子树中可以操作的最大上限 即$\leq \dfrac{n}{2}$ 的最值 最后进行判断即可 我们用f2的目的是在子树遍历的时候我们为了避免成环 只向下进行搜索 所以导致向上的更新是个空白 而在由父节点更新子节点的最值时候 会出现父节点的最值恰好由子节点转移而来 所以需要次大值更新
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e6 + 10;
int h[N], e[N], ne[N], idx;
int sz[N], pre[N], d1[N], d2[N]; // sz maxsz 子树大小 d1 d2 记录该点的最大子树和次大子树的所属节点
int n;
int f1[N], f2[N], ans[N]; //向下 向下 满足 <= n / 2的最大可操作的值(子树的大小)
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs_1(int u, int father) //先更新子节点内的信息
{
sz[u] = 1;
f1[u] = f2[u] = 0;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs_1(v, u); //需要用子节点更新父节点 所以自底向上 选择先递归在更新
sz[u] += sz[v]; //统计以u为节点的子树大小
f1[u] = max(f1[u], f1[v]); // 找到所有子树里面最大可操作的范围
//对每个u节点 找到以u为根节点的最大子树和次大子树
if(sz[v] >= sz[d1[u]]) d2[u] = d1[u], d1[u] = v;
else if(sz[v] > sz[d2[u]]) d2[u] = v;
}
if(sz[u] <= n / 2) f1[u] = sz[u]; //如果该节点的子树大小小于 n / 2则选择整个子树
//否则就是不选整个子树 在遍历其的子节点选择整个子节点
}
void dfs_2(int u, int father) //在往上走 更新父节点上面的信息
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
if(n - sz[v] <= n / 2) f2[v] = n - sz[v]; // 如果 以v节点的父节点u的子树和 <= n / 2 我们就全选
else if(v != d1[u]) f2[v] = max(f2[u], f1[d1[u]]); // 否则在大于的时候 我们需要判断 最大子树的来源是否是v 不是的话 用最大值更新
else f2[v] = max(f2[u], f1[d2[u]]);//否则用次大值更新
dfs_2(v, u);
}
//如过以u节点向上的子树大于u节点向下的最大子树 那么我们判断>= n / 2的情况只能在上方
if(n - sz[u] > sz[d1[u]]) ans[u] = (n - sz[u] - f2[u] <= n / 2); //父节点
else ans[u] = (sz[d1[u]] - f1[d1[u]] <= n / 2); // 否则就是在下方
}
int main()
{
cin >> n;
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
dfs_1(1, -1);
dfs_2(1, -1);
for(int i = 1; i <= n; i ++) cout << ans[i] << " ";
}
2.6P6419 [COCI2014-2015#1] Kamp
题意
$\space\space\space\space\space$ 给你一棵树 有K个人 如果在第 i 个点举行聚会 司机最少需要多少时间把 K 个人都送回家 (ps 一次同时载所有人 而不是一人一送)
分析
$\space\space\space\space\space$ 考虑换根dp 我们将所有需要涉及的状态表示出来 以及u -> v的转移表示出来
f[u] 表示以u为根节点的子树中将子树内的所有人送完并回u的代价
g[u] 表示u子树外的人送完花费的代价
d1[u], d2[u] 表示以u为根节点的子树中的最长路 次长路
up[u] 表示以u为根节点的子树外的最大代价
对于每个遍历的每个点 我们知道 ans[i] = f[i] + g[i] - max(d1[i], up[i])
考虑u - > v转移
f[u] += f[v] + 2 * (w[u -> v])(v 是u的所有儿子节点)
(因为 v是u的儿子节点 那么g[v]的范围一定比g[u]大 (容斥))
对于g的转移我们需要讨论两个方面
1.如果v子树中有人 g[v] = g[u] + (f[u] - f[v]) v点外的所有代价 包括u点外的所有代价
以及同属一个u子树中的不是v子树的代价
2.如果对于u的子节点v中没有人居住 需要加上 2 * (w[u - > v])
解释 我们需要的操作是从u -> v也就是用u节点更新v节点 而对于v子树中只要存在关键点
他走到u点即对f[u]的贡献 一定是先经过v点 然后走s[u -> v]到的u点 也就是只要存在关键点来说
它的f[u] - f[v] 就包含了从u - >v的差价的代价 所以我们可以直接更新 而对于v子树没有关键点
则u- >v的路径我们需要单独加上
O(u)
|
O(v)
/ \
(关键点)O O(关键点) f[u] = f[v] + w[u -> v] ->>>> f[u] - f[v] = w[u - > v]
也就是有关键点 包含了u->v的路径 我们不做处理 反之我们需要加上该路径的权值
源码
#include<iostream>
#include<cstring>
#define int long long
using namespace std;
const int N = 1e6 + 10;
int h[N], e[N], ne[N], w[N], idx;
int sz[N], f[N], g[N];
int d1[N], d2[N], up[N], pre[N];
int n, m;
bool not_root[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs_1(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs_1(v, u);
int dist = d1[v] + w[i];
sz[u] += sz[v];
if(sz[v])//如果该子树有关键点 进行更新
{
f[u] += f[v] + 2 * w[i];
if(dist >= d1[u]) d2[u] = d1[u], d1[u] = dist, pre[u] = v;
else if(dist > d2[u]) d2[u] = dist;
}
}
}
void dfs_2(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
if(m - sz[v]) //如果子树外有关键点 进行更新
{
g[v] = g[u] + (f[u] - f[v]);
if(!sz[v]) g[v] += 2 * w[i]; //如果子树没有关键点 需要单独加上u - > v的路径
//维护up路径的更新
if(pre[u] == v) up[v] = max(up[u], d2[u]) + w[i];
else up[v] = max(d1[u], up[u]) + w[i];
}
dfs_2(v, u);
}
}
signed main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i < n; i ++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
not_root[b] = true;
}
for(int i = 1; i <= m; i ++)
{
int x;
cin >> x;
sz[x] ++; //对关键点进行标记
}
int root = 1;
while(not_root[root]) root ++;
dfs_1(root, -1);
dfs_2(root, -1);
for(int i = 1; i <= n; i ++) cout << g[i] <<" ";
// for(int i = 1; i <= n; i ++) cout << f[i] + g[i] - max(up[i], d1[i]) << endl;
}
3.1 1074. 二叉苹果树
题意
$\space\space\space\space\space$ 给定一棵树 每个树枝上有权值 要求仅仅保留k个树枝 使得权值最大
分析
$\space\space\space\space\space$ 如果没有树形结构的限制 显然这是一个背包问题 那么转移到树上就是一个典型的树上背包问题 考虑树上背包问题
f[u][k] 表示以u为根节点的子树中 选择k条边的最值
自底向上更新 对每一个子节点v看做一个组 对组内元素选择1-> sz[v]选择 进行更新即可
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110, M = N * 2;
int n, m;
int h[N], w[M], e[M], ne[M], idx;
int f[N][N];
int sz[N];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs(int u, int father)
{
sz[u] = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
sz[u] += sz[v];
for(int j = m; j >= 0; j --) //枚举体积
for(int k = 0; k <= min(sz[v], j - 1); k ++)//枚举可以选择的范围
f[u][j] = max(f[u][j], f[u][j - k - 1] + f[v][k] + w[i]);//需要注意的是 因为我们是枚举边 所以必须有一个边是返回到u节点的边
}
}
int main()
{
memset(h, -1, sizeof h);
memset(f, -1, sizeof f); //在体积恰好为j的时候的最值 记得初始化为极值
cin >> n >> m;
for(int i = 1; i < n; i ++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
for(int i = 1; i <= n; i ++) f[i][0] = 0; //更新初始的状态
dfs(1, -1);
cout << f[1][m] << endl;
}
3.2 P1273 有线电视网
题意
$\space\space\space\space\space$ 给定一个树 边有边权(即花费的代价) 点有点权 即盈利 写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。
分析
$\space\space\space\space\space$
源码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 3010;
typedef long long LL;
int n, m;
int h[N], e[N], ne[N], w[N], idx;
int val[N], sz[N];
int f[N][N]; //表示以i为根的子树中 选择j个用户的最大收益
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs(int u,int father)
{
if(u > n - m) //构建点权
{
f[u][1] = val[u];
sz[u] = 1;
return ;
}
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u); //子树的大小
sz[u] += sz[v];
for(int j = sz[u]; j >= 0; j --) //枚举体积
for(int k = 1; k <= sz[v]; k ++) //枚举可选的可能
if(j - k >= 0) f[u][j] = max(f[u][j], f[u][j - k] + f[v][k] - w[i]);
}
}
int main()
{
cin >> n >> m;
int t = n - m;
memset(h, -1, sizeof h);
memset(f, -0x3f, sizeof f); //选择恰好j个用户的最大收益 记得初始化为极值
for(int i = 1; i <= n; i ++) f[i][0] = 0; //更新初始状态
for(int i = 1; i <= t; i ++)
{
int k;
cin >> k;
while(k --)
{
int b, c;
cin >> b >> c;
add(i, b, c);
}
}
for(int i = t + 1; i <= n; i ++) cin >> val[i];
dfs(1, -1);
int ans = 0;
for(int i = 1; i <= n; i ++)
if(f[1][i] >= 0) ans = max(ans, i);
cout << ans << endl;
}
3.3 P2014 [CTSC1997] 选课
题意
$\space\space\space\space\space$ 给定一个树形依赖的选课方式 每个点有点权 求选择m门课的最大学分
分析
$\space\space\space\space\space$ 考虑树上背包 需要注意的是 本题的依赖关系可能不仅仅是一个树 而是一个森林 对于一个森林 我们构建一个虚拟原点0 用来连接所有的森林 成为一棵树
f[u][k]表示以u为根节点 选择k门课的最大学分
因为有初始0节点的设置 最后输出 f[0][m + 1]
转移方程与上述题类似 略
源码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 2e3 + 10;
int h[N], e[N], ne[N], w[N], idx;
int f[N][N];
int n, m;
int ans;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int father)
{
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
for(int j = m + 1; j >= 1; j --)
for(int k = 0; k < j; k ++)
f[u][j] = max(f[u][j], f[u][j - k] + f[v][k]);
}
}
int main()
{
memset(h, -1, sizeof h);
cin >> n >> m;
for(int i = 1; i <= n; i ++) //人为规定方向 单向建图即可
{
int b, c;
cin >> b >> c;
add(b, i); //b是先修课程 如果为0我们直接另0位最终的虚拟根节点
f[i][1] = c;
}
dfs(0, -1);
cout << f[0][m + 1] << endl;
}
3.4 P3698 [CQOI2017]小Q的棋盘
题意
$\space\space\space\space\space$ 给定一棵树 计算走k步最多能经过多少个不同的节点
分析
$\space\space\space\space\space$ 首先 我们的第一眼思路是f[u][k]从u点出发走k步走过的最多节点个数 但显然这不正确 因为我们不能类似于二叉苹果树的选择 此处我们是实际的行走 即从u的一个子树$v_1$ - >另一个子数$v_2$我们需要花费代价回到u点在进行行走 所以我们的实际定义状态为 f[u][k][0/ 1]
n, m 点数 可走的步数
f[u][j][0/ 1] 表示以u为根节点的子树 走j不 并0 (不回到起点 ) 1(回到起点)
f[u][j][1] = max(f[u][j][1], f[u][j - t][1] + f[v][t - 2][1])
f[u][j][0] = max(f[u][j][0], f[u][j - t][1] + f[v][t - 1][0], f[u][j - t][0] + f[v][t - 2][1])
$\space\space\space\space\space$ 其次 本题也可以用贪心求解 len 为最长链
ans = min(n, len + ((m - $\frac{len - 1}{2}$)) 即除了走最长链还能走的话 剩下的步数只能多走一半的点(来回计算双倍)
源码
/*
n, m 点数 可走的步数
f[u][j][0/ 1] 表示以u为根节点的子树 走j不 并0 (不回到起点 ) 1(回到起点)
f[u][j][1] = max(f[u][j][1], f[u][j - t][1] + f[v][t - 2][1])
f[u][j][0] = max(f[u][j][0], f[u][j - t][1] + f[v][t - 1][0], f[u][j - t][0] + f[v][t - 2][1])
贪心
len 为最长链
ans = min(n, len + ((m - (len - 1)) / 2)) 即除了走最长链还能走的话 剩下的步数只能多走一半的点(来回计算双倍)
*/
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1010;
int f[N][N][2];
int n, m;
int h[N], e[N], ne[N], idx;
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u, int father)
{
f[u][0][1] = f[u][0][0] = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
for(int j = m; j >= 0; j --)
{
for(int t = 0; t <= j; t ++)
{
int s1 = 0, s2 = 0;
if(t >= 1) s1 = f[u][j - t][1] + f[v][t - 1][0];
if(t >= 2) s2 = f[u][j - t][0] + f[v][t - 2][1];
f[u][j][0] = max(f[u][j][0], max(s1, s2));
if(t >= 2) f[u][j][1] = max(f[u][j][1], f[u][j - t][1] + f[v][t - 2][1]);
}
}
}
}
int main()
{
cin >> n >> m;
m = min(m, 2 * n - 2); //m 有上限限制 最多为2 * (n - 1) 在多便没有意义
memset(h, -1, sizeof h);
memset(f, -0x3f, sizeof f); //本题同样为恰好问题 记得初始化极值
for(int i = 1; i < n; i ++)
{
int a, b;
cin >> a >> b;
add(a + 1, b + 1), add(b + 1, a + 1);
}
dfs(1, -1);
int ans = 0;
cout << f[1][m][0] << endl;
}
3.5 P3177 [HAOI2015] 树上染色
题意
$\space\space\space\space\space$ 有一棵点数为 n 的树,树边有边权。给你一个在 0 ∼ n 之内的正整数k 你要在这棵树中选择 k 个点 将其染成黑色 并将其他 的 n - k 个点染成白色 将所有点染色后 你会获得黑点两两之间的距离加上白点两两之间的距离的和的受益 问受益最大值是多少。
分析
$\space\space\space\space\space$ 本题对于任意相同颜色两点的距离求和 不便于求解 我们可以退而求其次 计算此种方式分配的路径和 即根据分配方式的选择直接计算路径 进而转化为树上背包问题
其次 我们便可以定义转移方程 f[u][k] = max(f[u][j - k] + f[v][k] + val) val代表此种分配的路径和
其中val = (k * (m - k) + (sz[v] - k) * (n - sz[v] - m + k) ) * w[i];
源码
/*
本题对于任意相同颜色两点的距离求和 不便于求解 我们可以退而求其次 计算此种方式分配的路径和
即根据分配方式的选择直接计算路径 进而转化为树上背包问题
其次 我们便可以定义转移方程 f[u][k] = max(f[u][j - k] + f[v][k] + val) val代表此种分配的路径和
*/
#include<iostream>
#include<cstring>
#include<algorithm>
#define int long long
using namespace std;
#define endl '\n'
const int N = 2010, M = 4010;
int h[N], ne[M], e[M], w[M], idx;
int f[N][N], sz[N];
int n, m;
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
void dfs(int u, int father)
{
f[u][0] = f[u][1] = 0;
sz[u] = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
if(v == father) continue;
dfs(v, u);
sz[u] += sz[v];
for(int j = min(sz[u], m); j >= 0; j --) //枚举体积
{
for(int k = 0; k <= min(j, sz[v]); k ++) //枚举每个子树可选择的上限
{
if(f[u][j - k] == -1) continue; //如果他不合法
int val = (k * (m - k) + (sz[v] - k) * (n - sz[v] - m + k) ) * w[i]; //计算此种方式分配的路径和
f[u][j] = max(f[u][j], f[u][j - k] + f[v][k] + val); //转移方程
}
}
}
}
signed main()
{
ios :: sync_with_stdio(0); cin.tie(0); cout.tie(0);
memset(h, -1, sizeof h);
memset(f, -1, sizeof f);
cin >> n >> m;
for(int i = 1; i < n; i ++)
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c), add(b, a, c);
}
dfs(1, -1);
cout << f[1][m] << endl;
}
3.6 CF815C Karen and Supermarket
题意
$\space\space\space\space\space$ 给你一个有依赖的优惠券树 每个优惠券可以使用也可以不使用 求在最多m的金钱下购买物品的最值
分析
$\space\space\space\space\space$ 考虑树上分组背包
f[u][k][0/1]表示以u为根节点的子树中 选择k个物品 其中u节点不用/用优惠券的最少花费
状态转移
f[u][j + k][0] = min(f[u][j + k][0], f[u][j][0] + f[v][k][0]);
f[u][j + k][1] = min(f[u][j + k][1], f[u][j][1] + f[v][k][0]);
f[u][j + k][1] = min(f[u][j + k][1], f[u][j][1] + f[v][k][1]);
源码
#include<iostream>
#include<cstring>
#include<algorithm>
#define int long long
#define endl '\n'
using namespace std;
const int N = 5010;
int f[N][N][2];
int sz[N];
int n, m;
int e[N], ne[N], h[N], w[N], idx;
int a[N], b[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
void dfs(int u)
{
f[u][0][0] = 0;
f[u][1][0] = a[u];
f[u][1][1] = a[u] - b[u];
sz[u] = 1;
for(int i = h[u]; i != -1; i = ne[i])
{
int v = e[i];
dfs(v);
//ps 此题用涂板法 T了 需要刷刷板法 故sz的更新在后面进行
for(int j = sz[u]; j >= 0; j --)//枚举体积
{
for(int k = 0; k <= sz[v]; k ++)//枚举可选择的方案
{
f[u][j + k][0] = min(f[u][j + k][0], f[u][j][0] + f[v][k][0]);
f[u][j + k][1] = min(f[u][j + k][1], f[u][j][1] + f[v][k][0]);
f[u][j + k][1] = min(f[u][j + k][1], f[u][j][1] + f[v][k][1]);
}
}
sz[u] += sz[v];
}
}
signed main()
{
ios :: sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 1; i <= n; i ++)
{
int x;
if(i == 1) cin >> a[i] >> b[i];
else
{
cin >> a[i] >> b[i] >> x;
add(x, i);
}
}
memset(f, 0x3f, sizeof f);
dfs(1);
int id = 0;
for(int i = n; i >= 1; i --)
{
if(f[1][i][0] <= m || f[1][i][1] <= m)
{
id = i;
break;
}
}
cout << id << endl;
}
后记
$\space\space\space\space\space$ 很高兴你能看到这里 作为一个算法爱好者 对算法有着极其的热爱 我曾这样定义过热爱一词
我始终坚信 对某项工程抱有持之以恒的奋斗并为止而乐 才是最崇高的热爱
$\space\space\space\space\space$ 如果本文对你有所帮助 那便是本文最大的意义 同时 我也想说 对于每一个算法热爱者来说 永远要记得自己因何而出发 太多的艰难并不能阻止我们那颗为何出发的意志


%%%
%%%% xngg tql