高斯消元解线性方程组
枚举每一列c
- 枚举每一行找到当前行(包括当前行)下面的,当前列的绝对值最大的一个数。
- 将其绝对值最大的一行移到上面
- 将改行的第一个数变成1
- 将下面所有的行的当前列都清成0
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 110;
const double eps = 1e-8;
int n;
double a[N][N];
int gauss()
{
int c, r;
for(c = 0, r = 0; c < n; c ++)
{
int t = r;//存一下当前行
for(int i = r; i < n; i ++)
if(fabs(a[i][c] > fabs(a[t][c]))) //找到这一列最大的数,列不变找行
t = i;
if(fabs(a[t][c]) < eps) continue;//如果绝对值最大值都是零,不用处理下面的
for(int i = c; i <= n; i ++) swap(a[t][i], a[r][i]);//把这一行和r行交换,从第c列开始交换到第n列,相当于循环交换每一个元素
for(int i = n; i >= c; i --) a[r][i] /= a[r][c];//把当前行的首位变成1
for(int i = r + 1; i < n; i ++)//用当前行将下面所有的列消成0
{
if(fabs(a[i][c]) > eps)
{
for(int j = n; j >= c; j --)//从后往前,因为这也是消一行里的每一个元素
a[i][j] -= a[r][j] * a[i][c];
}
}
r ++;
}
if(r < n) //如果是唯一解,应该是完美阶梯型
{
for(int i = r; i < n; i ++)
if(fabs(a[i][n]) > eps) return 2; // 最后一行应该都是零,如果出现x != 0, 那么无解
return 1;// 有无穷多个解
}
for(int i = n - 2; i >= 0; i --)
for(int j = i + 1; j < n; j ++)
a[i][n] -= a[j][n] * a[i][j]; // 往回推,求a[i][n],a[i][n] = a[i][n] - 前面的系数 * 下面的a[i + 1][n]
return 0;
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)
for(int j = 0; j < n + 1;j ++)
cin >> a[i][j];
int t = gauss();
if(t == 2) puts("No solution");
else if(t == 1) puts("Infinite group solutions");
else
{
for(int i = 0; i < n; i ++)
{
if(fabs(a[i][n]) < eps) a[i][n] = 0;
printf("%.2lf\n", a[i][n]);
}
}
return 0;
}
高斯消元解异或线性方程组
- 左下角消0
- 枚举列
- 找第一个非零行
- 交换
- 把同列下面行消零(异或)
*判断3种情况 - 唯一解
- 秩<n
- 有矛盾 无解
- 无矛盾 无穷多解
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int a[N][N];
int n;
int gauss()
{
int c, r;
for(r = c = 0; c < n; c ++)//按列进行枚举
{
int t = r;
for(int i = r; i < n; i ++)//找到非零行,用t来存
if(a[i][c])
{
t = i;
break;
}
if(!a[t][c]) continue;//如果没有找到1,处理下一层
for(int i = c; i <= n; i ++) swap(a[t][i], a[r][i]);
for(int i = r + 1; i < n; i ++)//处理下面的行
{
if(a[i][c])//如果是1 则处理当前行
for(int j =c; j <= n; j ++)
a[i][j] ^= a[r][j];
}
r ++;
}
if(r < n)
{
for(int i = r; i < n; i ++)
if(a[i][n])
return 2;
return 1;
}
for(int i = n - 1; i >= 0; i --)
for(int j = i + 1; j < n; j ++)
a[i][n] ^= a[i][j] * a[j][n];//反推
return 0;
}
int main()
{
cin >> n;
for(int i = 0; i < n; i ++)
for(int j = 0; j < n + 1; j ++)
cin >> a[i][j];
int res = gauss();
if(res == 0)
{
for(int i = 0; i < n; i ++)
cout << a[i][n] << endl;
}
else if(res == 1) puts("Multiple sets of solutions");
else puts("No solution");
return 0;
}
组合数
1≤n≤100000 , 1≤b≤a≤2000, 递推 O(N2)
1≤n≤10000 , 1≤b≤a≤105, 预处理 O(NlogN)
1≤n≤20 , 1≤b≤a≤1018,1≤p≤105, 卢卡斯定理
(一)
Cba 是从a个苹果中选出b个苹果的总方案数:
分为两类:
1. 挑一个红苹果,选它,那只需要从剩下 a − 1 个苹果中挑 b − 1个
2. 挑一个红苹果,不选它,这是需要从剩下 a − 1 个苹果中挑 b 个
则Cba = Cb − 1a − 1 + Cba − 1
#include <iostream>
using namespace std;
const int N = 2010;
int c[N][N], mod = 1e9 + 7;
void init()
{
for(int i = 0; i < N; i ++)
for(int j = 0; j <= i; j ++)
if(!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
int main()
{
int n;
cin >> n;
init();
while(n --)
{
int a, b;
cin >> a >> b;
cout << c[a][b] << endl;
}
}
(二)
Cba = a!b!(a−b)!,即求 b!(a−b)! 的逆元(用快速幂)
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 100010, mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int a, int k, int p)
{
LL res = 1;
while(k)
{
if(k & 1) res = (LL) res * a % p;
k >>= 1;
a = (LL) a * a % p;
}
return res;;
}
int main()
{
int n;
cin >> n;
fact[0] = infact[0] = 1;
for(int i = 1; i < N; i ++)
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
while(n --)
{
int a, b;
cin >> a >> b;
cout << (LL)fact[a] * infact[b] % mod * infact[a - b] % mod << endl;
}
return 0;
}
(三)
卢卡斯定理
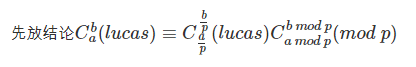
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
int qmi(int a, int k, int p)
{
int res = 1;
while(k)
{
if(k & 1) res = (LL) res * a % p;
k >>= 1;
a = (LL) a * a % p;
}
return res;
}
int C(int a, int b, int p)
{
if(b > a) return 0;
int res = 1;
// a!/(b!(a-b)!) = (a-b+1)*...*a / b! 分子有b项
for(int i = 1, j = a; i <= b; i ++, j --)
{
res = (LL) res * j % p;
res = (LL) res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if(a < p && b < p) return C(a, b, p);
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}
int main()
{
int n;
cin >> n;
while (n --)
{
LL a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
}
(四)
筛素数(1~5000)
求每个质数的次数
用高精度乘把所有质因子乘上
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 5010;
int primes[N];
int cnt;
int sum[N];
bool st[N];
void get_primes(int n)
{
for(int i = 2; i <= n; i ++)
{
if(!st[i]) primes[cnt ++] = i;
for(int j = 0; primes[j] <= n / i; j ++)
{
st[primes[j] * i] = true;
if(i % primes[j] == 0) break;
}
}
}
int get(int n, int p)
{
int res = 0;
while(n)
{
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t = 0;
for(int i = 0; i < a.size(); i ++)
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while(t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
int main()
{
int a, b;
cin >> a >> b;
get_primes(a);
for(int i = 0; i < cnt; i ++)
{
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p);
}
vector<int> res;
res.push_back(1);
for(int i = 0; i < cnt; i ++)
for(int j = 0; j < sum[i]; j ++)
res = mul(res, primes[i]);
for(int i = res.size() - 1; i >= 0; i --)
cout << res[i];
return 0;
}
满足条件的01序列
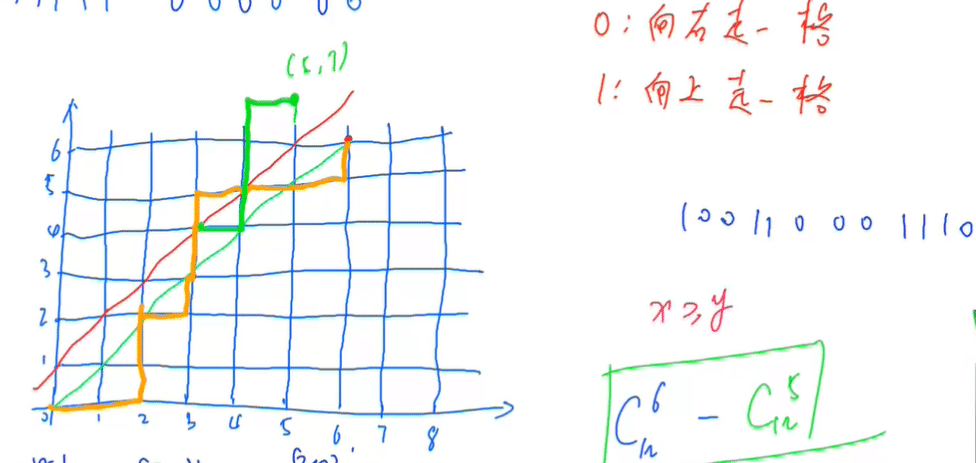
卡特兰数
Cn2n−Cn−12n=Cn2nn+1
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, mod = 1e9 + 7;
int qmi(int a, int k, int p)
{
int res = 1;
while(k)
{
if(k & 1) res = (LL)res * a % mod;
a = (LL)a * a % mod;
k >>= 1;
}
return res;
}
int main()
{
int n;
cin >> n;
int a = n * 2, b = n;
int res = 1;
for(int i = a; i > a - b; i --) res = (LL)res * i % mod;
for (int i = 1; i <= b; i ++ ) res = (LL)res * qmi(i, mod - 2, mod) % mod;
res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;
cout << res << endl;
return 0;
}
容斥原理
公式太多不好打,借鉴一下这篇题解
二进制表示状态:
将题目所给出的m个数可以看成是m位的二进制数,例如
当p[N]={2,3}时,此时会有01,10,11三种情况
而二进制的第零位表示的是p[0]上面的数字2,第1位表示p[1]上面的数字3
所以当i=1时表示只选择2的情况,当i=2(10)时,表示只选择3的情况,当i=3时,表示2和3相乘的情况
在过程中可以用标记变量t记录,可以按照t的值来选择是”+”还是“-”
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 20;
int n, m;
int p[N];
int main()
{
cin >> n >> m;
for(int i = 0; i < m; i ++)
cin >> p[i];
int res = 0;
for(int i = 1; i < 1 << m; i ++)//小于2^m
{
int t = 1;//选中集合对应质数的乘积
int s = 0;//选中的集合数量
//枚举m个质数
for(int j = 0; j < m; j ++)
{
if(i >> j & 1)
{
//如果t(已有的质数选法)乘上这个质数大于给定的数n,说明1∼n中的数不能被p整除
//此时直接返回break,跳过这个质数,(这里)不是很懂
if((LL)t * p[j] > n)
{
t = -1;
break;
}
s ++;
t *= p[j];
}
}
if(t != -1)
{
if(s % 2) res += n / t;
else res -= n / t;
}
}
cout << res << endl;
return 0;
}
博弈论
NIM游戏
先手必胜状态:先手操作完,可以走到某一个必败状态
先手必败状态:先手操作完,走不到任何一个必败状态
先手必败状态:a1 ^ a2 ^ a3 ^ … ^an = 0
先手必胜状态:a1 ^ a2 ^ a3 ^ … ^an ≠ 0
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int res = 0;
while(n --)
{
int x;
cin >> x;
res ^= x;
}
if(res) puts("Yes");
else puts("No");
return 0;
}
台阶-Nim游戏
如果先手时奇数台阶上的值的异或值为非0,则先手必胜,反之必败!
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int n;
cin >> n;
int res = 0;
for(int i = 1; i <= n ; i ++)
{
int x;
cin >> x;
if(i % 2) res ^= x;
}
if(res) puts("Yes");
else puts("No");
return 0;
}
集合-Nim游戏
1.Mex运算:
设S表示一个非负整数集合.定义mex(S)为求出不属于集合S的最小非负整数运算,即:
mes(S)=min{x};
例如:S={0,1,2,4},那么mes(S)=3;
2.SG函数
在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1,y2,····yk,定义SG(x)的后记节点y1,y2,····
yk的SG函数值构成的集合在执行mex运算的结果,即:
SG(x)=mex({SG(y1),SG(y2)····SG(yk)})
特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即 SG(G)=SG(s).
3.有向图游戏的和
设G1,G2,····,Gm是m个有向图游戏.定义有向图游戏G,他的行动规则是任选某个有向图游戏Gi,并在Gi上行动一步.G被称为有向图游戏G1,G2,·····,Gm的和.
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数的异或和,即:
SG(G)=SG(G1)xorSG(G2)xor···xor SG(Gm)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
using namespace std;
const int N = 110, M = 10010;
int n, m;
int s[N], f[M];//s存储的是可供选择的集合,f存储的是所有可能出现过的情况的sg值
int sg(int x)
{
if(f[x] != -1) return f[x];
unordered_set<int> S;
for(int i = 0; i < m; i ++)
{
int sum = s[i];
if(x >= sum) S.insert(sg(x - sum));
}
//选出最小的没有出现的自然数
for(int i = 0;; i ++)
{
if(!S.count(i))
return f[x] = i;
}
}
int main()
{
cin >> m;
for(int i = 0; i < m; i ++) cin >> s[i];
cin >> n;
memset(f, -1, sizeof f);
int res = 0;
for(int i = 0; i < n; i ++)
{
int x;
cin >> x;
res ^= sg(x);
}
if(res) puts("Yes");
else puts("No");
return 0;
}
拆分-Nim游戏
相比于集合-Nim,这里的每一堆可以变成小于原来那堆的任意大小的两堆
即a[i]可以拆分成(b[i],b[j]),为了避免重复规定b[i]>=b[j],即:a[i]>b[i]>=b[j]
相当于一个局面拆分成了两个局面,由SG函数理论,多个独立局面的SG值,等于这些局面SG值的异或和。
因此需要存储的状态就是sg(b[i])^sg(b[j])(与集合-Nim的唯一区别)
#include <iostream>
#include <algorithm>
#include <cstring>
#include <unordered_set>
using namespace std;
const int N = 110;
int n;
int f[N];
int sg(int x)
{
if(f[x] != -1) return f[x];
unordered_set<int> S;
for(int i = 0; i < x; i ++)
for(int j = 0; j <= i; j ++)
S.insert(sg(i) ^ sg(j));
for(int i = 0; ; i ++)
if(!S.count(i))
return f[x] = i;
}
int main()
{
cin >> n;
memset(f, -1, sizeof f);
int res = 0;
while(n --)
{
int x;
cin >> x;
res ^= sg(x);
}
if(res) puts("Yes");
else puts("No");
return 0;
}

