并查集算法详解

算法详解

维护类型

身为一个数据结构,我们的并查集,它的维护对象是我们的关注点.
并查集适合维护具有非常强烈的传递性质,或者是连通集合性质.

性质详解

传递性质

传递性,也就是具有传递效应的性质,比如说A传递给B一个性质或者条件,让B同样拥有了这个性质或者条件,那么这就是我们所说的传递性.

连通集合性质

连通集合性,和数学概念上的集合定义是差不多的, 比如说A和B同属一个集合,B和C同属一个集合,那么A,B,C都属于同一个集合.这就是我们所谓的连通集合性质.

算法步骤

一般来说数据结构算法,没有所谓的算法步骤,但是却有半确定的模块功能.

初始化操作

数据结构的初始化,通常都是有一个固定的模块,并查集也不例外.对于并查集而言,它的初始化,就是指向的父亲节点.

我们可以想象集合就是一个小圈子,而没一个小圈子都得有一个圈主,那么显然所以人都是围绕着圈主行动的.比如说Acwing这个大圈子中,yxc总裁就是我们的红太阳,圈主大人.

同属于一个集合的人们,显然每一个人的指向目标,显然都是这个圈子的圈主.

然而刚开始的时候,显然Acwing的成员们,在没有加入Acwing的时候,基本上都是素不相识的.因此呢,我们所有人肯定是都是属于自己的一个单人小圈子.自己显然就是自己这个小圈子的圈主.

综上所述,我们刚开始,每一个人的指向数组,也就是father数组,肯定都是指向自己.

合并操作

两个人最远的距离,是沉默,而Acwing这个大家庭,让你我们更加亲近.

海内存知己,天涯若比邻,网络世界的发展,Acwing网站的建立,沟通了身为程序员的你我他.

现在你成为了Acwing的一员,而小A同学也成为了Acwing的一员.

显然通过Acwing这个充满爱的大家庭,使得你和小A同学产生了联系,因此现在你和小A同学同属于一个名为Acwing的集合.

因为你和小A同学,需要建立一种联系,让全世界都知道,你和小A同学都来自富有爱心的网站Acwing大家庭,所以我们就需要用合并操作.

一个人的标签,就是一个人的指向数组,既然你想和小A同学缔结关系的话,那么你和小A同学的指向数组就需要开始变化了.

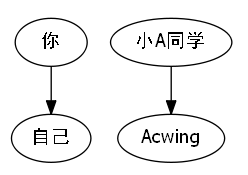
小A同学是Acwing的金牌元老,他的指示数组就是Acwing,那么身为新成员的你需要修改自己的指向数组,指向小A的同学.说明你和小A同学存在着上下级关系.

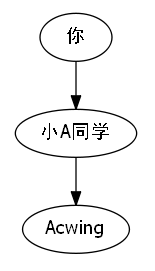
路径压缩

Acwing是一个充满温情的网站,上下级这种关系显然非常的不友好,那么我们不得不需要斩断这种关系.

你指向着小A同学,小A同学指向着Acwing.

这个大圈子的名字就叫做Acwing,显然小A同学和你同属于Acwing大圈子.

为了让上下级关系消失,我们不得不改变我们的集合指向方式.

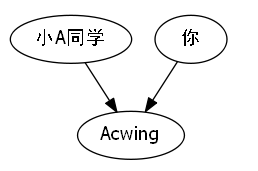
我们发现,如果说我们让所有Acwing成员,都指向Acwing这个大家庭的话,那么显然我们的上下级关系消失了,取而代之的则是我们的人人平等,互帮互助的友善关系.也就是我们的Acwing精神主旨之一.

Acwing精神不仅仅使得人与人之间更加友好,而且大大提高了我们的工作效率.

比如说如果说N个人,他们之间的关系统统都是上下级关系的话,那么显然我们的工作效率会大大降低.

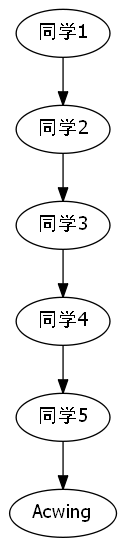
假如说同学6想要告诉Acwing网站的yxc总裁,一个地方有改进优化的建议,那么他需要不停地往上传递信息,效率是$O(n)$

但是如果我们按照人人平等,互帮互助的Acwing精神主旨之一,来进行编排的话,那么显然效率会乘坐火箭,大大提高.

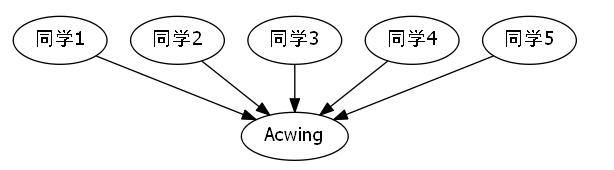
此时我们发现提出一个建议的效率,会大大提高,我们非常完美的处理,让效率成为了$O(1)$

题目选讲

原题连接

第一题

题目描述

有 $n$ 个同学（编号为 $1$ 到 $n$ ）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 $i$ 的同学的信息传递对象是编号为 $T_i$ 的同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息， 但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自 己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：

共$2$行。

第$1$行包含1个正整数 $n$ ，表示 $n$ 个人。

第$2$行包含 $n$ 个用空格隔开的正整数 $T_1,T_2,\cdots\cdots,T_n$ ，其中第 $i$ 个整数 $T_i$ 表示编号为 $i$ 的同学的信息传递对象是编号为 $T_i$ 的同学， $T_i \leq n$ 且 $T_i \neq i$ 。

输出格式：

$1$个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1：

5
2 4 2 3 1

输出样例#1：

3

说明

游戏的流程如图所示。当进行完第$ 3$ 轮游戏后， $4 $号玩家会听到 $2$ 号玩家告诉他自己的生日，所以答案为 $3$。当然，第 $3$ 轮游戏后，$ 2 $号玩家、 $3$ 号玩家都能从自己的消息来源得知自己的生日，同样符合游戏结束的条件。

对于 $30\%$的数据， $n \le 200$；

对于 $60\%$的数据， $n \le 2500$；

对于$ 100\%$的数据， $n \le 200000$。

解题报告

题意理解

每一轮,每一个人都会将自己手上所有的已知生日信息告诉别人,现在想要求出最少经过多少轮,你会知道你自己的生日信息.

性质分析

这道题目,直接了断地告诉我们,这道题目具有传递性质.因为我们的信息是传递的.

而且我们发现如果说一个人可以得到属于自己的生日信息的话,那么它肯定处于一个集合(环)之中,不然的话,它肯定无法得到自己的信息.

如下图所示.

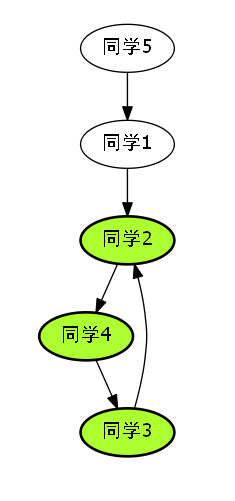
这道题目中,每一个就是一个节点,而每一个人手上拥有的信息,我们其实并不在意,因为我们只需要找到那个长度最小的环就好.

这是这道题目样例的解释,我们发现这道题目中,最小的环就是黄绿色部分.

算法分析

这道题目的核心要点,就是如何找到一个最小环.

这里的算法有很多种,比如说拓扑序,Tarjan,基环树等等,这里当然使用最好写的并查集算法,来Accept这道题目.

这道题目中的联通关系,其实题目中已经给出了,那就是我们的读入数据之中的第二行.

这里可以使用一个小技巧来统计最小环.

我们发现如果说,我们不使用路径优化的并查集算法,那么按照读入顺序,依次连通,会得出如下的图示.

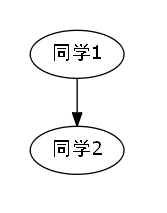
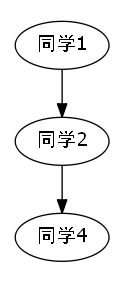
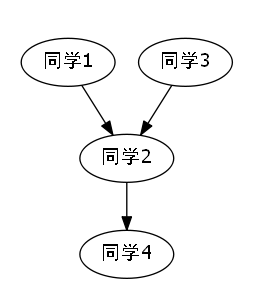
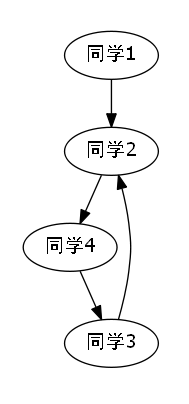
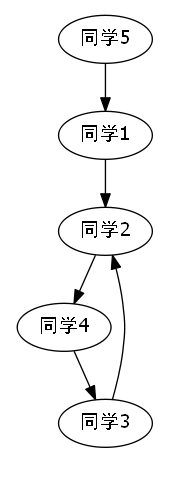
综上所述,我们成功地发现,我们每加入一条连通的关系,如果说在此刻正好发现,我们这个点和目标点,已经有关系了,那么显然我们构成了一个环,那么此时就是最小环

代码解说

#include <bits/stdc++.h>
using namespace std;
const int N=210000;//数据范围 
int fa[N],n,m,i,j,k,cnt,ans=1e9;//ans初始化 
int find(int x)
{
    cnt++;//统计最小环的长度 
    if (fa[x]==x)
        return x;
    else
        return find(fa[x]);
}
int main()
{
    ios::sync_with_stdio(false);
//  freopen("stdin.in","r",stdin);
//  freopen("stdout.out","w",stdout);
    cin>>n;
    for(int i=1; i<=n; i++)//必备并查集初始化 
        fa[i]=i;
    for(int i=1; i<=n; i++)
    {
        int x;
        cin>>x;
        cnt=0;//初始化 
        if (find(x)==i)//如果再一次遍历到了自己
            ans=min(ans,cnt);//更新答案 
        else
            fa[i]=x;//设置自己传递对象. 
    }
    cout<<ans;
    return 0;
}

第二题

题目描述

1920年的芝加哥，出现了一群强盗。如果两个强盗遇上了，那么他们要么是朋友，要么是敌人。而且有一点是肯定的，就是：

我朋友的朋友是我的朋友；

我敌人的敌人也是我的朋友。

两个强盗是同一团伙的条件是当且仅当他们是朋友。现在给你一些关于强盗们的信息，问你最多有多少个强盗团伙。

输入输出格式

输入格式：

输入的第一行是一个整数N$(2 \le N \le 1000)$，表示强盗的个数（从1编号到N）。 第二行M$(1 \le M \le 5000)$，表示关于强盗的信息条数。 以下M行，每行可能是F p q或是E p q$（1 \le p, q \le N）$，F表示p和q是朋友，E表示p和q是敌人。输入数据保证不会产生信息的矛盾。

输出格式：

输出只有一行，表示最大可能的团伙数。

输入输出样例

输入样例#1：

6
4
E 1 4
F 3 5
F 4 6
E 1 2

输出样例#1：

3

解题思路

题意理解

首先对于一道题目而言,题意是关键,这道题目的题意很简单,就是以上我加粗的黑体字,但是对于一道题目而言,题意往往内含大量条件&性质.

我朋友的朋友也是我的朋友.这句话的含义有两重含义.

1. 朋友的朋友们,和我都是一个阵营的.就比如说你的朋友是Acwing,那么Acwing的网友们,都和你是Acwing阵营的.
2. 朋友的敌人,和我关系不确定.比如说师娘显然和y总的桃花们是敌人,但是y总和他的桃花们关系是不确定的.师娘不要打我啊,y总太优秀了.(yxc女粉丝团)

我敌人的敌人也是我的朋友,这句话的含义同样有两重含义.

1. 敌人的敌人,和我是一个阵营的.这也好理解,共同的敌人,共同的利益,当然是一个小团体的.
2. 敌人的朋友,和我关系不确定比如说师娘显然追求者不止1个,但是y总和那群追求者的关系,也值得推敲深思.风水轮流转,师娘的微笑

条件分析

这道题目的分析,其实都在题意理解上面了,总而言之,我们的条件无非就是上面的两点.

1. 我朋友的朋友是我的朋友；

2. 我敌人的敌人也是我的朋友。

以及我们特别解释的两点.

思路分析

我们发现,如果说对于两人而言的话,假如说我们可以是朋友关系的话,那么我们立即将两人合并到一个集合即可.

然后最大可能的团伙数,其实就是固定确定好的最后团伙数.

代码展示

#include <bits/stdc++.h>
using namespace std;
const int N=1100;
int n,m,a,b,fa[N],f[N],vis[N];
char ch;
int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
void Union(int x,int y)//合并操作
{
    x=find(x);
    y=find(y);
    if(x==y)//本来就是一个团队的.
        return;
    fa[y]=x;//合并 
}
void work()
{
    if(ch=='F')//如果确定是朋友,那么马上合并
        Union(a,b);
    else
    {
        if(!f[a])
            f[a]=find(b);
        else
            Union(b,f[a]);//敌人不少于1个了
        if(!f[b])
            f[b]=find(a);//同上
        else
            Union(a,f[b]);//合并
    }
    return ;
}
void init()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1; i<=n; i++)//初始化
        fa[i]=i;
    while(m--)
    {
        cin>>ch>>a>>b;
        work();//处理
    }
    return ;
}
void out()
{
    int cnt=0;
    for(int i=1; i<=n; i++)
    {
        if (!vis[find(i)])//统计集合个数
        {
            vis[find(i)]++;
            cnt++;
        }
    }
    cout<<cnt;
    return ;
}
int main()
{
    init();
    out();
    return 0;
}