关于dijkstra能否求得负权边图单源最短路径

作者： 作者的头像   wanncy ,  2022-04-19 16:23:41 ,  所有人可见 ,  阅读 211

1


Dijkstra

我们知道 Dijkstra 是不能求带有负权边图的单源最短路径的，那么为什么呢：

你可能简单地认为是由于可能负权回路的存在导致的路径节点重走时路径会不断减小，但是本质上是这样的吗？

看这样一个图，

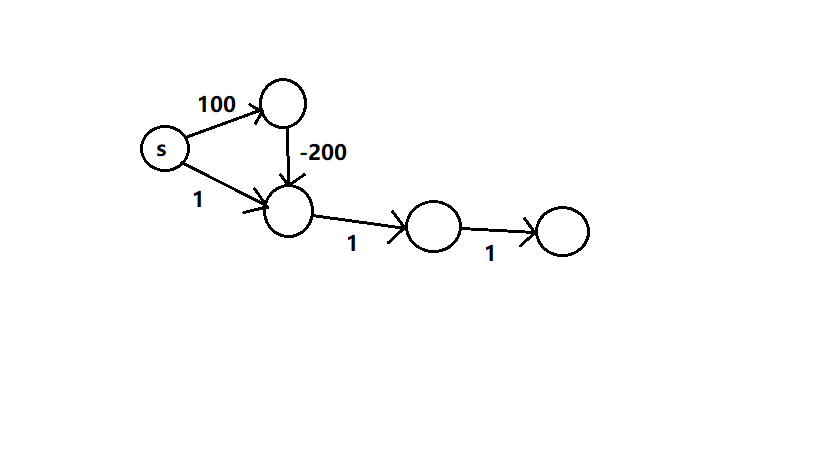
dijkstra

#include <iostream>
#include <cstring>

using namespace std;

// 因为 m 这里比较大，是稠密图，因此采用 邻接矩阵的存储方式
// dijkstra 需要：1. 图无负权边;
const int N = 510;
int g[N][N];
int dst[N], st[N];
int n, m;

void dijkstra() {
    // 从 1号节点开始
    dst[1] = 0;

    for (int i = 0; i < n; i++) {
        int t = -1;
        for (int j = 1; j <= n; j++) {
            if (!st[j] && (t == -1 || dst[j] < dst[t])) t = j;
        }
        st[t] = 1;
        // 更新现有最短距离
        for (int j = 1; j <= n; j++) dst[j] = min(dst[j], dst[t] + g[t][j]);
    }
    if (dst[n] >= 0x3f3f3f3f) {
        cout << -1;
    } else {
        cout << dst[n];
    }
}

int main() {
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    memset(dst, 0x3f, sizeof dst);

    int s, d, w;
    for (int i = 0; i < m; i++) {
        cin >> s >> d >> w;
        g[s][d] = min(g[s][d], w);
    }

    dijkstra();

    return 0;
}

我们使用标志位数组已经屏蔽了这样的重入节点，为啥还是应对不了这个case呢。

因为dijkstra本质是个贪心的算法，现有的最短路径都是建立在之前已经存在的最短路径基础上，这样就意味着dijkstra并不一定会完整地遍历到图中所有的边，会陷入局部最优，当然这种贪心不一定是坏的，对比于Bellman-Ford，在非负权路径下效率还是比较高且稳定的。

参考

0 评论