好烦的题！

中国剩余定理:
M = m1 * m2 * ... mk  
Mi = M / mi
M^-1表示Mi 模 mi 的逆元
回顾逆元: b * b^-1 同余 1 (mod m)
也就是说 Mi * x(表示M^-1) 同余 1 (mod mi)
->Mi * x + (-mi) * y = 1 
->Mi * x + (-mi) * y = gcd(Mi , -mi)
用这个扩展欧几里得求出x 也就是Mi的逆元
然后使用x = a1 * M1 * M1^-1 + a2 * M2 * M2^-1 ... ak * Mk * Mk^-1 来算出x 

题目:

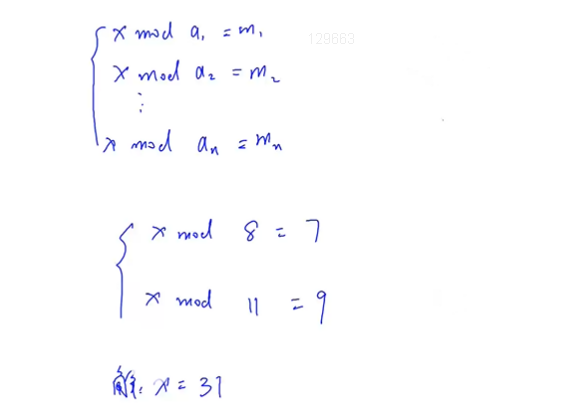
x mod a1 = m1
x mod a2 = m2 
...
x mod ak = mk
取前两个等式
k1 * a1 + m1 = k2 * a2 + m2
k1 * a1 - k2 * a2 = m2 - m1 
有解等价于gcd(a1 , a2) | m2 - m1

参考扩展欧几里得:a(x0 - b / d) + b(y0 + a / d) = gcd(a , b)是一组解
k1 , k2 所有解可以表示成
k1 = k1 + k * a2 / d
k2 = k2 + k * a1 / d 

因为 x = k1 * a1 + m1 , k1 = k1 + k * a2 / d 
那么x所有的解可以表示成 x = (k1 + k * a2 / d) * a1 + m1 
整理一下得
x = a1 * k + m1 + k * (a1 * a2 / d)
a1 * a2 / d 表示成 a1 和 a2得最小公倍数
所以:x = a1 * k + m1 + k * lcm(a , b)

设x0 = a1 * k + m1 ,a =  lcm(a , b) 
所以 x = x0 + k * a 
合并两个式子可以得到一个式子
合并n - 1个式子求得最后一个式子

若剩最后一个式子：x = x0 + k * a 可以表示为：x mod a 同余 x0 
求这个式子的最小正整数解
也就是求 x0 mod a 的正整数解